
- •Оглавление
- •Аналитические технологии
- •Формализация нейронных сетей
- •Принцип обучения искусственных нейронных сетей
- •Концепция обучения нейронной сети, предложенная Хэбом
- •Сбор данных для нейронной сети
- •Прикладные возможности нейронных сетей
- •Переобучение и обобщение
- •Персептрон
- •Алгоритм обратного распространения ошибки
- •Сигмоидальный нейрон
- •Нейрон типа «адалайн»
- •Инстар и оутстар Гроссберга
- •Нейрон типа wta (Winner Takes All)
- •08.10.2011 Модель нейрона Хэбба
- •Стохастическая модель нейрона
- •Стохастические алгоритмы обучения
- •Настройка числа нейронов в скрытых слоях многослойных сетей в процессе обучения
- •Алгоритмы сокращения
- •Конструктивные алгоритмы
- •Упрощенные алгоритмы расщепления
- •Радиальная базисная сеть
- •Вероятностные нейронные сети
- •Линейные нейронные сети
- •Обучение
- •Сети с самоорганизацией на основе конкуренции
- •12.11.2011 Модели ассоциативной памяти. Сети Хопфилда
- •Когнитивные карты
- •19.11.2011 Генетические алгоритмы Естественный отбор и генетическое наследование
- •Модель эволюции в природе, реализованная программно
- •Символьная модель простого генетического алгоритма
- •Работа простого генетического алгоритма
- •26.11.2011 Шима (Schema)
- •Применение аналитических технологий
- •03.12.2011
- •Бизнес-приложения
- •Программные реализации аналитических технологий
- •Список литературы
Линейные нейронные сети
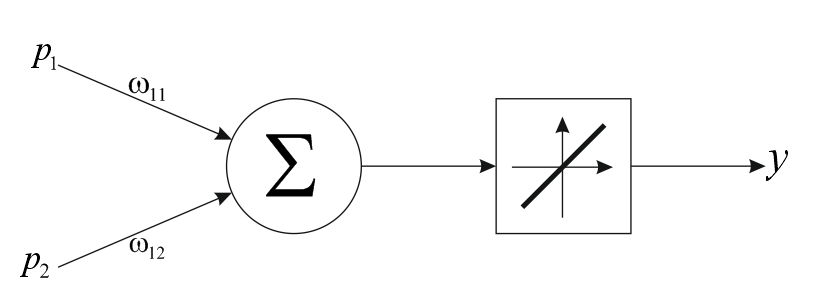
Рисунок 27 Линейная нейронная сеть
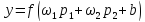
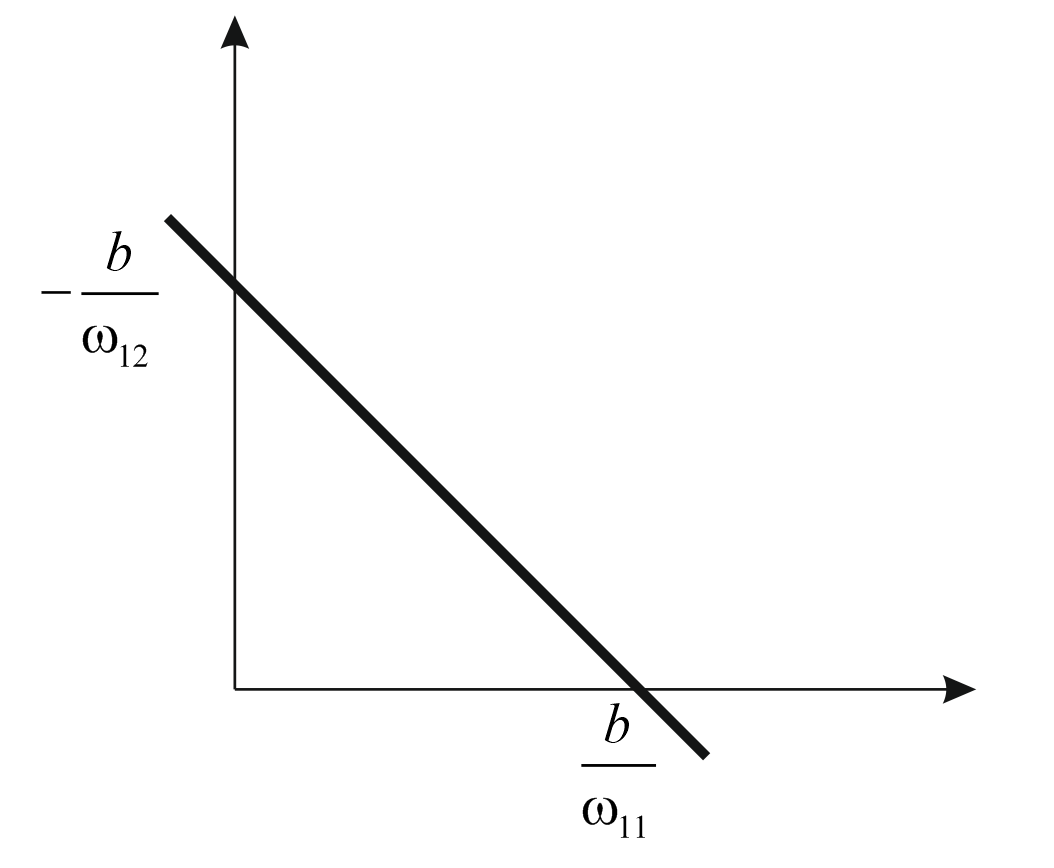
Рисунок 28 График линейной сети
Линейные сети по своей структуре аналогичны персептроным и отличаются лишь функцией активации.
Обучение
Для заданной линейной сети и соответствующим множествам вектором входа и целей можно вычислить вектор выхода сети и сформировать разность между векторами выхода и целевым вектором, который определяет некоторую погрешность обучения. Функция среднеквадратичной ошибки имеет вид:
 ,
где
,
где
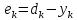
Для линейной нейронной сети используется правило обучения Видроу-Хоффа. Процесс обучения состоит в следующем. Сформируем частную производную по весам и смещением от квадрата погрешности на k-ой итерации.
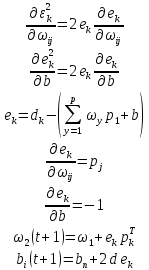
Сети с самоорганизацией на основе конкуренции
Основу самоорганизации нейронных сетей составляет закономерность, что глобальной упорядочение сети становится возможным в результате самоорганизации операций, независимо происходящих в различных локальных сегментах сети. В соответствии с поданными на вход сигналами осуществляется активация нейрона, который вследствие изменения значений синоптических весов адаптируется к поступающим обучающим выборкам.
Среди механизмов самоорганизации выделим 2:
Самоорганизация, основанная на ассоциативном правиле Хэбба;
Самоорганизация, основанная на конкуренции между нейронами на базе обобщенном правила Кохонена;
Рисунок 29 правило Кохонена
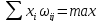
Для сетей с самоорганизацией, основу обучения которых составляет конкуренция между нейронами, обязательным является наличие связей для каждого нейрона со всеми компонентами входного вектора. При активации сети вектором X в конкурентной борьбе побеждает тот нейрон, веса которого в наименьшей степени отличаются от соответствующих компонентов этого вектора.
Для j-того нейрона-победителя соотношение:
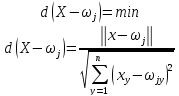
d-
расстояние между вектором X
и
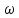 .
Вокруг нейрона-победителя образуется
топологическая окрестность. Все нейроны
в пределах этой окрестности подвергаются
адаптации по правилу Хопфилда:
.
Вокруг нейрона-победителя образуется
топологическая окрестность. Все нейроны
в пределах этой окрестности подвергаются
адаптации по правилу Хопфилда:
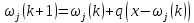
Алгоритм Кохоненапредполагает приписывание нейронам определенных позиций в произведении и связывание их с соседями на постоянной основе. В момент выбора победителя уточняются не только его веса, но и все его соседей, находящихся в ближайшей окрестности. В классическом алгоритме Кохонена функция соседства определяется так:
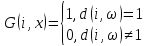
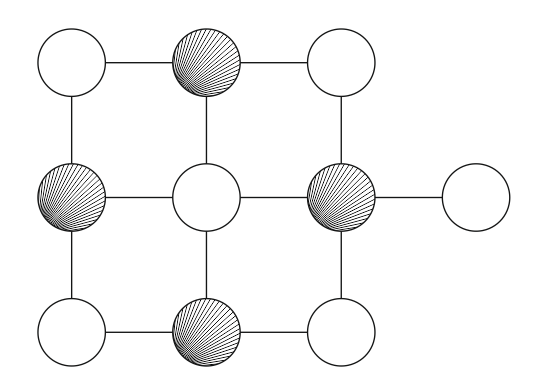
Рисунок 30 АЛгоритм Кохонена
В
этом выражении
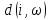 (расстояние
междуi-ым
нейроном и нейроном-победителем) –
расстояние, измеряемое в количестве
нейронов. Коэффициент 1 выступает в
качестве уровня соседства. Соседство
такого рода называется прямоугольным.
Другой тип соседства – соседства
гауссовского типа, где:
(расстояние
междуi-ым
нейроном и нейроном-победителем) –
расстояние, измеряемое в количестве
нейронов. Коэффициент 1 выступает в
качестве уровня соседства. Соседство
такого рода называется прямоугольным.
Другой тип соседства – соседства
гауссовского типа, где:
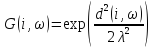 ,
где
,
где
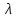 - определяет уровень соседства.
- определяет уровень соседства.
Степень
адаптации нейронов-соседей определяется
не только
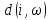 ,
но и уровнем соседства. В отличии от
соседства прямоугольного типа, где
каждый нейрон, находящийся в окрестности
победителя, адаптируется в равной
степени, при соседстве гаусовского типа
уровень адаптации отличается.
,
но и уровнем соседства. В отличии от
соседства прямоугольного типа, где
каждый нейрон, находящийся в окрестности
победителя, адаптируется в равной
степени, при соседстве гаусовского типа
уровень адаптации отличается.
Процесс самоорганизации предполагает определение победителя каждого этапа. При инициализации весов сети случайным образом, часть нейронов может оказаться в области правила, в котором отсутствуют данные или их количество ничтожно мало. Эти нейроны имеют мало шансов на победу и адаптацию своих весов, поэтому они остаются мертвыми. Для активации всех нейронов сети в алгоритме обучения необходимо предусмотреть учет побед каждого нейрона с использование либо соседства гауссовского типа, либо так называемого механизма утомления. Также используется механизм штрафов для самых активных нейронов.
