Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

умк_Цывис_Диф.уравнения_Ряды

.pdf

Скачиваний:

Добавлен:

18.05.2015

Размер:

5.68 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 225 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

Уравнение (14) – линейное дифференциальное уравнение первого порядка относительно переменной Z, которое можно интегрировать мето- дами, рассмотренными выше.

Отметим, что удобнее интегрировать уравнение Бернулли подста- новкой y = u(x) × s(x) .

Пример 5. Найти уравнение кривой, проходящей через точку А(0;1), если известно, что в каждой точке нормаль к кривой отсекает на оси абсцисс отрезок, равный квадрату расстояния от начала координат до этой точки.

Решение.		Пусть М(x,y) –	произвольная точка искомой		кривой
y = f (x) . Уравнение нормали к кривой y = f (x) в точке				M(x,y) имеет
вид Y - y =	−1	( X - x) . Полагая в последнем уравнении		Y = 0,	найдем
вид Y - y =	y¢(x)	( X - x) . Полагая в последнем уравнении		Y = 0,	найдем
	y¢(x)
абсциссу точки пересечения нормали и оси абсцисс в виде
		X = x + yy′ .
Тогда уз условия задачи получим уравнение
		x + yy¢ = x2 + y2	или y¢ - y = (x2 - x) y−1 .

Это уравнение

s(u¢ - u) + us¢ =			x2 - x

			us

u′ − u = 0,
	′	x2 − x
	uσ =			,
			uσ

Бернулли, поэтому

откуда

u′ - u = 0,

σdσ = (x2 − x)e−2 xdx,

y = u × s; y	′	′	′	и
		= u s + s u

u = ex ,

σ2 = −x2e−2 x + c.

Тогда y = u × s = ±ex × c - x2e−2 x или x2 + y2 = ce2 x , а так как кри-

вая проходит через точку А(0;1), то с =1. Следовательно, уравнение иско- мой кривой x2 + y2 = e2 x .

Уравнение Дарбу

Дифференциальное уравнение вида

M (x, y)dx + N (x, y)dy + P(x, y)(xdy - ydx) = 0 ,

где M(x,y) и N(x,y) – однородные функции порядка m, а P(x,y) – одно- родная функция порядка l (l ¹ m -1) , называется уравнением Дарбу.

Уравнение Дарбу всегда интегрируется в квадратурах, т.к. подстановка y = z × x (z – новая неизвестная функция) приводит к уравнению Бернулли

с неизвестной функцией x от независимой переменной z, причем послед- нее уравнение будет линейным, если l = m – 2, и уравнением с разделяю- щимися переменными, если N(x,y) = 0.


	y
Пример 6 . Решить уравнение		- y dx + (x -1)dy = 0 .
	x

Решение.

Запишем

данное

уравнение

виде

dx - dy + xdy - ydx = 0 , так как m = 0 и l = 0,

то это уравнение Дарбу,

тогда с помощью подстановки y = z·x,

получаем

dy = xdz + zdx;

xdy - ydx = x2dz ,

(

- z)dx + (x2 - x)dz = 0

– уравнение

или

z -

Бернулли относительно функции x ( z -

¹ 0 ).

= c(1 - z )2

Интегрируя, получим

+1 или

= c 1

+1.

Уравнение Риккати

Уравнение вида

y¢ = P(x) y2 + Q(x) y + R(x) , где правая часть –

квад-

ратичная функция от y

(R(x) ¹ 0) , называется уравнением Риккати.

Уравнение Риккати в общем случае не интегрируется в квадратурах,

но если y1 его частное решение, то подстановкой y = y

z –

новая не-

известная функция, оно приводится к линейному уравнению

z′ + (2P(x) y1 + Q(x))z = −P(x) .

Если известно одно частное решение

y1(x) , то заменой

y = y1(x) + z

уравнение Риккати сводится к уравнению Бернулли

и,

следовательно,

∫ f (x)dx + ∫j( y)dy = C

может быть решено в квадратурах.

Отметим, что уравнение Риккати

y¢ = Ay 2 + B

где А, В и С R, допускает частное решение вида y (x) =

, a Î R , если

алгебраическое уравнение Aa2 + (B +1)a + C = 0 относительно

имеет

действительные корни.

Уравнение Риккати вида y¢ = A	y2	+	y	+ C подстановкой y =		×u
					x
	x
			2x

приводится к уравнению с разделяющимися переменными. Уравнение Рик-

кати вида

y¢ = ay2 +

заменой

y =

сводится к однородному уравнению.

Пример 7.

Решить уравнение

y¢ + y2 =

Решение.

Это уравнение Риккати. Частное решение y (x) = −1 (еще

одно частное y =

). Тогда

y = z -

и получим z¢ -

= -z2 ,

умножим

на x2, получим

d (zx)

= 3zx - (zx)2 ;

u = zx .

Тогда

= u(3 - u)

или

u = (u - 3)cx3

и u = 3,

получим

z = c(zx - 3)x3 ; z =

y = z -

2cx3 +1

y =

Окончательно

(cx3

-1)x

Замечание 1.

Некоторые классы уравнений становятся линейными,

если x

–

функция,

а y

–

аргумент.

Так

нелинейное

уравнение

A( y) + ( B( y)x - C( y)) dy = 0 относительно y решается как линейное, от-


			dx
носительно x, – если его представить в виде
					dx	+ j( y) × x = f ( y) ,
						+ j( y) × x = f ( y) ,
					dy
где j( y) =	B( y)	;	f ( y) =	C( y)			.
где j( y) =		;	f ( y) =				.
	A( y)			A( y)

К линейным приводятся уравнения вида

f ¢( y) dy + f ( y) × a(x) = b(x) , dx

с помощью замены z = f(y). Например, уравнение Бернулли заменой z = y1– n приводится к линейному уравнению.

Пример 8. Найти решение уравнения ( y2 - 6x) y¢ + 2 y = 0 .

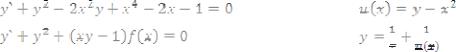
Решение. Это уравнение не является линейным, если считать иско- мой функцией y, но оно оказывается линейным, если искомая функция x, а

y – аргумент. Данное уравнение эквивалентно уравнению

′

− 6x = − y

2 yx

Уравнение Бернулли относительно функции x интегрируем, исполь-

зуя подстановку x = u × s, получим общее решение в виде

2x = y2 + cy3 .

Пример 9. С помощью замены переменных или дифференцирования

следующие уравнения привести к линейным и решить их.

xdx = (x2 − 2 y + 1)dy ;

2. (x + 1)( yy′ −1) = y2 ;

x(e

′

4. (x

′

sin y + 2x cos y =

2x − 2x

;

− y ) = 2 ;

−1) y

y(x) = ∫ y(t)dt + x + 1.

Ответы и указания: 1. x2 = 2 y + Ce2 y , подстановка x2 − 2 y + 1 = t ;

y2 = C(x + 1)2 − 2(x + 1) , замена y2 = t ;

x + Cx2 = e− y , замена

e y = t ;

4.cos y = (x2 −1)ln C(x2 −1) , замена cos y = t ;

5.y = 2ex −1.

Пример 10. Подобрать частное решение для уравнения Риккати.

1. x2 y′ + xy + x2 y2 = 4 ; y1 =

;

y′ − y2 − xy − x + 1 = 0 ; y1 = −1;

y′ − y2 + y sin x − cos x = 0 ; y1 = sin x ;

y′ + 2 y 2 −

= 0 ; y1 =

; y2

= −

;

5. 3y′ + y2 +

= 0 ; y1 =

;

y′ = 2xy + y2 = 5 − x2 ; y1 = x + 2 ;

7.y′ + 2 yex − y2 = e2x + ex ;

8.y′ = y2 − xy − x ; y1 = x + 1.

Пример 11. Преобразовать уравнение Риккати с помощью указан- ных подстановок и указать тип полученных уравнений.

1.		;	.


2.	;			.

3.	;					.


4.				;			.



5.		;					.


6.			;			.




7.					;	.

Ответы:

1. – уравнение с разделяющимися переменными.

2. – линейное уравнение.

3. – уравнение с разделяющимися переменными.

4. – уравнение Бернулли.

5. – уравнение Бернулли.

6. – уравнение Бернулли.

7. – уравнение Бернулли.

2.5. Уравнение в полных дифференциалах. Интегрирующий множитель

Если в дифференциальном уравнении

P(x, y)dx + Q(x, y)dy = 0

(1)

левая часть есть полный дифференциал некоторой функции u(x,y), то та- кое уравнение называется дифференциальным уравнением в полных диф- ференциалах. В этом случае дифференциальное уравнение (1) можно пред- ставить в виде

du(x, y) = 0 ,	(2)
а его общий интеграл
u(x, y) = c .	(3)

Отметим, что уравнение (1) особых решений не имеет.

Признак уравнения в полных дифференциалах устанавливается сле- дующей теоремой.

Теорема 1. Если функции P(x,y) и Q(x,y) непрерывны вместе с ча-

∂P ∂Q

стными производными ∂y и ∂x в некоторой односвязной области D,

то для того, чтобы уравнение (1) было уравнением в полных дифферен- циалах, необходимо и достаточно, чтобы выполнялось тождество

∂P ≡	∂Q .	(4)
∂y	∂x

Доказательство.

Необходимость. Пусть левая часть уравнения (1) есть полный диф- ференциал некоторой функции u(x,y). Тогда

P(x, y)dx + Q(x, y)dy = du(x, y) =			∂u dx +	∂u dy
			∂x	∂y
откуда и имеем	∂u
	∂u
P(x, y) =		,
P(x, y) =		,
	∂x			(5)
	∂u .			(5)
Q(x, y) =	∂u .
	∂y

Дифференцируя первое из равенств (5) по y, а второе по x, получим

∂P =	∂2u	;	∂Q =	∂2u	.

∂y	∂x∂y		∂x	∂y∂x
В силу равенства вторых смешанных производных, получаем тож-
дество (4).
Достаточность. Пусть в области D				справедливо тождество (4).
Покажем, что существует функция u(x,y) в области D такая, что
du(x, y) = P(x, y)dx + Q(x, y)dy .
Фиксируя y в первом уравнении (5) и интегрируя по x, получим
u(x, y) = ∫P(x, y)dx + ϕ( y) .						(6)

В (6) роль произвольной постоянной выполняет ϕ(y) – функция от y. Определим функцию ϕ(y) в равенстве (6), и тем самым найдем решение дифференциального уравнения (1). Для этого продиффиринцируем равенст-

во (6) по y и результат приравняем Q(x,y)

(второе уравнение (5)), получим

∂u

= ∫

∂P(x, y)

′

∂y

dx + ϕ

( y) = Q(x, y) .

Откуда

∂P(x, y)

′

(7)

ϕ ( y) = Q(x, y) − ∫

∂y

dx .

Левая часть равенства (7) зависит от

y. Докажем, что и правая часть

равенства (7) зависит только от y

(не зависит от

x). Дифференцируя пра-

вую часть (7) по x,

с учетом условия (4) получим

∂

∂Q

∂

Q(x, y)

− ∫ ∂Pdx =

−

∫

∂Pdx =

∂x

∂y

∂x

∂y

∂Q

∂

(∫ P(x, y)dx)

∂Q

∂P

∂x

−

∂x

−

∂y

= 0.

∂y

∂x

Так как производная по x тождественно равна нулю, то правая часть равенства (7) не зависит от x.

Интегрируя равенство (7) по y, получим


ϕ( y) = ∫ Q(x, y) − ∫	∂Pdx dy .
	∂y

Подставляя найденное значение ϕ(y)	в (6), получим

u(x, y) = ∫P(x, y)dx + ∫ Q(x, y) − ∫		∂Pdx dy
		∂y

это искомая функция, такая, что du(x, y) = P(x, y)dx + Q(x, y)dy .

Таким образом, в силу доказанной теоремы 1 решение дифференци- ального уравнения (1) строится следующим образом:

1.проверяем выполнение условия (4),

2.находим функцию u(x,y) по методу, изложенному при доказатель- стве достаточного условия теоремы 1,

3.общее решение уравнения (1) имеет вид u(x,y) = c.

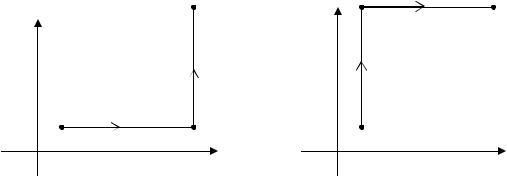
	Пример 1.		Решить уравнение
			(2xy + 3y2 )dx + (x2 + 6xy − 3y2 )dy = 0 .
	Решение.		В	данном	случае	P(x, y) = 2xy + 3y2	и
Q(x, y) = x2 + 6xy − 3y2 , тогда ∂Q(x, y) = 2x + 6 y и						∂P = 2x + 6 y . Таким об-
				∂x		∂y
разом	∂Q =	∂P , и, следовательно, левая часть данного уравнения является
	∂x	∂y
полным дифференциалом некоторой функции u(x,y), для которой имеем
			∂u = 2x + 3y2 ;		∂u = x2 + 6xy − 3y2 .
			∂x		∂y
	Из первого уравнения получим				u(x, y) = x2 y + 3xy2 + ϕ( y) . Для оп-

ределения ϕ(y) дифференцируем последнее равенство по y и приравнива-

ем к	∂u = x2 + 6xy − 3y2 , т.е.	∂u = x2 + 6xy +	∂ϕ = x2 + 6xy − 3y2 , откуда
	∂y	∂y	∂y

∂ϕ = −3y2 , т.е. ϕ( y) = − y3 , поэтому u(x, y) = x2 y + 3xy2 − y3 + C . Тогда ре-
∂y	1
	1
шение исходного уравнения имеет вид
x2 y + 3xy2 − y3 = C .

Замечание 1. Функцию u(x,y) можно определить по ее полному дифференциалу

du = M (x, y)dx + N (x, y)dy .

Вычислим криволинейный интеграл второго рода между некоторой фиксированной точкой (x0,y0) и точкой с переменными координатами (x,y) по любому пути:

( x, y)

u(x, y) = ∫ M (x, y)dx + N (x, y)dy .

( x0 , y0 )

Удобнее в качестве пути интегрирования брать ломаную, состав- ленную из двух звеньев, параллельных осям координат (рис. 1).

(x,y)	y	(x0,y)
		(x,y)
y

	x0, y0	(x,y0)
		(x,y0)		x0,y0
				x0,y0
0		x	0	x

Рис. 1

В этом случае имеем

	( x, y)
	u(x, y) = ∫	M (x, y)dx + N (x, y)dy =
	( x0 , y0 )
( x, y0 )	( x, y)	( x0 , y)	( x, y)
= ∫	M (x, y0 )dx + ∫ N (x, y)dy = ∫		N (x0 , y)dy + ∫ M (x, y)dx.
( x0 , y0 )	( x0 , y0 )	( x0 , y0 )	( x0 , y)

Замечание 2. Если дифференциальное уравнение (1) является диф- ференциальным уравнением в полных дифференциалах, т.е. справедливо условие (4), то общий интеграл дифференциального уравнения (1) можно записать в виде

x	y
∫ P(x, y)dx + ∫Q(x0 , y)dy = C		(8)
x0	y0
или
x	y
∫	P(x, y0 )dx + ∫Q(x, y)dy = C ,	(9)
x0	y0

где (x0,y0) – точка, принадлежащая области D.

Решение задачи Коши с начальными данными (x0,y0), принадлежа-

щими области D, и такими, что P2 (x0 , y0 ) + Q2 (x0 , y0 ) ¹ 0 , получается из общего интеграла (8) или (9) при С = 0.

x	y
∫	P(x, y)dx + ∫Q(x0 , y)dy = 0	(10)
x0	y0
или
x	y
∫ P(x, y0 )dx + ∫Q(x, y)dy = 0		(11)
x0	y0

причем это решение единственное.

На примере дифференциального уравнения рассмотрим два способа интегрирования.

Левая часть уравнения является полным дифференциалом некоторой функции u(x,y),т.к.

¶(x + y +1)

¶(x - y2 + 3)

=1.

¶y

¶x

1 способ:

∂u = x - C( y) ;

∂u = x + y +1;

;

¶x

¶y

;

u(x, y) =

+ xy + x -

+ 3y + C .

Тогда общий интеграл имеет вид

3x2 + 6xy + 6x - 2 y3 +18 y = C .

2 способ:

( x, y)

путь интегрирования

u(x, y) = ∫ (x + y + 1)dx + (x − y

3)dy = выберем

( x0 , y0 )

(x0 , y0 ) =

(0;0) → (x,0) → (x, y)

( x,0)

( x, y)

= ∫ (x + 0 + 1)dx + ∫ (x − y2 + 3)dy =

+ x + xy −

+ 3y.

(0,0)

( x,0)

Тогда общий интеграл имеет вид

+ x + xy -

+ 3y = C .

Такой же результат, как и в первом случае.

Пример 2. Решить уравнение e2 x - e x + y (1 + y¢) = 0 . Решение. Запишем исходное уравнение в виде

(e2 x - e x + y )dx - e x + y dy = 0

Так как для данного уравнения выполняется условие полного диф-

ференциала						∂P ;	∂Q
∂P = -e x+ y ;	∂Q = -e x+ y ,	т.е.	∂P =	∂Q и функции P,	Q,	∂P ;	∂Q
¶y	¶x		¶Y	¶x		¶y	¶x

непрерывны во всей плоскости, тогда общий интеграл уравнения имеет вид

2 x

x+ y

0+ y

2 x

x+ y

∫(e

- e

)dx + ∫ - e

dy = C

- e

= C .

или

Пример 3.

Найти интегральную кривую уравнения

(2xy -1)dx + (3y 2 + x2 )dy = 0 ,

проходящую через начало координат.

Решение.

Так

как

P(x,y)=2xy –

1, при

x =

0 и

y = 0

равна

P(0;0) = -1 ¹ 0 ,

то

формула (10)

∫(2xy -1)dx + ∫3y 2 dy = 0

или

x2 y - x + y3 = 0

дает искомое решение задачи Коши, а именно равенства

x2 y - x + y3 = 0

определяет

как функцию от

y, т.е.

x = x(y), удовлетво-

ряющую условию x(0) = 0

и искомому уравнению. Эта функция имеет вид

x = 1 - 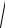1 - 4 y4 . 2 y

Интегрирующий множитель

Если уравнение (1) не является уравнением в полных дифференциа- лах, но удается найти такую функцию m = m(x, y) , что

		m × P(x, y)dx + m ×Q(x, y)dy = 0 .	(12)
и	¶(m × P) =	¶(m ×Q) .
	¶y	¶x
	Уравнение (12) – уравнение в полных дифференциалах,		тогда
m = m(x, y) –		интегрирующий множитель уравнения (1). Отметим, что если

уравнение (1) – уравнение в полных дифференциалах, то интегрирующий

множитель µ = 1.
	Если P(x,y)				и Q(x,y)	непрерывно дифференцируемы и
	P(x, y)	+	Q(x, y)	¹ 0	в области D,	то интегрирующий множитель сущест-

<<< < Предыдущая 1 2 3 45 / 225 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

Соседние файлы в папке Высшая математика (РТФ)

#
18.05.20153.63 Mб50умк_Вакульчик_Опред интеграл.pdf
#
18.05.20154.76 Mб34умк_Вакульчик_Элементы векторной алгебры.pdf
#
18.05.20155.38 Mб39умк_Вакульчик_Элементы линейной алгебры.pdf
#
18.05.20151.33 Mб42умк_Мальцев_Осн дискретной матем.pdf
#
18.05.20153.75 Mб40умк_Пальчик_Теория вероятностей.pdf
#
18.05.20155.68 Mб33умк_Цывис_Диф.уравнения_Ряды.pdf
#
18.05.20154.7 Mб40умк_Цывис_Функции_Интеграл. исчисл..pdf
#
18.05.20153.54 Mб77умк_Яско_ Диф.уравнения_Ряды.pdf