A third approach is based on the manipulations performed during longhand multiplication. For example, the multiplication of 00101101B (45 decimal) by 01101101B (109 decimal) can be expressed as a series of products and shifts, in the following manner:

The actual calculations in this method of binary multiplication are quite simple since the product by a 0 digit is zero and the product by a 1 digit is the multiplicand itself. Consequently, the multiplication routine simply tests each digit in the multiplier. If the digit is zero no action need be performed; if the digit is one, the multiplicand is shifted left and added into an accumulator.

The storage allocation to hold the product of a multiplication operation is not the same as that to hold the sum. In multi-byte addition one additional byte is required to hold the sum. In multiplication the storage allocation must be twice the size of the operands. For example, byte multiplication requires a two-byte storage, while multiplying two double-byte operands requires a four-byte storage allocation.

4.4.3 Unsigned Division

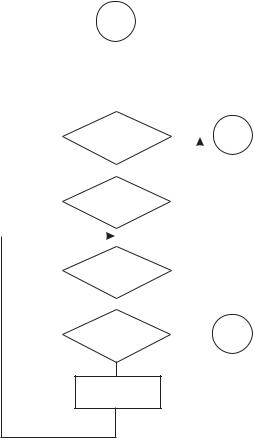
If multiplication can be reduced to repeated addition, then division can be conceptualized as repeated subtraction. In the case of division, the quotient (result) is the number of times the divisor must be subtracted from the dividend before zero or a negative value results from the subtraction. The flowchart in Figure 4-6 (in the following page) shows the logic steps in unsigned division.

In Figure 4-6 note that the logic tests for a zero divisor, since division by zero is mathematically undefined. Also, since the operation is unsigned, the result cannot be negative; therefore, the divisor must be larger than the dividend. Finally, the logic must consider the case in which subtracting the divisor from the reminder produces a negative value, in which case an adjustment is necessary to produce a valid quotient. This adjustment avoids the need for searching for a trial divisor, as in the case in the common longhand division algorithm. In machine code the negative result is detected as an overflow (carry flag set) from the subtraction.

4.5 Signed Binary Arithmetic

In two’s complement and sign-magnitude representations the high-order bit represents the sign of the operand, while its magnitude is represented in the remaining bits. Therefore, in the case of signed numbers, a carry out of the high-order bit is meaning-

These two examples show that the carry flag, by itself, cannot be used to detect an error or no-error condition in two’s complement arithmetic. Detecting an overflow condition in two’s complement representations requires observing the carry into the high-order bit of the encoding as well as the carry out. In both previous examples we note that there was a carry into the high-order bit of the result. However, in the first case there was no carry out. The general rule is: two’s complement overflow takes place when the carry into and the carry out of the high-order bit have opposite values. Figure 4-7 is a flowchart to detect overflow in signed arithmetic.

Figure 4-7 Detecting Overflow in Two’s Complement Arithmetic

Most microprocessors and some high-end microcontrollers contain hardware facilities for detecting signed arithmetic overflow. In some cases the hardware support consists of a single overflow flag that is set whenever the result of an arithmetic operation exceeds the capacity of the format. In other cases, as in the PIC 18CXX2 family, the status register contains a negative bit flag that indicates a 1-bit in the sign bit position, as well as an overflow bit that is set whenever there is an overflow from the magnitude bits (0 to 6) into the sign bit (bit 7) of the destination operand. In this device, software can test one or both of these flags to detect two’s complement overflow.

In lowand mid-range devices, with no hardware support for signed arithmetic, detecting a two’s complement overflow is by no means simple. Without a hardware flag to report a carry condition into a particular bit position, software is confronted with several possible alternatives, but none is simple or straightforward.

4.5.2 Sign Extension Operations

Observing the carry into and the carry out of the most significant bit is a valid way of detecting overflow of a two’s complement arithmetic operation. In theory, the logic described in the flowchart of Figure 4-7 can be implemented in devices without hard-