1.2. Решение текстовой задачи на симплексный метод линейного программирования.

Решим текстовую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.

Составим экономико-математическую модель.

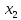Пусть – количество изделий первого типа необходимое для оптимального получения прибыли, тогда– количество изделий второго типа необходимое для оптимального получения прибыли,– количество изделий третьего типа,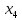– количество изделий четвертого типа.

Целевая функция, согласно прибыли от реализации изделий:

F(X) = 6x₁+2x₂+2,5x₃+4,5x₄, при следующих ограничениях, согласно заданной таблице норм затрат сырья на единицу типов изделий:

Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).

В 1-м неравенстве смысла (≤) вводим базисную переменную . В 2-м неравенстве смысла (≤) вводим базисную переменную. В 3-м неравенстве смысла (≤) вводим базисную переменную.

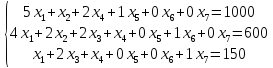
Решим систему уравнений относительно базисных переменных: x₅, x₆, x₇,

Полагая, что свободные переменные равны 0, получим первый опорный план: X1 = (0,0,0,0,1000,600,150), F(x)=0

Исходная симплексная таблица.

План 1.

Базис	переменные										Оцен. отношение
	x1	x2	x3	x4	x5	x6	x7
x5	5	1	0	2	1	0	0	1000		1000/5=200
x6	4	2	2	1	0	1	0	600		600/4=150
x7	1	0	2	1	0	0	1	150		150/1=150
	-6	-2	-2.5	-4.5	0	0	0	0

В строку записываем соответствующие числа с целевой функции, но с отрицательным знаком, так как целевая функция стремиться к максимуму. Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. В столбецзаписываем соответствующие запасы сырья.

Определим новую базисную переменную. В индексной строкевыбираем максимальный по модулю элемент. В качестве ведущего выберем столбец, соответствующий переменной x₁, так как это наибольший коэффициент по модулю.

Определим новую свободную переменную.

Вычислим значения оценочного отношения по строкам как частное от деления: b_i / a_i1 и из них выберем наименьшее: .

Следовательно, 2-ая строка является ведущей. Разрешающий элемент равен (4) и находится на пересечении ведущего столбца и ведущей строки. Поскольку в последнем столбце присутствует несколько минимальных элементов 150, то номер строки выбираем по правилу Креко.

Метод Креко заключается в следующем. Элементы строк, имеющие одинаковые наименьшие значения (min=150), делятся на предполагаемые разрешающие элементы, а результаты заносятся в дополнительные строки. За ведущую строку выбирается та, в которой раньше встретится наименьшее частное при чтении таблицы слева направо по столбцам, соответственно мы видим, что разрешающим элементом является 4.

Формируем следующую часть симплексной таблицы. Вместо переменной x₆ в План 2 войдет переменная x_1. Строка, соответствующая переменной x₁ в Плане 2, получена в результате деления всех элементов строки x₆ исходной таблицы на разрешающий элемент равный 4. На месте разрешающего элемента в плане 1 получаем 1.

В остальных клетках столбца x₁ плана 2 записываем нули, аналогично в столбцы х5 и х7 записываются элементы единичной матрицы, то есть

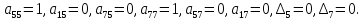
Все остальные элементы нового плана 2, включая элементы индексной строки, определяются по правилу прямоугольника. Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.

НЭ = (СТЭ*РЭ - А*В)/РЭ, СТЭ - элемент старого плана, РЭ - разрешающий элемент (4), А и В - элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ.

Представим расчет каждого элемента в таблицу:

=, ,

План 2.

Базис	переменные										Оцен. отношение
	x1	x2	x3	x4	x5	x6	x7
x5	0	-1,5	-2,5	0,75	1	-1,25	0	250		250/0,75=333,33
X1	1	0.5	-2,5	0.25	0	0.25	0	150		150/0,25=600
x7	0	-0,5	1,5	0,75	0	-0,25	1	0		0/0,75=0
	0	-0,5	0,5	-3	0	1,5	0	900

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.

X2 = (150, 0, 0, 0, 250, 0, 0), F(x) =900.

В индексной строке выбираем максимальный по модулю элемент. В качестве ведущего выберем столбец, соответствующий переменной x₄, так как это наибольший коэффициент по модулю.

Вычислим значения D_i ( оценочное отношение) по строкам как частное от деления: b_i / a_i4 и из них выберем наименьшее:

Следовательно, 3-ая строка является ведущей.

Разрешающий элемент равен (0.75) и находится на пересечении ведущего столбца и ведущей строки.

Формируем следующую часть симплексной таблицы. Вместо переменной x₇ в план 3 войдет переменная x₄ . Строка, соответствующая переменной x₄ в плане 3, получена в результате деления всех элементов строки x₇ плана 1 на разрешающий элемент РЭ=0.75

На месте разрешающего элемента в плане 2 получаем 1. В остальных клетках столбца x₄ плана 2 записываем нули, аналогично в столбцы х5 и х1 записываются элементы единичной матрицы. Все остальные элементы нового плана 3, включая элементы индексной строки, определяются по правилу прямоугольника.

Представим расчет каждого элемента в таблицу:

=, ,

План 3.

Базис	переменные										Оцен. отношение
	x1	x2	x3	x4	x5	x6	x7
x5	0	-1	-4	0	1	-1	-1	250		250/(-1)=
X1	1	0,67	0	0	0	0,33	-0,33	150		150/0,67=225
х4	0	-0,67	2	1	0	0,75	1,33	0		0/(-0,67)=
	0	-1	6,5	0	0	0,5	4	900

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.

X3 = (150, 0, 0, 0, 250, 0, 0), F(x)=900.

В индексной строке выбираем максимальный по модулю элемент. В качестве ведущего выберем столбец, соответствующий переменной x₂, так как это наибольший коэффициент по модулю.

Вычислим значения оценочного отношения по строкам как частное от деления: b_i / a_i2 и из них выберем наименьшее:

Следовательно, 2-ая строка является ведущей. Разрешающий элемент равен (0.67) и находится на пересечении ведущего столбца и ведущей строки.

Формируем следующую часть симплексной таблицы. Вместо переменной x₁ в план 4 войдет переменная x_2. Строка, соответствующая переменной x₂ в плане 4, получена в результате деления всех элементов строки x₁ плана 2 на разрешающий элемент РЭ=0.67. На месте разрешающего элемента в плане 4 получаем 1.

В остальных клетках столбца x₂ плана 4 записываем нули, аналогично в столбцы х5 и х4 записываются элементы единичной матрицы. Все остальные элементы нового плана 4, включая элементы индексной строки, определяются по правилу прямоугольника.

Представим расчет каждого элемента в таблицу:

=, ,

План 4.

Базис	переменные
	x1	x2	x3	x4	x5	x6	x7
x5	1,5	0	-4	0	1	-0,5	-1,5	475
X2	1,5	1	0	0	0	0,5	-0,5	225
х4	1	0	2	1	0	0	1	150
	1,5	0	6,5	0	0	1	3,5	1125

Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.

X4 = (0, 225, 0, 150, 475, 0, 0), F(x)=1125.

Итак, мы получили, что оптимальная месячная программа будет выполняться при 225 единиц количества изделий второго типа и 150 единиц количества изделий четвертого типа, причем мы видим, что выпускать изделия первого и третьего типа нецелесообразно, то есть сейчас фирма выпускает не оптимальный план продукции. Прибыль в этом случае составит 2*225 + 4.5*150 = 1125 усл.ед.

При нынешней месячной программе прибыль от реализации продукции составляет

10*6+200*2+10*2,5+120*4,5=1025 усл.ед., соответсвенно при выборе оптимальной программы дополнительный доход фирмы составит (1125-1025)=100 усл.ед.