Radiation Physics for Medical Physiscists - E.B. Podgorsak

After inserting Qα from (8.143) we get

M (P)c2 − M (D)c2 − mαc2

(EK)α = 1 + mα

MD

where AP is the atomic mass number of the parent nucleus; (AP − 4) is the atomic mass number of the daughter nucleus; and mα/M (D) ≈ 4/(AP − 4).

The kinetic energy (EK)D of the recoil daughter nucleus, on the other hand, is given as follows:

8.7.2 Alpha Decay of Radium-226 into Radon-222

For historical reasons, the most important example of radioactive decay in general and α decay in particular is the decay of radium-226 with a half-life of 1600 years into radon-222 which in itself is radioactive and decays by α decay into polonium-218 with a half-life of 3.824 days:

Radium-226 is the sixth member of the naturally occurring uranium series starting with uranium-238 and ending with stable lead-206. It was discovered in 1898 by Marie Curie and Pierre Curie and was used for therapeutic purposes almost immediately after its discovery, either as an external (sealed) source of radiation or as an internal (open) source.

The external use of radium-226 and radon-222 focused largely on treatment of malignant disease. In contrast, internal use of these two radionuclides was spread over the whole spectrum of human disease between 1905 through the 1930s and was based on ingestion of soluble radium salts, inhalation of radon gas or drinking water charged with radon.

When radium-226 is used as a sealed source, the radon-222 gas cannot escape and a build up occurs of the seven daughter products that form the radium-226 series. Some of these radionuclides undergo α decay, others β decay with or without emission of γ rays. The γ-ray spectrum consists of discrete lines ranging in energy from 0.18 MeV to 2.2 MeV producing a photon beam with an e ective energy close to that of cobalt-60 ( 1.25 MeV). The encapsulation of the source is thick enough to absorb all α and β particles emitted by radium-226 and its progeny; however, the encapsulation cannot stop the γ rays and this makes radium-226 sealed sources useful in treatment of cancer with radiation.

Before the advent of cobalt-60 and cesium-137 teletherapy machines in 1950s all external beam radiotherapy machines made use of radium-226.

320 8 Radioactivity

They were called teleradium machines, contained 4 to 10 g of radium-226 and were very expensive because of the tedious radium-226 manufacturing process. They were also very ine cient because of the low inherent specific activity of radium-226 (0.988 Ci/g = 3.665 × 1010 Bq/g) and self-absorption of γ radiation in the source.

•Widespread availability of external beam radiotherapy only started in the 1950s with the invention of the cobalt-60 teletherapy machine in Canada. On the other hand, radium-226 proved very practical for use in brachytherapy where sources are placed into body cavities or directly implanted into malignant lesions for a specific time.

•While radium-based brachytherapy was very popular in the past century, modern brachytherapy is now carried out with other radionuclides (e.g., iridium-192, cesium-137, iodine-125, etc.) that do not pose safety hazards associated with the radon-222 gas that may leak through damaged radium-226 source encapsulation.

The decay energy Qα for the α decay of radium-226 is calculated either using atomic rest masses M as given in (8.143) or nuclear rest masses M as given in (8.136) and (8.143) or nuclear binding energies EB as given in (8.137). All required data are given in Table 8.6 on page 353.

With appropriate atomic rest masses M and (8.143) we get

Qα = {M(22686Ra) − M(22286Rn) − M(42He)}c2 = 0.005232 × 931.5 MeV

while using appropriate binding energies EB and (8.137) we get the same result, as follows:

Qα = {EB(22286Rn) + EB(42He) − EB(22688Ra)}

= (1708.185 + 28.296 − 1731.610) MeV = 4.87 MeV . (8.151)

Using appropriate nuclear rest energies M c2 in conjunction with (8.13) or (8.143) we also obtain Qα = 4.87 MeV.

The kinetic energy (EK)α of the α particle is given from (8.147) as

while 0.09 MeV goes into the recoil kinetic energy (EK)D of the 22286Rn atom, as calculated from (8.148)

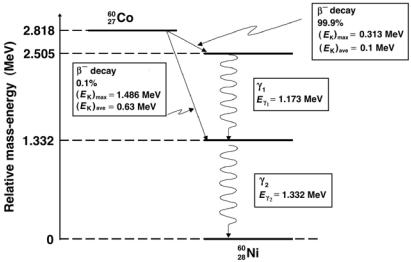
Figure 8.19 shows an energy level diagram for radium-226 decaying through α decay into radon-222. A closer look at the decay scheme of 22688 Ra, shown in Fig. 8.19, paints a slightly more complicated picture with two α lines

Fig. 8.19. Energy level diagram for the α decay of radium-226 into radon-222. The relative mass-energy levels for the ground states of the two nuclides are calculated from the respective atomic masses of the two radionuclides given in Table 8.6 on page 353

emitted; one with (EK)α1 = 4.78 MeV emitted in 94.6% of decays and the other with (EK)α2 = 4.60 MeV emitted in 5.4% of the decays. The 4.78 MeV transition ends at the ground state of 22286Rn; the 4.60 MeV transition ends at the first excited state of 22286Rn that instantaneously decays to the ground state through emission of a 0.18 MeV gamma ray (gamma decay; see Sect. 8.12).

The decay energy Qα of 4.87 MeV is thus shared between the α particle (4.78 MeV) and the recoil daughter (0.09 MeV). The α particle, because of its relatively small mass in comparison with the daughter mass, picks up most of the decay energy; the magnitudes of the momenta for the two decay products are of course equal, but the momenta are opposite in direction to one another.

8.8 Beta Decay

8.8.1 General Aspects of Beta Decay

The term β decay encompasses modes of radioactive decay in which the atomic number Z of the parent nuclide changes by one unit (±1), while the atomic mass number A remains constant. Thus, the number of nucleons and the total charge are both conserved in the β decay processes and the daughter (D) can be referred to as an isobar of the parent (P).

Three processes fall into the category of β decay:

1. β− decay with the following characteristics: Z → Z + 1; A = const

322 8 Radioactivity

A neutron-rich radioactive nucleus transforms a neutron into proton and ejects an electron and an antineutrino. Free neutrons actually decay into protons through the β− decay process with a life-time τ of 10.24 min. This decay is possible since the neutron rest mass exceeds that of the proton.

2. β+ decay with the following characteristics: Z → Z − 1; A = const:

A proton-rich radioactive nucleus transforms a proton into neutron and ejects a positron and a neutrino. Free protons cannot decay into neutrons through a β+ decay process because the rest mass of the proton is smaller than that of the neutron.

3. Electron capture with the following characteristics: Z → Z −1; A = const:

A proton-rich radioactive nucleus captures an inner shell orbital electron (usually K shell), transforms a proton into a neutron, and ejects a neutrino.

In many cases, β decay of a parent nucleus does not lead directly to the ground state of the daughter nucleus; rather it leads to an unstable or even metastable excited state of the daughter. The excited state de-excites through emission of gamma rays or through emission of internal conversion electrons (see Sect. 8.12). Of course, the orbital shell vacancies produced by the electron capture or internal conversion process will be followed by emission of discrete characteristic photons or Auger electrons, as is the case with all shell vacancies no matter how they are produced. A detailed discussion is given in Chap. 3. Beta decay can only take place when the binding energy of the daughter nucleus Eb(D) exceeds the binding energy of the parent nucleus EB(P).

8.8.2 Beta Particle Spectrum

For a given β decay, similarly to the situation in α decay, the β-decay energy is uniquely defined by the di erence in mass-energy between the parent and daughter nuclei. However, in contrast to the α decay where the energy of the emitted α particles is also uniquely defined, the β particles emitted in β decay are not mono-energetic, rather they exhibit a continuous spectral kinetic energy distribution with only the maximum kinetic energy (Ee± )max corresponding to the β decay energy.

This apparent contravention of the energy conservation law was puzzling physicists for many years until in 1930 Wolfgang Pauli postulated the existence of the neutrino to explain the continuous spectrum of electrons emitted in β decay. In 1934 Enrico Fermi expanded on Pauli’s neutrino idea and developed a theory of the β− and β+ decay. Only with the emission of a third

Fig. 8.20. Typical beta particle energy spectra for β− and β+ decay normalized to the maximum energy of the β particle

particle, the neutrino or antineutrino, could the momentum and energy be conserved in a β decay. The existence of the neutrino was finally proven experimentally in 1953.

The neutrino and antineutrino are assumed to have essentially zero rest mass and are moving with the speed of light c. They are also assumed to have only weak interactions with atoms of the absorber and are thus extremely di cult to detect. Their charge is equal to zero. It is obvious that detection of an essentially massless, momentless, uncharged relativistic particle that only experiences weak interactions with matter is extremely di cult. Nonetheless, several techniques were devised to detect the elusive particle experimentally and thus prove correct Fermi’s contention about its existence in beta decay.

Typical shapes of β− and β+ spectra are shown in Fig. 8.20. In general, the spectra exhibit low values at small kinetic energies, reach a maximum at a certain kinetic energy and then decrease with kinetic energy until they reach zero at a maximum energy (Ee± )max that corresponds to the β decay energy Qβ , if we neglect the small recoil energy acquired by the daughter nucleus.

The shapes of β− and β+ spectra di er at low kinetic energies owing to the charge of the β particles: electrons in β− decay are attracted to the nucleus; positrons in β+ decay are repelled by the nucleus. The charge e ects cause an energy shift to lower energies for electrons and to higher energies for positrons, as is clearly shown in Fig. 8.20.

For use in internal dosimetry calculations of β sources the e ective energy (Ee± )e of β decay spectra is usually estimated as

324 8 Radioactivity

8.8.3 Daughter Recoil in β− and β+ Decay

In a β− and β+ beta decay event the daughter nucleus recoils with a kinetic energy (EK)D ranging from 0 to a maximum value.

1.The recoil kinetic energy of the daughter decay product is zero, i.e., (EK)D = 0 when the electron and antineutrino in β− decay or positron and neutrino in β+ decay are emitted with the same momentum but in opposite directions.

2.The maximum recoil kinetic energy (EK)Dmax = max of the daughter occurs when either one of the two decay particles (electron or antineutrino in β− decay; positron or neutrino in β+ decay) is emitted with the maximum available kinetic energy (Eβ )max. The β decay energy Qβ is expressed as

The maximum recoil kinetic energy of the daughter (EK)D is determined using the laws of energy and momentum conservation and accounting for the relativistic mass changes of the β particle (electron or positron). A common name for electron or positron in beta decay is β particle.

1.The β particle momentum pe± = γme± υe± is equal to the daughter momentum pD = M (D)υD, where me± and M (D) are the rest masses of the β particle and daughter nucleus, respectively; υe± and υD are the velocities of the β particle and the daughter nucleus, respectively; and γ = (1 − β2)−1/2 with β = υ/c.

2.The kinetic energy (EK)D of the daughter nucleus is calculated classically

as (EK)D = M (D)υD2 /2; the maximum kinetic energy of the β particle is given relativistically as (Eβ )max = (γ − 1)me± c2.

Inserting (8.159) into the equation for the daughter kinetic energy (EK)D = M (D)υD2 /2, we obtain

Inserting (8.161) into (8.160) we obtain the following expression for the recoil kinetic energy (EK)D of the daughter nucleus:

The daughter recoil kinetic energy (EK)D is usually of the order of 10 eV to 100 eV; negligible in comparison to the kinetic energy of the β particle, yet su ciently high to be able to cause atomic rearrangements in the neighboring molecules in biological materials.

The decay energy Qβ is now given as follows:

showing that in β− and β+ decay by far the larger energy component is the component shared between the β particle and neutrino, since these two particles in general share the energy (Eβ )max; the recoil kinetic energy given to the daughter is extremely small and may be neglected, unless, of course, we are interested in calculating it, so that we may determine the local damage produced by the daughter atom in biological materials.

8.9 Beta Minus Decay

8.9.1 General Aspects of Beta Minus (β−) Decay

Several radionuclides decaying by β− decay are used in medicine for external beam radiotherapy and brachytherapy. The parent nuclide decays by β− decay into an excited daughter nuclide that instantaneously or through a metastable decay process decays into its ground state and emits the excitation energy in the form of gamma ray photons. These photons are then used for radiotherapy.

The most important characteristics of radionuclides used in external beam radiotherapy are:

1.High gamma ray energy

2.High specific activity

3.Relatively long half-life

4.Large specific air-kerma rate constant

Of the over 3000 natural or artificial radionuclides known, only a few are suitable for use in radiotherapy and of these practically only cobalt-60, with its high photon energy (1.17 MeV and 1.33 MeV), high practical specific activity, and a relatively long half-life (5.27 years), meets the source requirements for external beam radiotherapy.

326 8 Radioactivity

8.9.2 Beta Minus (β−) Decay Energy

The β− decay can occur to a neutron-rich unstable parent nucleus when the mass M (Z, A) of the parent nucleus exceeds the mass M (Z + 1, A) of the daughter nucleus by more than one electron rest mass me. The decay energy Qβ− for the β− decay process is given as

in terms of nuclear mass M .

Adding and subtracting Zmec2 to the right-hand side of (8.164) and neglecting the electron binding energies to the nucleus we obtain

where M(Z, A) and M(Z + 1, A) represent the atomic masses of the parent and daughter, respectively, noting that

For the β− decay to occur the atomic mass of the parent M(Z, A) must exceed the atomic mass of the daughter M(Z + 1, A); i.e., M(Z, A) > M(Z + 1, A).

The atomic rest energy di erence between the parent and daughter provides the energy released in a β− decay event, most generally consisting of:

1.Energy of the emitted electron

2.Energy of the antineutrino

3.Energy of the emitted γ ray photons or conversion electrons with characteristic x rays and Auger electrons.

4.Recoil kinetic energy of the daughter nucleus (small and usually neglected).

8.9.3 Beta Minus (β−) Decay of Cobalt-60 into Nickel-60

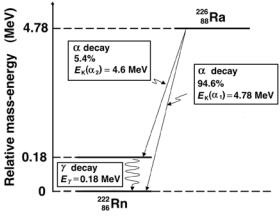
For medical physics an important β− decay example is the decay of unstable cobalt-60 radionuclide with a half life of 5.27 years into an excited nickel-60 nuclide that decays instantaneously into its ground state with emission of two γ ray photons of energies 1.173 MeV and 1.332 MeV, as shown schematically in Fig. 8.21:

Cobalt-60 is used as a radiation source in teletherapy machines applied for external beam radiotherapy. Typical cobalt-60 source activities are of the order of 200 TBq to 400 TBq. There are several thousand cobalt units in