
Zadachai_OTN
.pdf
Формулы для нормального закона распределения времени безотказной работы изделия примут вид
p(t) 0,5 Ф(U);U |
t mt |
; |
|
|
|
(1.35) |
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
q(t) 0,5 Ф(U);Ф(U) |
1 |
|
|
|
|
u |
|
U2 |
(1.36) |
||||||||||||
|
|
|
e |
2 |
|
dU; |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
|
|
|
|||||
|
Ф(U) |
|
|
1 |
|
|
|
|
U2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
f (t) |
|
|
;Ф(U) |
|
|
e |
2 |
|
; |
(1.37) |
|||||||||||
|
|
2 |
|
||||||||||||||||||
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(t) |
Ф(U) |
|
|
|
1 |
|
|
|
, |
|
|
|
(1.38) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
t |
0,5 Ф(U) |
|
|
|
|||||||||||||||
где Ф(U) – функция Лапласа, обладающая свойствами: |
|
|
|
||||||||||||||||||
Ф(0)=0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.39) |
Ф(-U) =-Ф(U) ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.40) |
mt – среднее значение случайной величины Т; |
|
|
|
|
|
|
|
|
|
|
|||||||||||
t2 – дисперсия случайной величины Т;
Т – время безотказной работы изделия.
Формулы для закона распределения Вейбулла времени безотказной работы изделия имеют вид:
p(t) e at2 |
; |
|
(1.41) |
q(t ) 1 e at2 |
; |
(1.42) |
|
f (t) aktk 1 |
p(t); |
(1.43) |
|
(t) aktk 1; |
|
|
(1.44) |
23
|
|
1 |
Г( |
1 |
) |
|
|
||
|
|
k |
|
|
|
||||
m(t) |
|
|
|
|
к |
; |
(1.45) |
||
|
|
|
1 |
|
|
||||
|
|
|
|
|
|
|
|||
ak
где a, k - параметры закона распределения Вейбулла.
Формулы для закона распределения Релея времени безотказной работы изделия имеют следующий вид:
p(t) exp( |
t2 |
); |
|
|
|
||||
2 t2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
||
q(t) 1 exp( |
t2 |
|
); |
|
|||||
2 t2 |
|
|
|||||||
|
|
|
|
|
|
|
|||
f (t) |
t |
exp( |
|
t |
2 |
); |
|||
t2 |
|
2 t2 |
|||||||
|
|
|
|
|
|
||||
(t) |
t |
|
; |
|
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
||
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m(t) t |
|
|
|
|
; |
||
|
|
|
|||||
2 |
|||||||
где t – мода распределения случайной величины Т;
Т– время безотказной работы изделия.
Задача 1.4
(1.46)
(1.47)
(1.48)
(1.49)
(1.50)
Прочность объекта и нагрузка описываются случайными процессами, которые в сечениях подчиняются закону Релея. Необходимо рассчитать и построить функцию надежности, ненадежности, плотности распределения наработки до отказа, интенсивности отказов. Процесс, описывающий прочность – нестационарный. Нагрузка – стационарна. Дана функция усталости:
t exp k t и математические ожидания прочности: п t 0 (при t=0) и
нагрузки н. Диапазон наработки выбрать самостоятельно в пределах 100– 150 часов.
Исходные данные к задаче 1.4. приведены в таблице 1.8.
24
Таблица 1.8 – Исходные данные
Вари- |
k, |
1 |
|
t 0 ,Н |
|
,Н |
Вари- |
k, |
1 |
|
t 0 ,Н |
|
,Н |
|
ант |
ант |
|||||||||||||
|
|
п |
|
н |
|
|
п |
|
н |
|||||
ч |
|
|
|
|
|
ч |
|
|
|
|
|
|||
1, 31 |
0,01 |
|
10 |
|
4 |
15, 46 |
0,01 |
|
12 |
|
5 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
2, 32 |
0,012 |
|
12 |
|
5 |
16, 47 |
0,012 |
|
14 |
|
4 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
3, 33 |
0,014 |
|
14 |
|
6 |
17, 48 |
0,014 |
|
16 |
|
7 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
4, 34 |
0,016 |
|
16 |
|
7 |
18, 49 |
0,016 |
|
18 |
|
6 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
5, 35 |
0,018 |
|
18 |
|
8 |
19, 50 |
0,018 |
|
20 |
|
7 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
6, 36 |
0,02 |
|
20 |
|
4 |
20, 51 |
0,02 |
|
22 |
|
8 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
7, 37 |
0,01 |
|
22 |
|
5 |
21, 52 |
0,01 |
|
14 |
|
4 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
8, 38 |
0,012 |
|
10 |
|
6 |
22, 53 |
0,012 |
|
10 |
|
5 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
9, 39 |
0,014 |
|
12 |
|
7 |
23, 54 |
0,014 |
|
12 |
|
6 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
10, 40 |
0,016 |
|
14 |
|
8 |
24, 55 |
0,016 |
|
14 |
|
7 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
11, 41 |
0,018 |
|
16 |
|
4 |
25, 56 |
0,018 |
|
16 |
|
8 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
12, 42 |
0,02 |
|
18 |
|
5 |
26, 57 |
0,02 |
|
18 |
|
4 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
13, 43 |
0,011 |
|
20 |
|
6 |
27, 58 |
0,011 |
|
20 |
|
5 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
14, 44 |
0,013 |
|
22 |
|
7 |
28, 59 |
0,015 |
|
22 |
|
6 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
29, 45 |
0,012 |
|
21 |
|
5 |
30, 60 |
0,016 |
|
24 |
|
7 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для вариантов 31-60 к исходным данным математического ожидания надо прибавить цифру 1.
1.4 Модель отказов с марковской аппроксимацией параметра
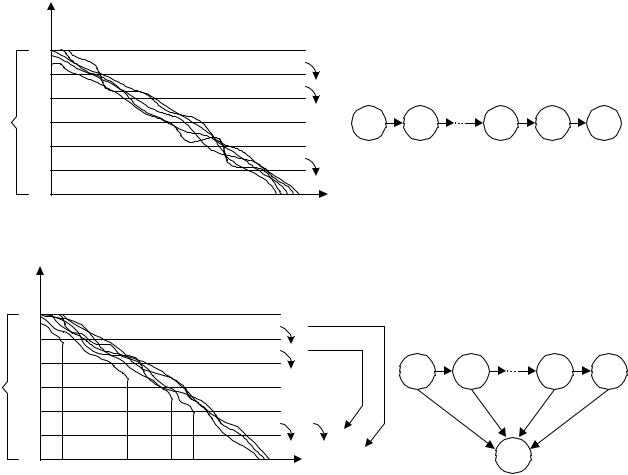
Рассмотрим случайный процесс с непрерывным пространством состояний – процесс изменения параметра объекта (рис. 1.3). Диапазон допустимого по техническим условиям изменения параметра разделим на n квантов (интервалов). Такая процедура называется квантованием по уровню. Считаем, что объект находится в состоянии i, если значение параметра х(t) лежит в i-м интервале квантования. В зависимости от характера возникающих отказов объект может либо последовательно проходить через всю цепь работоспособных состояний 0, 1, 2, … i, … n – 1 и достигать состояния отказа n (постепенный отказ) (рис. 1.3, а), либо за один переход, мгновенно попадать из любого состояния i 1 … n – 1 в состояние отказа (внезапный отказ) (рис. 1.3, в).
25
x(t) |
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
1 |
1 |
|
0 |
|
|
i |
|
|
. |
|
0 |
1 |
i |
n-1 |
n |
||
i |
|
|
1 |
|
n-1 |
|||
n-1 |
|
|
|
|
|
|
|
|
n-1 |
|
|
б) граф состояний и |
|
||||
n |
|
|
|
|
||||
|
t |
|
|
переходов для «а)» |
|
|||
|
а) постепенные отказы |
|
|
|
|
|
|
|
x(t) |
|
|
|
|
|
|
|
0 |
0 |
|
0 |
1 |
|
|
i |
1 |
1 |
0 |
|
i |
|||
. |
|
|
1 |
|
n-1 |
||
i |
|
1 |
|
1 |
|
i |
|
n-1 |
n-1 |
0 |
0 |
|
n-1 |
||
|
|
|
|||||
n |
t |
n-1 |
|
|
n |
n-1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
в) постепенные и внезапные отказа |
г) граф состояний и |
|
переходов для «в)» |
Рис. 1.3 – Графы состояний при постепенных и внезапных отказах
Задача 1.5
Модель отказов трубчатого разрядника предполагает наличие внезапных отказов и отказов из-за износа фибры. Известны интенсивности
внезапных отказов из исправного состояния 0 1/год; из состояния пре-
дотказов 1 1/год; интенсивность износа 0 1/год и интенсивность посте-
пенных отказов из состояния предотказов 1 1/год.
Найти зависимость функции надежности, плотности распределения наработки до отказа и интенсивности отказов от наработки. Рассчитать математическое ожидание наработки до отказа. Построить графики функций.
Исходные данные приведены в таблице 1.9.
26
Таблица 1.9 – Исходные данные к задаче 1.5.
Вариант |
0 |
0 |
1 |
1 |
1 |
0,05 |
0,02 |
0,06 |
0,04 |
2 |
0,04 |
0,02 |
0,05 |
0,03 |
3 |
0,07 |
0,02 |
0,05 |
0,02 |
4 |
0,03 |
0,02 |
0,06 |
0,03 |
5 |
0,09 |
0,04 |
0,1 |
0,05 |
6 |
0,05 |
0,03 |
0,08 |
0,04 |
7 |
0,06 |
0,05 |
0,08 |
0,06 |
8 |
0,06 |
0,02 |
0,07 |
0,04 |
9 |
0,04 |
0,01 |
0,06 |
0,04 |
10 |
0,06 |
0,04 |
0,08 |
0,05 |
11 |
0,04 |
0,02 |
0,06 |
0,03 |
12 |
0,09 |
0,03 |
0,1 |
0,04 |
13 |
0,08 |
0,02 |
0,09 |
0,04 |
14 |
0,06 |
0,04 |
0,09 |
0,06 |
15 |
0,08 |
0,05 |
0,1 |
0,07 |
16 |
0,02 |
0,01 |
0,06 |
0,03 |
17 |
0,03 |
0,01 |
0,07 |
0,05 |
18 |
0,04 |
0,02 |
0,06 |
0,04 |
19 |
0,05 |
0,03 |
0,06 |
0,04 |
20 |
0,03 |
0,02 |
0,08 |
0,05 |
21 |
0,03 |
0,03 |
0,05 |
0,04 |
22 |
0,03 |
0,03 |
0,05 |
0,02 |
23 |
0,04 |
0,02 |
0,06 |
0,02 |
24 |
0,04 |
0,01 |
0,07 |
0,05 |
25 |
0,05 |
0,03 |
0,07 |
0,06 |
26 |
0,05 |
0,02 |
0,06 |
0,03 |
27 |
0,06 |
0,05 |
0,08 |
0,06 |
28 |
0,07 |
0,06 |
0,1 |
0,03 |
Решение:
Перечислим все возможные состояния объекта и перенумеруем их:
0– исправное состояние;
1– состояние предотказа;
2– состояние отказа;
Изобразим и разметим граф состояний и переходов модели марковской аппроксимации (рис. 1.4).
0
0  1
1
0 |
1 |
+ 1 |
|
2 |
|
Рисунок 1.4 – Граф состояний для модели
27
Можно составить уравнения Колмогорова для каждого состояния
|
dP0(t ) |
|
( )P (t ) |
|
|
|
||||||
dt |
|
|
|
|||||||||
|
|
|
0 |
0 |
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||
dP(t ) |
0P0(t ) |
( 1 |
|
|
)P1(t ) |
(1.51) |
||||||
|
1 |
|
|
|
1 |
|||||||
dt |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
dP2(t ) |
P (t ) ( |
1 |
)P(t ) |
|
|||||||
|
|
|||||||||||
|
dt |
|
|
0 0 |
|
1 |
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|||
Решать систему уравнений можно различными способами. Воспользовавшись операционными методом получили
P(t) A |
e( Kit) |
(1.52) |
|
i |
in |
|
|
В данном случае коэффициенты
|
|
|
A02 |
1 |
|
|
0 |
(1.53) |
|
|
|
|
K1 K0 |
||||||
|
|
|
|
|
|
|
|||
|
|
|
A |
|
|
|
0 |
, |
(1.54) |
|
|
|
|
|
|
||||
|
|
|
12 |
|
K1 |
K0 |
|
||
|
|
|
|
|
|
||||
где |
K0 = 0 |
0 |
1/год; |
|
|
|
|
|
|
|
K1 1 |
1 |
1/год. |
|
|
|
|
|
|
Функция надежности:
F t P0 t P1 t A02 exp K0t A12 exp K1t . |
(1.56) |
Плотность распределения наработки до отказа:
q t K0 A02 exp K0t K1A12 |
exp K1t . |
(1.55) |
||||
Интенсивность отказов: |
|
|
|
|
|
|
(t) |
K0 A02 |
exp( K |
0t) K1A12 exp( K0t) |
. |
(1.56) |
|
A02 |
exp( K |
|
||||
|
0t) A12 |
exp( K1t) |
|
|||
Математическое ожидание наработки до отказа:
T |
|
A02 |
|
A12 |
год. |
(1.57) |
K0 |
|
|||||
|
|
|
K1 |
|
||
28
|
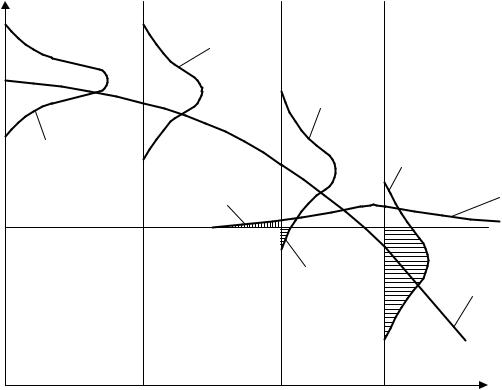
1.5 Модель отказа – параметр поля допуска |
|
||
При эксплуатации объектов часто имеется возможность контроля па- |
||||
раметров и их работоспособности. Поэтому возникает необходимость уста- |
||||
новления аналитической связи характеристик, описывающих изменение па- |
||||
раметров элементов, с показателями надежности. Такую связь помогает |
||||
установить модель отказа параметр – поле допуска, представленная на |
||||
рис 1.5. Случайный процесс изменения параметра представлен сечениями, в |
||||
которых располагаются кривые плотности распределения параметра в опре- |
||||
деленные моменты времени f(x, t). Различают модели с одно - и двухсторон- |
||||
ним полем допуска. Границы поля допуска могут задаваться как неслучайной |
||||
величиной xдоп, так и случайными величинами f (xдоп), а также случайными |
||||
процессами f (t, xдоп) (стационарными и нестационарными). Наибольший ин- |
||||
терес для практики представляет случай, когда изменение параметра описы- |
||||
вается нестационарным случайным процессом, а граница поля допуска явля- |
||||
ется неслучайной величиной (рис. 1.5). В этом случае граница поля допуска – |
||||
предельная величина параметра, при которой объект становится неработо- |
||||
способным. |
|
|
|
|
x(t) |
Модель отказа параметр - поле допуска |
|
||
|
|
|
|
|
|
|
f(x, t1) |
|
|
|
|
f(x, t2) |
|
|
|
f(x, 0) |
|
f(x, t3) |
|
|
|
Q(t2) |
|
q(t) |
xдоп |
|
|
|
|
|
|
Q(xдоп, t2) |
|
(t) |
0 |
t1 |
t2 |
t3 |
t |
|
Рис. 1.5 Модель отказа параметр – поля допуска |
|
||
29
Допущения:
закон распределения параметра f(x, t) во времени не изменяется;
реализации xi(t) и моментные функции параметров плотности распределения f(x, t) во времени изменяются монотонно;
в начальный момент времени значения параметров находятся в границах поля допуска.
Плотность вероятности того, что за время dt, включающее момент t, значение параметра выйдет за границы поля допуска, составляет:
Моментные функции параметров распределения f(x, t) аппроксимируются следующими зависимостями:
t a b t , |
(1.58) |
t a exp b t , |
(1.59) |
t a tb, |
(1.60) |
t a exp b t c , |
(1.61) |
t a tb c, |
(1.62) |
Задача 1.6
Модель отказа: параметр–поле допуска. Закон распределения реализаций в сечениях процесса – закон Релея. Даны: моментная функция параметра распределения Релея t a b t и граница поля допуска xдоп. В начальный момент времени значение параметра, характеризующего состояние объекта, находится в границах поля допуска и равно нулю. Построить графические зависимости плотности наработки до отказа, функции надежности, функции ненадежности, интенсивности отказов за наработку от 0 до 500 ч.
Исходные данные приведены в таблице 1.10.
Таблица 1.10. – Исходные данные
Вариант |
a |
b, мес-1 |
xдоп, Н |
Вариант |
a |
b |
xдоп |
1, 29 |
10 |
0,1 |
40 |
15,43 |
15 |
0,1 |
44 |
2, 30 |
11 |
0,11 |
42 |
16,44 |
16 |
0,11 |
46 |
3,31 |
12 |
0,12 |
44 |
17,45 |
17 |
0,12 |
48 |
4, 32 |
13 |
0,13 |
46 |
18,46 |
18 |
0,13 |
50 |
5, 33 |
14 |
0,14 |
48 |
19,47 |
10 |
0,14 |
40 |
6,34 |
15 |
0,15 |
50 |
20,48 |
11 |
0,15 |
42 |
7,35 |
16 |
0,16 |
40 |
21,49 |
12 |
0,16 |
44 |
8,36 |
17 |
0,1 |
42 |
22,50 |
13 |
0,1 |
46 |
9,37 |
18 |
0,11 |
44 |
23,51 |
14 |
0,11 |
48 |
10,38 |
10 |
0,12 |
46 |
24,52 |
15 |
0,12 |
50 |
11,39 |
11 |
0,13 |
48 |
25,53 |
16 |
0,13 |
40 |
30
Продолжение таблицы 1.10
12,40 |
12 |
0,14 |
50 |
26,54 |
17 |
0,14 |
42 |
13,41 |
13 |
0,15 |
40 |
27,55 |
18 |
0,15 |
44 |
14,42 |
14 |
0,16 |
42 |
28,56 |
10 |
0,16 |
46 |
Для Вариантов 29 – 56 к значению a приплюсовать цифру 1.
1.6 Восстанавливаемые объекты
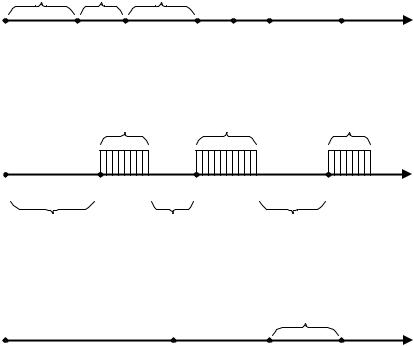
Рассмотрим процесс эксплуатации восстанавливаемого объекта (рис. 1.6, б). В момент времени, равный нулю, новый работоспособный объект был включен в работу. В течение некоторого промежутка времени (0, t1) равного t01 объект работал и в момент времени t1 отказал. Мгновенно за наступлением отказа начинается восстановление. Восстановление продолжается в течение времени tв1, затем объект опять включается в работу и работает до наступления следующего отказа. Обычно принимают допущения о том, что все восстановления полные, тогда процесс эксплуатации такого объекта может продолжаться бесконечно долго. Большинство устройств системы электроснабжения – трансформаторы, выключатели, преобразователи, контактная подвеска и др. являются восстанавливаемыми объектами. Однако далеко не всегда к ним может применяться допущение о полном восстановлении, но на небольших промежутках времени такое допущение вполне справедливо. Как можно видеть из рис. 6, б события – последовательные наступления отказов и окончания восстановлений разделены случайным промежутком времени. Допустим, что время наработки между отказами и время восстановления являются независимыми случайными величинами. Законы распределения времени могут быть различными. Показатели надежности восстанавливаемых объектов рассчитываются на основе учета наработки между отказами и временем восстановления. Поэтому расчет показателей надежности восстанавливаемых объектов в общем сложнее, чем для невосстанавливаемых. Некоторые объекты имеют время наработки между отказами значительно больше времени восстановления. Например, анкерный участок контактной сети между отказами работает годы, а время восстановления после обрыва проводов составляет в среднем 1,5 – 3 ч. Отказавший объект может также быстро заменяться на исправный и ремонтироваться вне процесса применения. Для таких объектов, при расчете показателей надежности время восстановления можно принять равным нулю. Следовательно, можно выделить два класса восстанавливаемых объектов: с нулевым (рис. 6, а) и с конечным (рис. 6, б) временем восстановления.
31
t01 |
|
t02 |
t03 |
|
|
0 |
t1 |
t2 |
t3 t4 t5 |
t6 |
t |
а) объект с нулевым временем восстановления |
|
||||
|
|
tв1 |
tв2 |
tв3 |
|
0 |
|
t1 |
t2 |
t3 |
t |
t01 |
|
|
t02 |
t03 |
|
б) объекты с конечным временем восстановления
Δt
0 |
τ |
t |
t+Δt |
t |
в) промежуток времени
Рис. 1.6 – События потока отказов восстанавливаемых объектов
Параметры распределения наработки между отказами могут быть найдены с использованием тех же параметрических или непараметрических моделей, что и для невосстанавливаемых объектов (см. предыдущий раздел). Случайная величина времени восстановления определяется многими факторами (время обнаружения при отсутствии мгновенной индикации отказа, время доставки бригады, время работы, зависящее от методов организации восстановления и т. д.).
1.7 Оценка показателей надежности восстанавливаемого объекта
Задача 1.7
Имеются данные эксперимента – наблюдения за отказами и восстановлениями одного восстанавливаемого объекта (Таблица 1.11).
Требуется найти оценки:
–математического ожидания наработки на отказ;
–математического ожидания времени восстановления;
–математического ожидания между событиями потока;
–коэффициента готовности;
–функциональной зависимости параметра потока отказов от наработки с интервалом в 1000 ч.
32
