1. Вариант 1

2. 1. Применяя необходимое и достаточное условия экстремума функции двух переменных, найти стационарные точки и экстремумы функции

3. 2. Найти экстремумы функции двух переменных , если переменные связаны условием

4. 3. Найти наибольшее и наименьшее значение функции z=z(x,y), заданной неявно соотношением x+2y+3z‑14=0 в области, ограниченной линиями 1, , , .

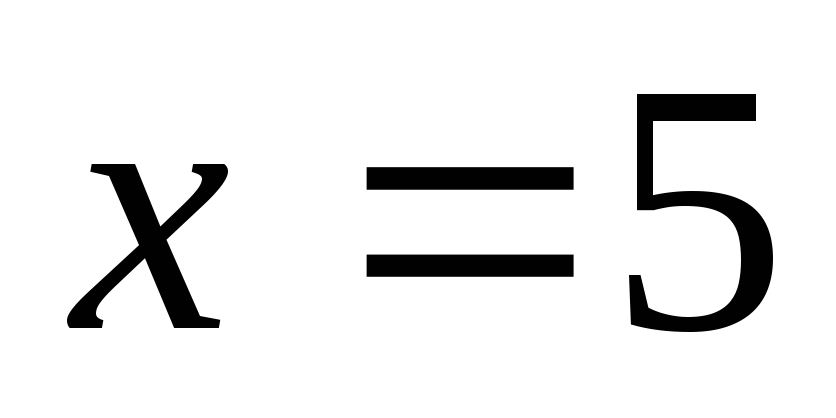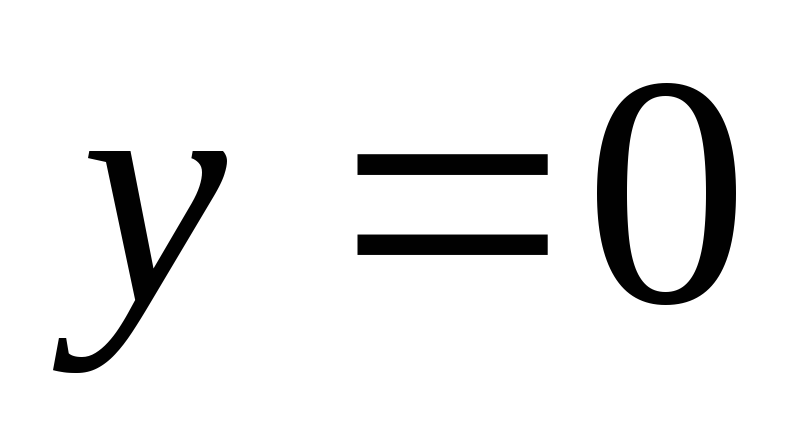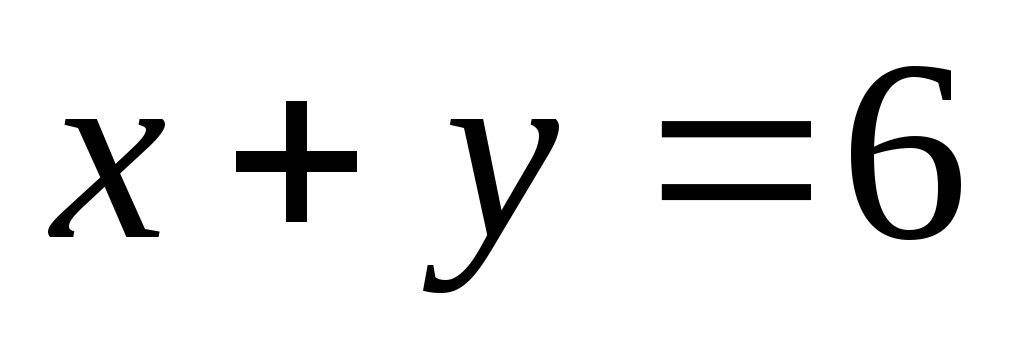4. С помощью метода Лагранжа найти условные экстремумы функции z=z(x,y) при указанной связи между аргументами. Изобразить ответ и связь между аргументами на плоскости Оху. ,

Вариант 2

1. Применяя необходимое и достаточное условия экстремума функции двух переменных, найти стационарные точки и экстремумы функции

2. Найти экстремумы функции двух переменных , если переменные связаны условием

3. Найти наибольшее и наименьшее значение функции z=z(x,y), заданной неявно соотношением x+2y‑5z+20=0 в области, ограниченной линиями , , , .

4. С помощью метода Лагранжа найти условные экстремумы функции z=z(x,y) при указанной связи между аргументами. Изобразить ответ и связь между аргументами на плоскости Оху. ,

Вариант 3

1. Применяя необходимое и достаточное условия экстремума функции двух переменных, найти стационарные точки и экстремумы функции

2. Найти экстремумы функции двух переменных , если переменные связаны условием

3. Найти наибольшее и наименьшее значение функции z=z(x,y), заданной неявно соотношением x‑3y+7z‑24=0 в области, ограниченной линиями , , , .

4. С помощью метода Лагранжа найти условные экстремумы функции z=z(x,y) при указанной связи между аргументами. Изобразить ответ и связь между аргументами на плоскости Оху. ,

Вариант 4

1. Применяя необходимое и достаточное условия экстремума функции двух переменных, найти стационарные точки и экстремумы функции

2. Найти экстремумы функции двух переменных , если переменные связаны условием

3. Найти наибольшее и наименьшее значение функции z=z(x,y), заданной неявно соотношением 2x‑y+4z=0 в области, ограниченной линиями , , , .

4. С помощью метода Лагранжа найти условные экстремумы функции z=z(x,y) при указанной связи между аргументами. Изобразить ответ и связь между аргументами на плоскости Оху. ,

Вариант 5

1. Применяя необходимое и достаточное условия экстремума функции двух переменных, найти стационарные точки и экстремумы функции

2. Найти экстремумы функции двух переменных , если переменные связаны условием

3. Найти наибольшее и наименьшее значение функции z=z(x,y), заданной неявно соотношением 3x+y‑5z‑12=0 в области, ограниченной линиями , , , .

4. С помощью метода Лагранжа найти условные экстремумы функции z=z(x,y) при указанной связи между аргументами. Изобразить ответ и связь между аргументами на плоскости Оху. ,

Вариант 6

1. Применяя необходимое и достаточное условия экстремума функции двух переменных, найти стационарные точки и экстремумы функции

2. Найти экстремумы функции двух переменных , если переменные связаны условием

3. Найти наибольшее и наименьшее значение функции z=z(x,y), заданной неявно соотношением x+3y‑5z+9=0 в области, ограниченной линиями , , , .

4. С помощью метода Лагранжа найти условные экстремумы функции z=z(x,y) при указанной связи между аргументами. Изобразить ответ и связь между аргументами на плоскости Оху. ,

Вариант 7

1. Применяя необходимое и достаточное условия экстремума функции двух переменных, найти стационарные точки и экстремумы функции

2. Найти экстремумы функции двух переменных , если переменные связаны условием

3. Найти наибольшее и наименьшее значение функции z=z(x,y), заданной неявно соотношением x‑2y+5z+17=0 в области, ограниченной линиями , 1, , .

4. С помощью метода Лагранжа найти условные экстремумы функции z=z(x,y) при указанной связи между аргументами. Изобразить ответ и связь между аргументами на плоскости Оху. ,

Вариант 8