Шпоры по ТерВер не те
.doc|
15.ДСВ и их числ. хар-ки |
38.МоментыСВ.Ассиметрия и эксцесс. |
30. Закон больших чисел в форме теоремы Чебышева |
24.Равном.распред.Матем. ожидание и дисперсия случ величины. |
22.Биноминальный закон распр-ия
|
|
Дискретной назыв. такую СВ множество значений которой конечно или счетное.Пусть ДСВ Х может принимать зн-ия х1 ,х 2…х n . Обозначим рi =Р(Х=Хi), i=1,n. Закон распределения ДСВ задается таблицей распределения или рядом распределения: х
рi р1 р2 ..… рn Графич.изображение ряда распределения назыв.полигоном распред. СВ. Основные хар-ки ДСВ мат.ожидание и дисперсия.
|
Моментом n-го порядка Х по отн-ию к знач-ию а Mn(a)=M(X-a)n, а=0-начальный момент ύn ф=Ь(Ч)-центральный μn Для
ДСВ: ύn= Для
НСВ: ύn= Можно показать что справедлива формула: μn= μ2=ύ2-ύ12 μ3=ύ3-3ύ2 ύ1+2ύ12 μ4=ύ4-4ύ1 ύ3+6ύ12 ύ2-3ύ14 На практике при изуч. распределения отличного от норм. необх. колич. оценить эти различия для этого вводятся вспомог.числ. хар-ки ассиметрия и эксцесс.Центр. момент 3-го порядка μ3 характ-ет отклонение распределения СВХ от симметрии относит. мат.ожид.За меру этого отклонения берут число: α = μ3/σ3(х)-коэф.ассиметрии. Ассиметрия всех распред-ий графики которых симметр. относит.прямой х=а=М(х) равна 0. Центр.момент 4-го порядка μ4 служит для хар-ки крутости распред-ия СВ Х по сравнению с крутостью распред-ия НСВ с мат.ожид.и дисп. такими же как и у Х.За меру этой крутости берут число: χ = [ μ4/σ4(х) ] -3 |
Если случайные величины Хi, i=1,2…,n, независимы и одинак. распределены со средними МХi =a и дисперсиями DXi =DX, то справедлива теорема Чебышева: n P(|1/n сумма ( Xi) - a | <= e ) >= 1- DX/ne*e i=1 Из этого неравенства при n стр-ся к беск-ти следует закон больших чисел n limP(|1/n сумма (Xi )- a| <=e)=1 n-& i=1 Смысл закона закл . в том, что средние значения случайных величин стремятся к их мат. ожиданию при n- & по вероятн. Отклонение средн. значений от мат.ожидания стан-ся сколь угодно малым с вероятностью, близкой к 1, если n достаточно велико или вероятность любого откл. средн. знач. от а сколь угодно мала с ростом n. (e – это эпсилон.) |
Непр. случ. велич.х распред. равномерно на отрезк [а;b], если её плотность вероятности р(х) постоянна на этом отрезке и =0 вне его: 1/ (b-a), а< =х<=b Р(х)= { О, х<а, х>b Функция распред. случайн. величины, расп- ред-ой по равномерн. закону, имеет вид: O, x<=a F(x)= { (x-a)/(b-a), a<x<=b 1, x>b График р(х) иF(х)на рис Мат. ожидание и дисперсия равн. случ. величины: МХ=(а+b)/2; DХ=(b-а)( b-a)/ 12
|
Пусть
проводится n
независимых испытаний. В результате
каждого из которых возможны 2 исхода:
А – успех с вероятностью p,
или
Дискретная
случайная величина X,
которая может принимать только целые
неотрицательные значения с вероятностямиP
(X=m)=
Мат.ожидание
Дисперсия
D(x)=
|
|
8. Теор. умнож. д/произв. числа событий. |
20.Матожидание ДСВ и НСВ. |
31.Теорема БЕРНУЛЛИ |
11. Локальная предельная теорема Муавра-Лапласа |
18. Функция распред-ия ДСВ |
||||||||||
|
Вероятность наступления n событий А1,А2,Аn=произведению вертностей одного из них на условную вероятность каждого последующего события, вычисленного в предположении, что все предыдущие события уже наступили: P(A1,A2…An)=P(A1)*P(A2/A1)*P(A3/A1*A2)*…P(An/A1*A2*…*An-1) События А и В независимы тогда и только тогда, когда вероятность события AB ровна произведению вероятностей событий А и В. свойства
независимых событий:1.если соб.-ия А и
В нез.-ы, то А и
2.если
соб.-ия А и В нез.-ы, то и
|
Мат. ожид-ем СВ Х наз. ∑ по всем исходам знач-й СВ Х, умн-х на их вер-ти:
М.О. НСВ с
плотн-ю распр-я f(х)
наз. число
Геометрический смысл М.О.: М(Х) – это абсц-са центра тяжести криволин-й трап-и, огран-ной граф-м кр. распр-я (полигоном распр-я для ДСВ) и осью ОХ. Св-ва М.О.: 1. Если Х=С=const - СВ, приним-я пост-е знач-е С, то М(С)=С 2. М(С∙Х)= С∙М(Х), С - const
3.М(Х 4. М(Х∙У)=М(Х) ∙ М(У) – незав-е СВ
5. М(Х-М(Х))=0,
где М(Х) – число при
СВ Х - М(Х) наз. отклонением СВ Х от ее М.О.
|
Теорема Бернулли:
Если вер-ть наст-я
соб-я А в каж-м из n
повторных нез-х испыт-й пост-на, то при
неогран-м увел-ии числа n
исп-й отн-я частота
Т-ма Б-ли явл-ся теор-ким обосн-ем для стат-го опр-я вер-ти. Неравенство Бернулли:
Пусть
|
Если вероятность наступления события А в каждом из n независимых испытаний равна p (p0, p1), а число испытаний достаточно велико, то справедлива формула:
где Замечание: формула 2 исп, когда n10, np>10
|
Пусть ДСВ задана табл. распред-ем, тогда
ее ф-ция распределения:
xi x1 x2 … xn pi p1 p2 … pn y=F(x)=P(X<x)=P(X=x1)+…P(X=xn)=p1+…+pn где x1<x2<…<xn<x n F(x)=∑pi => pk=F(xk+1)-F(xk)-ф-ция распред-я однозначно определяет з-н распред-я ДСВ. i=1 Графиком ф-ции распред-я д/ДСВ явл-ся кусочно-постоянная ф-ция. Св-ва ф-ции распред-я: 1.) монотонно не убывает; 2.) непрерывна слева; 3.) limF(x)=0, limF(x)=1 x→-∞ x→+∞
|
|
26.Показательный з-н распред-ия
|
12. Редкие события. Теорема Пуассона.
|
25.Норм.з-н распр-ия. Мат. ожидание и диспер.СВ, распред. по норм. з-ну. |
10.Формула Бернулли |
5.Действия над событиями. Диаграмма Венна |
|
Непрерывная СВ
Х имеет показ. (экспоненциальное)
распределение с параметром λ >0, если
ее плотность распред-я имеет вид:
Ф-ция распределения
СВ, распределенной по показ. з-ну:
Показательному распределению обычно подчиняется величина срока службы различных устройств и времени безотказной работы отдельных элементов этих устройств, другими словами – величина промежутка времени между появлениями двух послед-х редких событий. Вероятность попадания случайной величины Х на интервал (α;β)
Графики ф-ции распределения и плотности вероятности показательного распределения:
|
Ф-ла Pn(m)=(1/√npq)φ((m-np)/√npq) (2) позволяет получать тем более близкие к точному значения Pn(m) результаты, чем больше знач. корня √npq и чем ближе знач . p и q к ½. Если в-сть успеха р по отдельным испытаниям близка к 0 (такие события наз. редкими), то даже при большом n, но малом np (np<10) в-сти, полученные по ф-ле (2) недостаточно близки к их истинным знач. В этом случае прим. другую асимптотическую ф-лу – ф-лу Пуассона. Теорема: Если в-сть наступления события А в каждом из независимых испытаний постоянна, но близка к 0, а np=λ<10, то Pn(m)≈λm(e-λ/m!) (4) Замечание: ф-лу Пуассона исп., когда n≥10 (n≥100), а np≤10.
|
Влияние параметров а и σ на вид нормальной кривой. Нормальное распределение явл. одним из наиболее часто встречающихся. Играет большую роль в тер. вер., поскольку явл. Предельным законом, к к-ому приближаются все др. законы распределения. Док-но, что если знач. СВ возникают в результате большого числа независимых воздействий, ни одно из к-ых не превалирует над остальными, то результат этих воздействий явл. СВ, распределенной по нормальному закону почти всегда. По нормальному закону распределены: случайные ошибки измерения, лин. размеры деталей при массовом пр-ве, биометрические показатели лиц определенного возраста, отклонения в результате хим., спектральных и других анализах. Говорят, что непрерывная СВ Х имеет нормальное распределение с параметрами а и σ, если ее плотность распределения имеет вид -(x- a)2/2σ2 f(x)=( 1/σ√2π) e Определение корректно, т.к.: -∞∫+∞f(x)dx=1 M(X)= -∞∫+∞xf(x)dx=a σ (X)= -∞∫+∞(x-M(X))2f(x)=σ2 Для геометрической интерпретации параметров а и σ исследуют поведение ф-ии -(x-a)2/2σ2 f(x)=( 1/σ√2π) e график к-ой наз. нормальной кривой. График симметр.относит.а При изменении параметра а форма кривой не меняется, а ее график сдвигается влево или вправо. При изменении параметра σ меняется форма нормальной кривой: с увеличением параметра σ кривая должна приближаться к 0Х и растягиваться вдоль этой оси, а с уменьшением σ кривая стягивается к прямой х=а.
|
Пусть проводится n независимых испытаний, в результате каждого из к-ых возможны 2 исхода: может произойти событие А(успех) с вер-тью р или не произойти событие А с вер-тью q = 1-p. Пусть X – число успехов в n испытаниях, тогда справедлива ф-ла Бернулли: Р(Х=m) = Рn(m) = CmnРmQn-m Док-во: Пусть проведено n независимых испытаний, в рез-те к-ых событие А произошло m раз (не важно в каком порядке). Это означ-т, что произошло событие С = { А произошло m раз, Ă произошло n-m раз}. Т.к. все n события независимы, то вер-ть события С Р(С) = Рm Qn-m. Однако событ. А может появиться в n опытах и совершенно др. послед-ти и число таких послед-ей = Cmn.ВсеCmnвариантов появления событ. А m раз предст-т собой несовместн. событие с вер-ми Рm * Qn-m, поэтому справедлива ф-ла Бернулли. Наиболее вероятное число успехов в схеме испытаний Бернулли удовл-т нер-ву: (n+1)p-1 ≤ m ≤ (n+1)p
|
Пусть некоторому опыту G соот-т простр-во элем-ых событий Ω, кот. изображ-ся в виде квадрата един-й площади. Вводимые далее действия над событиями м/представить также как операции над множ-ми и проиллюстр-ть с помощью диаграмм Венна. Будем
говорить, что соб. А влечет за собой
соб.В, если из наступления А следует
наступление В.(
Суммой(объединением)
соб.А и В наз. такое соб. С, кот. происходит
т. и т.т., когда происх-т по крайне мере
1 из соб-й А и В.( Разностью соб. А и В наз. соб. С, кот. происходит т. и т.т., когда А происх-т, а В не происх-т.(С=А-В; С=А\В) Произведением(пересечением) соб.А и В наз. С, кот. происходит т. и т.т., когда происходит А и В. (С=А*В; С=А∩В) Соб. А и В наз. несовместными (не пересекающимися), если они не м/произойти одновременно, т.е. А*В=ǿ Соб. В наз. противоположным к соб.А (дополнительным к А)[В= Ă], если оно происходит т. и т.т., когда А не происходит.(В=Ă)В рез-те опыта G 1 из 2-х соб-й А и Ă обязательно произойдет и эти события не совместны.( А+Ă= Ω; А*Ă= ǿ) Говорят,
что соб-я образуют полную
группу(попарно
несовместных) событий если: а)в рез-те
G
одно из них обязательно произойдет
|
|
2. Случ. события. Вероят-ть: статистич-ое определение. |
3. Пространство элементарных событий |
4. Вероятность: геом. опр. Задача о встрече
|
6. Т. сложения вероятностей. |
7. Условная вер-сть. Т.* вер-тей |
|
Опыт - осущ-ие заданного комплекса условий (G). Исход испытания - событие (А, В, С). События бывают детерминированные (подчинены жесткой связи причина-следствие) и недетерминированные. Случайное событие – это событие, которое м/произойти и не произойти в результате опыта G. Пусть в связи с некот. оп. G нас интересует наступление случайного события A, проводим n-испытаний, пусть при этом соб. А произошло m-раз, m≤n.
Число
Есть события д/к-рых относ. частоты обладают опред-го рода устойчивостью: при больших n они стабилизируются около некоторого пост-го р. Это число – вероятность события А. Статистическое определение вероятности заключается в том, что за вероятность события А принимается постоянная величина, вокруг которой колеблются значения частостей при неограниченном возрастании числа n.
|
События, которые нельзя разложить на составляющие их события, называются элементарными. Любое событие А из пространства достоверных событий можно составить из элементарных событий. Совокупность всех эл. событий в опыте называется пространством эл. событий. Классическое определение вероятности Классической схемой, или схемой случаев, называется опыт, при к-ром число элем. исходов конечно и все из них равно возможны. Элементарное событие (исход) называется благоприятным д/события А, если его появление влечет наступление события А (т.е. эл.событие входит в число элементов, составляющих А).
К
Из определения вероятности следует, что Р(Ø) = 0
|
В случае бескон. кол-ва равновозможных эл. исходов оп. G пространство элементарных событий часто м. представить в виде некоторого мн-ва Ω в простр-ве (одномерное пространство R-прямая; двумерное-R). Элемен. событие есть (.)-ки заполняющие мн-во Ω, тогда любому событию А соот-ет некоторое подмн-во мн-ва Ω. Геом.вероятностью соб.А наз-ся отношение объема мн-ва А к объему всего мн-ва Ω. P(A)=V(A) / V(Ω) 0≤P(A)≤ 1 Таким образом представим след. ситуация: бросаем наугад точку в обл. Ω (стреляем по Ω) попадание в мн-во А означает, что произошло событие А Замечание: В дальнейшем пр-во эл.событий Ω будем изобр. в виде прямоуг. если это прямоуг. единич. площади то очевидно P(A)=S(A)/S(Ω)=S(A) Задача о встрече: 2 студента договорились встретиться. Каждый из них приходит в течение 1 ч. и ждет 20 мин. Какова вероят. их встречи? Опишем пр-во эл. соб.: Пусть x- время прихода 1 студ., y- время прихода 2-го студ. Тогда 0≤x≤1ч. и 0≤y≤1ч.; в кач-ве Ω м. рассматривать квадрат. Событие А={студ.встретятся}={|x-y|<1/3} |x-y|<1/3 ‹=› -1\3<x-y<1\3 y=x+1/3 y=x-1/3 P(A)=S(A)/S (Ω)=1-2\3*2\3=5\9 |
Пусть нек-ому опыту G соотв-т простр-во элемент-ых соб. Ω; , кот-ое будем изобр-ть в виде квадрата единичной площади. P(A)=S(A). 1.Теорема сложения вер-ей Вер-ть суммы 2-х соб. равна сумме вер-ей этих соб. без вер-ти их произведения. P(A+B)=P(A)+P(B)-P(AB) Следствие: 1)для несовместных событий: P(A+B)=P(A)+P(B); 2)для полной группы соб. H1,+,Hn: P(H1+…+Hn)=P(Ω)=1 3)сумма вер-ей противополож. соб. Равна 1: P(A)+P(A)=1; P(A)=1-P(A) 2.Вероятность разности 2-х соб. P(A-B)=P(A)-P(AB)
|
1) Условная вероятность события А при условии В равна Р(А/B)=P(A*B)/P(B), Р(В)>0. 2) Событие А не зависит от события В, если Р(А/B)=P(A). Независимость событий взаимна, т.е. если событие А не зависит от В, то событие В не зависит от А. В самом деле при Р(А)>0 имеем Р(B/A)=P(A*B)/P(A)=P(A/B)*P(B)/P(A)=P(A)*P(B)/P(A)=P(B). Вытекает следующая формула умножения вероятностей: Р(А*В)=Р(А)*Р(В/A). Для независимых событий вероятность произведения событий равна произведению их вероятностей: Р(А*В)=Р(А)*Р(В). 3) События А1,А2,…,Аn образуют полную группу событий, если они попарно несовместны и вместе образуют достоверное событие, т.е. Аi*Aj=0, i не=j, U по i от 1 до n Аi=омега. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: Р(АВ)=Р(А)*Ра(В). В частности для независимых событий Р(АВ)=Р(А)*Р(В), т.е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.
|
|
9. Формула полной вероятности. |
17.Функция распред СВ |
13. Интегральная теорема Муавра-Лапласа |
14.Понятие СВ |
19. Ф-ция распред-я НСВ.
|
|
Систему событий А1, А2, ...,AN называют конечным разбиением (или просто разбиением), если они попарно несовместны, а их сумма образует полное пространство событий: А1 + А2 + ... + АN =
Если события Аi
образуют разбиение пространства
событий и все P(Ai)
> 0, то для любого события В имеет
место формула полной вероятности:
P(B)
= что непосредственно следует из (8.2.14) для попарно несовместных событий: B = B = BA1+BA2+...BAN. P(B) = P(BA1)+P(BA2)+... +P(BAN) = P(A1)P(B/A1)+P(A2)P(B/A2)+...+P(AN)P(B/AN). Пусть известен результат опыта, а именно то, что произошло событие А. Этот факт может изменить априорные (то есть известные до опыта) вероятности гипотез. Для переоценки вероятностей гипотез при известном результате опыта используется формула Байеса
|
Функцией распределения случайной величины Х называется функция FX(x)= P{X<x}, xR Под {X<x}понимается событие, состоящее в том, что случайная величина Х принимает значение меньшее, чем число х. Если известно, о какой случайной величине идёт речь, то индекс, обозначающий эту случайную величину, опускается: F(x) FX(x). Как числовая функция от числового аргумента х, функция распределения F(x) произвольной случайной величины Х обладает следующими свойствами: 1)для любого xR: 0 F(x) 1 2) F(-) = limx F(x) = 0 ; F(+) = limx F(x) = 1; 3) F(x)-неубывающая функция, т.е.для любых α,βтаких, что α< β :F(β) - F(α); 4)непрерывна слева
|
Если число повторных независимых испытаний достаточно велико, вероятность появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что в этих испытаниях событие А появится число раз, заключенное в границах [a;b], может быть посчитана по формуле:
Функция нечетная, возрастающая X>4, Ф(х)=1 Следствие из интегральной теоремы Муавра-Лапласа. Если число повторных независимых испытаний достаточно велико, вероятность появления события А в каждом испытании постоянно и отлично от нуля и единицы, то вероятность того, что число появлений события А отклонится от произведения np не больше, чем на некоторое положительное число r по модулю, может быть посчитано по формуле
|
Случайной величиной назыв числ величина, к-ая в результате опыта может принять какое-либо знач из некоторого мн-ва, причем заранее, до проведения опыта, невозможно сказать, какое именно знач она примет.СВ обознач буквами X, Y, Z,..., а их возможные значения —х, у, z. СВ назыв дискретной, если множество ее значений конечно или счетно, и непрерывной в противном случае. Законом распред.СВ назыв любое соотношение, связыв возможные знач этой СВ и соответс им вероятности. Закон распределения ДСВ задается чаще всего не функцией распределения, а рядом распределения, т.е, таблицей В которой x1, x2, ..., xn, ... - расположенные по возрастанию значения ДСВ X, а р1, р2, ..., рп, ... — отвечающие этим значениям вероятности: pi = Р{Х = хi), i= 1, 2, ..., п, ... . Очевидно, pi= 1. Полигоном распред ДСВ X назыв ломаная, соединяющая точки {xi;pi), расположенные в порядке возрастания хi. |
Судить о хар-ре распр-ия в небольшой окрестности точек числ. оси позвол-т плотность распределения вер-ей. Рассм-м НСВ Х с интегр.непр-но диф-ой ф-ией распр-ия F(x). Вер-ть попад-ия этой вел-ны в интервал (х,х+∆х) равна Р(х<X<x+∆x)=F(x+∆x)-F(x). Вер-сть, к-рая находится на ед-цу длины рассмарт-го интервала: (Р(х<X<x+∆x))/∆x=(F(x+∆x)-F(x))/∆x.
Если мы перейдем
к пределам, то получим вер-ть, кот.
прих-ся на изолиров-ую точку Х:
f(x)=F’(x). График ПР вер-тей – кривой распр-ия CВ Х. Cв-ва ПР: 1.f(x)≥0 для люб.x – cв-во неотриц-ти.
3.
Cв-во нормировки.
|




 i
х1
х2
…. хn
i
х1
х2
…. хn

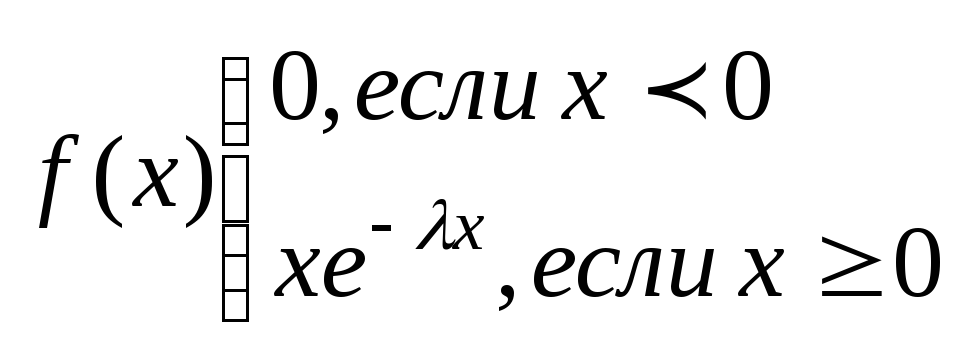
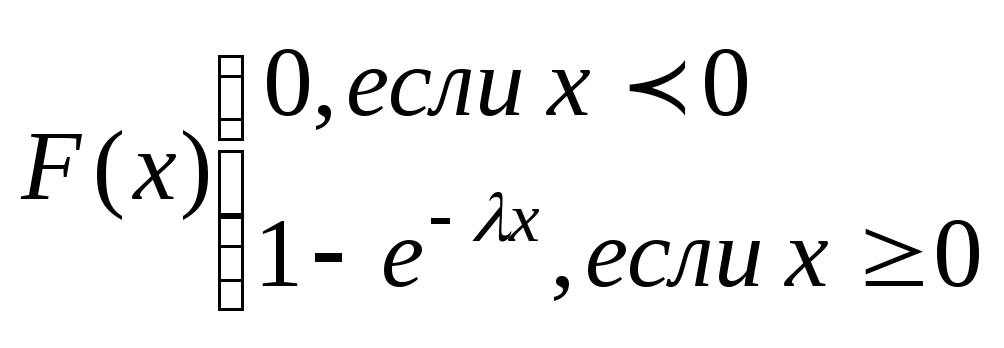
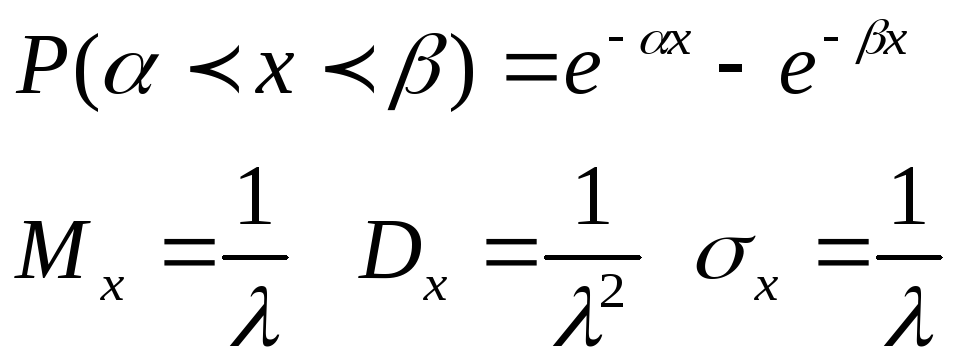
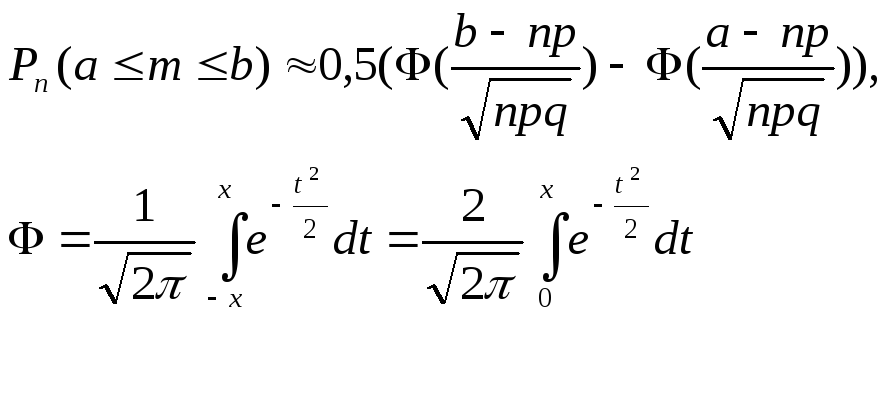 Свойства функции
Лапласа:
Свойства функции
Лапласа: