1. Синтез комбінаційних схем

В багатьох залізничних пристроях використовується багато комбінаційних схем. Комбінаційні схеми – це логічні схеми, сигнал на виході яких у кожен момент часу визначається комбінацією вихідних сигналів у той же момент часу.

Поняття функції алгебри логіки (ФАЛ) є базовим у алгебрй логіки – математичному апараті, який використовується для опису умов функціювання, а також при перетворенні структур дискретних автоматів.

Головні аксіоми алгебри логіки, а також тотожні співвідношення, отримані на їх основі, дозволяють перетворювати логічні формули, не порушуючи еквівалентності ФАЛ.

Бульова алгебра базується на кількох аксіомах, з яких одержують основні закони перетворень ФАЛ.

Ось деякі з них:

1)Асоціативний:

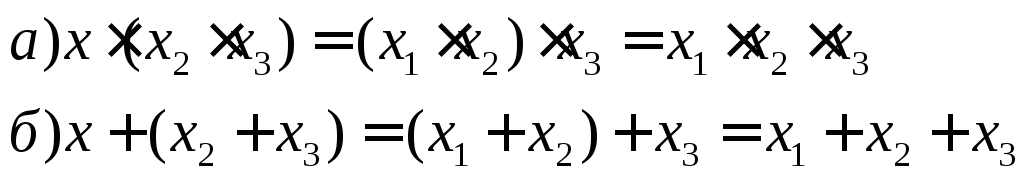
2)Звернення:

якщо , то

3)Подвійної інверсії (заперечення):

4)Інверсії (правило де Моргана):

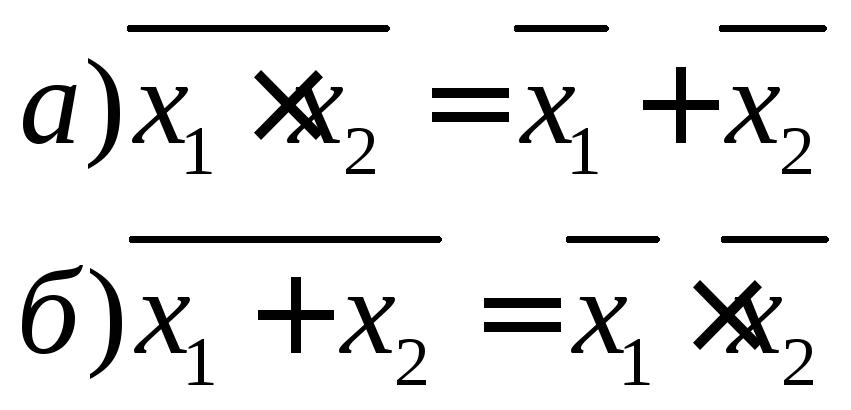
Для того щоб синтезувати комбінаційні схеми треба побудувати таблицю істинності, потім перейти від табличного способу завдання функції алгебри логіки (ФАЛ) до її запису у вигляді нормальних форм подання ФАЛ: досконалої диз'юнктивної нормальної форми (ДДНФ) і досконалої

6

кон’юнктивной нормальної форми (ДКНФ),і побудувати карту Карно.

Є кілька нормальних форм подання ФАЛ. Наприклад дві з них: ДДНФ і ДКНФ. Щоб знайти ДДНФ вибирають із таблиці тільки ті рядки, у яких стоять набори змінних, що перетворюють функцію в 1. При цьому, якщо аргумент входитьдо даного набору як 1, він записується в кон’юнкцію (логічне множення) без зміни (). Якщо ж входить у набір як 0, то у відповідну кон’юнкцію вписується його заперечення().З'єднуючи ці кон’юнкції знаками диз'юнкції (логічне додавання) остаточно одержуємо ДДНФ.

Для знаходження ДКНФ вибирають із таблиці тільки ті рядки, у яких стоять набори змінних, що перетворюють функцію в 0. При цьому, якщо аргумент входить у даний набір як 0, він уписується в диз'юнкцію без зміни (x_i). Якщо ж x_i входить у набір як 1, то у відповідну диз'юнкцію вписується його заперечення ().З'єднуючи ці диз'юнкції знаками кон’юнкції остаточно одержуємо ДКНФ.

Якщо більшість значень функції одиничні, то її буде зручніше записувати в ДКНФ.

Карта Карно являє собою двокоординатну таблицю, у якій кожній клітинці поставлені у відповідність набори значенні змінних логічної функції. Набори, подані сусідніми клітинками, відрізняються значеннями тільки однієї змінної. Сусідніми називаються дві клітинки, які знаходяться поряд, розташовані в одному рядку або стовпці. Сусідніми також вважаються клітинки розташовані по кінцям кожного стовпця або рядка: нижня клітка в будь-якому стовпці є сусідньою по відношенню до верхньої клітинки того ж стовпця, а права клітка будь-якого рядка є сусідньої відносно лівої клітинки того ж рядка.

Карта Карно містить k=2ⁱ клітинок ( i- кількість змінних даної логічної

функції), що дорівнює кількості рядків у таблиці істинності функції або

7

числу одиничних наборів змінних ДДНФ і нульових наборів змінних ДКНФ, разом узятих.

Властивість сусідства в карті Карно зручно використати для групування окремих одиничних наборів (коньюнктивних термів) у підкуби бо об'єднання з 2ⁿ одиничних наборів (n=0,1,2,3,4,…). Підкуби творяться з метою виключення однієї, двох, або декількох змінних, вхідних в одиничні набори, тому що при склеюванні відбувається виключення однієї або декількох змінних.

Мінімізацією ФАЛ називається процес скорочення кількості входжень незалежних змінних й операцій в аналітичні вираження для ФАЛ.

Щоб визначити внесок підкуба в мінімальну функцію, необхідно взяти диз'юнкцію або кон’юнкцію одиничних наборів змінних, що входять до підкуба. Існують мінімальна диз'юнктивна нормальна форма (МДНФ) і мінімальна кон’юнктивна нормальна форма (МКНФ).

Утворюючи підкуби для отримання мінімального значення функції треба дотримуватися таких правил:

• утворити двоклітинкові підкуби з наборів, які мають тільки одного сусіда;

• із наборів, що залишились, утворити підкуби максимальної величини ( якщо це можливо ), які не перетинаються ;

• з наборів, що залишились, утворити підкуби максимального розміру, які перетинаються;

• з наборів, що не мають жодного сусіда, утворити одноклітинкові підкуби;

• закінчити утворення підкубів, якщо всі набори задіяні.

При використанні цього потрібно строго дотримуватися послідовності виконання пунктів.

1. Синтез комбінаційних схем у базисах

Базис – це сукупність логічних елементів, що реалізують функції

8

відповідній теоремі про функціональну повноту.Базис має від одного до шести входів, а вихід тільки один. Прикладами найпоширеніших базисів є:

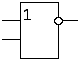
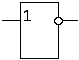
І І-НІ АБО АБО-НІ НІ

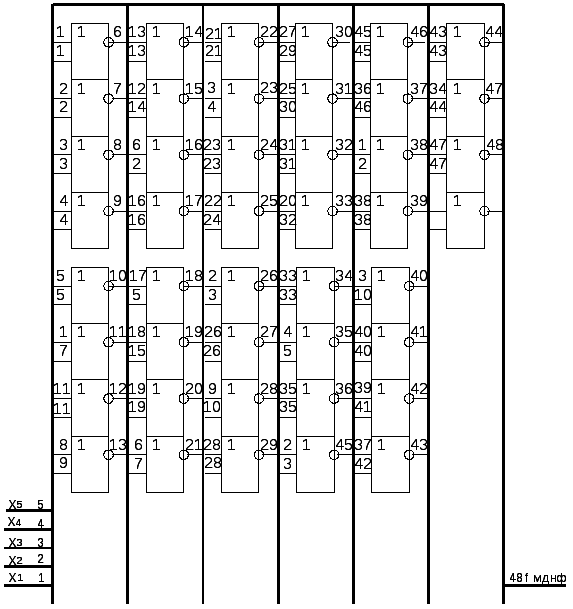
У складі різних інтегральних мікросхем є елементи, що утворять названі базиси. В моїй роботі буде використовуватися мікросхема марки 1533ЛЕ1, яка має вигляд:

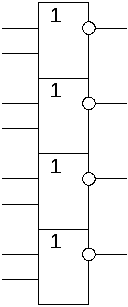
Синтез комбінаційних схем має чотири етапи:

• утворення таблиці істинності для ФАЛ, що описує роботу проектованої логічної схеми (найчастіше на підставі словесного опису принципу роботи);

• утворення математичної формули для ФАЛ, що описує роботу синтезованої схеми, у вигляді ДДНФ або ДКНФ (на підставі таблиці істиності);

• аналіз отриманої ФАЛ з метою побудови різних варіантів її математичного виразу й знаходження найкращого з них у відповідності з тим чи іншим критерієм;

• утворення функціональної (логічної) схеми пристрою з елементів, які складають вибраний базис.

9

F₃₉={0,1,3,14,15,16,18,19,20,21,22,24,25}_x1x2x3x4x5

Таблиця 1

№	Х1	Х2	Х3	Х4	Х5	F
0	0	0	0	0	0	1
1	0	0	0	0	1	1
2	0	0	0	1	0	0
3	0	0	0	1	1	1
4	0	0	1	0	0	0
5	0	0	1	0	1	0
6	0	0	1	1	0	0
7	0	0	1	1	1	0
8	0	1	0	0	0	0
9	0	1	0	0	1	0
10	0	1	0	1	0	0
11	0	1	0	1	1	0
12	0	1	1	0	0	0
13	0	1	1	0	1	0
14	0	1	1	1	0	1
15	0	1	1	1	1	1

16	1	0	0	0	0	1
17	1	0	0	0	1	0
18	1	0	0	1	0	1
19	1	0	0	1	1	1
20	1	0	1	0	0	1
21	1	0	1	0	1	1
22	1	0	1	1	0	1
23	1	0	1	1	1	0
24	1	1	0	0	0	1
25	1	1	0	0	1	1
26	1	1	0	1	0	0
27	1	1	0	1	1	0
28	1	1	1	0	0	0
29	1	1	1	0	1	0
30	1	1	1	1	0	0
31	1	1	1	1	1	0

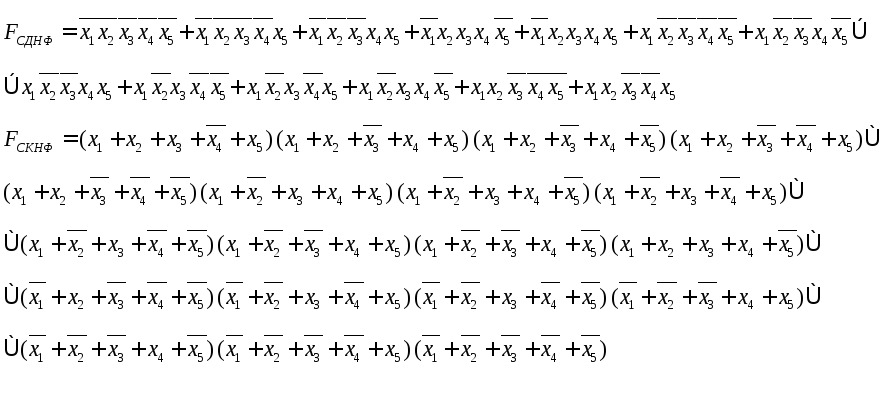
10

Малюнок 1

12

8

11

6

1

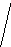
1						1	1
		1			1
1							1
1	1	1	1	1		1

9

3

7

10

13

5

4

2

14

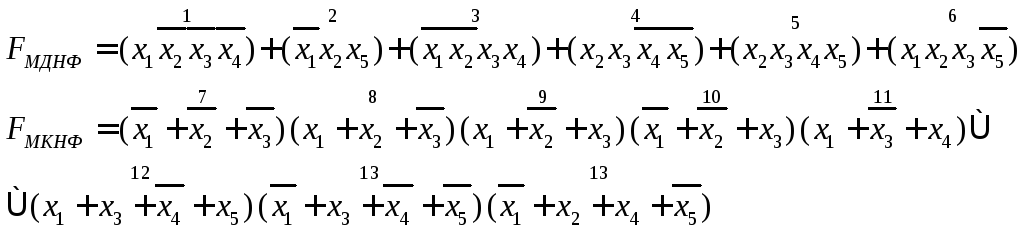
11

12

Малюнок 2