2.2. Реверсивний чотирьох розрядний регістр зсуву (ап2)
Регистр зсуву – схема, яка складається зі звязаних між собою 1-бітових елементів памяті, які розміщені в єдиному корпусі.
На
прикладі розглянемо реверсивний 4-x-
розрядний
регістр здвигу, який побудуємо за
допомогою 
тригерів і на мікросхемі 1533ЛЕ1
Спочатку
будуємо функціональну таблицю (Таблиця
2.21), використовуючи таблицю збудження
тригерів (Таблиця 2.11). Розглядаємо, що
А ділить таблицю на дві частини, в якій
перша частина показує, що ми виконуємо
здвиг вправо, а друга-здвиг вліво; х -
вхідний сигнал; t
- початковий момент часу; (t+1)
– наступний такт (момент часу); координати
у1,у2,у3,у4
– внутрішній стан автомату; Z1,Z2,Z3,Z4
– вихідні сигнали.
|
A |
X |
t |
t+1 |
Тригери |
Z1 |
Z2 |
Z3 |
Z4 | |||||||||||||
|
y1 |
y2 |
y3 |
y4 |
y1 |
y2 |
y3 |
y4 |
|
|
|
|
|
|
|
| ||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
~ |
1 |
~ |
1 |
~ |
1 |
~ |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
~ |
1 |
~ |
1 |
~ |
1 |
0 |
0 |
0 |
0 |
1 |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
~ |
1 |
~ |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
~ |
1 |
~ |
1 |
0 |
~ |
1 |
0 |
0 |
1 |
1 |
|
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
~ |
1 |
0 |
0 |
1 |
1 |
~ |
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
~ |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
~ |
1 |
0 |
~ |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
~ |
1 |
0 |
~ |
1 |
~ |
1 |
0 |
1 |
1 |
1 |
|
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
~ |
1 |
~ |
1 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
~ |
1 |
0 |
1 |
0 |
0 |
1 |
|
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
~ |
1 |
1 |
0 |
1 |
1 |
|
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
~ |
1 |
0 |
1 |
1 |
~ |
1 |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
~ |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
~ |
1 |
~ |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
~ |
1 |
~ |
1 |
~ |
1 |
1 |
1 |
1 |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
~ |
1 |
~ |
1 |
~ |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
~ |
1 |
~ |
1 |
0 |
0 |
0 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
~ |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
~ |
1 |
0 |
~ |
1 |
0 |
0 |
1 |
1 |
|
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
~ |
0 |
1 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
~ |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
~ |
1 |
~ |
1 |
0 |
1 |
1 |
1 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
~ |
1 |
0 |
1 |
1 |
~ |
1 |
~ |
1 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
~ |
1 |
0 |
1 |
1 |
~ |
1 |
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
~ |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
~ |
1 |
0 |
1 |
1 |
0 |
~ |
1 |
1 |
0 |
1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
~ |
1 |
~ |
1 |
0 |
1 |
1 |
~ |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
~ |
1 |
~ |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
|
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
~ |
1 |
~ |
1 |
~ |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
~ |
1 |
~ |
1 |
~ |
1 |
~ |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
~ |
1 |
~ |
1 |
~ |
1 |
~ |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
~ |
1 |
~ |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
~ |
0 |
1 |
1 |
0 |
1 |
~ |
0 |
0 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
~ |
01 |
1 |
~ |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
~ |
1 |
~ |
0 |
1 |
0 |
0 |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
|
1 |
0 |
00 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
~ |
1 |
1 |
0 |
1 |
~ |
00 |
1 |
1 |
0 |
|
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
~ |
1 |
~ |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
|
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
~ |
1 |
~ |
1 |
~ |
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
~ |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
~ |
1 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
01 |
1 |
~ |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
|
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
~ |
1 |
1 |
0 |
1 |
~ |
1 |
~ |
1 |
1 |
0 |
0 |
|
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
~ |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
~ |
1 |
~ |
1 |
1 |
0 |
1 |
~ |
1 |
1 |
1 |
0 |
|
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
~ |
1 |
~ |
1 |
~ |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
~ |
1 |
~ |
1 |
~ |
0 |
1 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
~ |
1 |
~ |
0 |
1 |
~ |
1 |
0 |
0 |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
~ |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
~ |
01 |
1 |
~ |
1 |
~ |
1 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
~ |
0 |
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
~ |
1 |
0 |
1 |
0 |
1 |
|
11 |
11 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
11 |
0 |
1 |
~ |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
~ |
1 |
~ |
1 |
~ |
1 |
0 |
1 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
~ |
1 |
~ |
0 |
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
~ |
0 |
1 |
~ |
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
01 |
1 |
~ |
1 |
~ |
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
~ |
1 |
1 |
0 |
1 |
~ |
0 |
1 |
1 |
1 |
0 |
0 |
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
~ |
1 |
1 |
0 |
0 |
1 |
~ |
1 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
~ |
1 |
~ |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
~ |
1 |
~ |
1 |
~ |
1 |
~ |
1 |
1 |
1 |
1 |
1 |
Таблиця 2.21
За допомогою цієї функціональної таблиці будуємо карти Карно, визначаємо відповідні підкуби, їх внески і приводимо до базису Пірса.
|
y2y3y4 A |
000 |
010 |
110 |
100 |
101 |
111 |
011 |
001 |
|
000 000 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
010 |
|
|
|
|
|
|
|
|
|
110 |
1 |
1 |
|
|
|
|
1 |
1 |
|
100 |
1 |
1 |
|
|
|
|
1 |
1 |
|
101 |
1 |
1 |
~ |
~ |
~ |
~ |
1 |
1 |
|
111 |
1 |
1 |
~ |
~ |
~ |
~ |
1 |
1 |
|
011 |
~ |
~ |
~ |
~ |
~ |
~ |
~ |
~ |
|
001 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
xy1
|
y2y3y4 Axy1 |
000 |
010 |
110 |
100 |
101 |
111 |
011 |
001 |
|
000 000 |
~ |
~ |
~ |
~ |
~ |
~ |
~ |
~ |
|
010 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
110 |
~ |
~ |
1 |
1 |
1 |
1 |
~ |
~ |
|
100 |
~ |
~ |
1 |
1 |
1 |
1 |
~ |
~ |
|
101 |
|
|
1 |
1 |
1 |
1 |
|
|
|
111 |
|
|
1 |
1 |
1 |
1 |
|
|
|
011 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
001 |
|
|
|
|
|
|
|
|
|
y2y3y4 Axy1 |
000 |
010 |
110 |
100 |
101 |
111 |
011 |
001 |
|
000 000 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
010 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
110 |
1 |
|
~ |
1 |
1 |
~ |
|
1 |
|
100 |
1 |
|
~ |
1 |
1 |
~ |
|
1 |
|
101 |
1 |
|
~ |
1 |
1 |
~ |
|
1 |
|
111 |
1 |
|
~ |
1 |
1 |
~ |
|
1 |
|
011 |
|
|
~ |
~ |
~ |
~ |
|
|
|
001 |
|
|
~ |
~ |
~ |
~ |
|
|
|
y2y3y4 Axy1 |
000 |
010 |
110 |
100 |
101 |
111 |
011 |
001 |
|
000 000 |
~ |
~ |
|
|
|
|
~ |
~ |
|
010 |
~ |
~ |
|
|
|
|
~ |
~ |
|
110 |
~ |
1 |
1 |
|
|
1 |
1 |
~ |
|
100 |
~ |
1 |
1 |
|
|
1 |
1 |
~ |
|
101 |
~ |
1 |
1 |
|
|
1 |
1 |
~ |
|
111 |
~ |
1 |
1 |
|
|
1 |
1 |
~ |
|
011 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
001 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
Axy1 |
000 |
010 |
110 |
100 |
101 |
111 |
011 |
001 |
|
000 000 |
1 |
1 |
~ |
|
|
~ |
1 |
1 |
|
010 |
1 |
1 |
~ |
|
|
~ |
1 |
1 |
|
110 |
1 |
1 |
1 |
1 |
|
~ |
~ |
|
|
100 |
1 |
1 |
1 |
1 |
|
~ |
~ |
|
|
101 |
1 |
1 |
1 |
1 |
|
~ |
~ |
|
|
111 |
1 |
1 |
1 |
1 |
|
~ |
~ |
|
|
011 |
1 |
1 |
~ |
|
|
~ |
1 |
1 |
|
001 |
1 |
1 |
~ |
|
|
~ |
1 |
1 |
y2y3y4
|
y2y3y4 Axy1 |
000 |
010 |
110 |
100 |
101 |
111 |
011 |
001 |
|
000 000 |
~ |
|
1 |
1 |
1 |
1 |
|
~ |
|
010 |
~ |
|
1 |
1 |
1 |
1 |
|
~ |
|
110 |
~ |
|
|
~ |
1 |
1 |
1 |
1 |
|
100 |
~ |
|
|
~ |
1 |
1 |
1 |
1 |
|
101 |
~ |
|
|
~ |
1 |
1 |
1 |
1 |
|
111 |
~ |
|
|
~ |
1 |
1 |
1 |
1 |
|
011 |
~ |
|
1 |
1 |
1 |
1 |
|
~ |
|
001 |
~ |
|
1 |
1 |
1 |
1 |
|
~ |
|
y2y3y4 A |
000 |
010 |
110 |
100 |
101 |
111 |
011 |
001 |
|
000 000 |
1 |
|
|
1 |
1 |
~ |
~ |
1 |
|
010 |
1 |
|
|
1 |
1 |
~ |
~ |
1 |
|
110 |
|
|
|
|
~ |
~ |
~ |
~ |
|
100 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
101 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
111 |
|
|
|
|
~ |
~ |
~ |
~ |
|
011 |
1 |
|
|
1 |
1 |
~ |
~ |
1 |
|
001 |
1 |
|
|
1 |
1 |
~ |
~ |
1 |
xy1
|
y2y3y4 Axy1 |
0 |
010 |
110 |
100 |
101 |
111 |
011 |
001 |
|
000 000 |
~ |
1 |
1 |
~ |
|
1 |
1 |
|
|
010 |
~ |
1 |
1 |
~ |
|
1 |
1 |
|
|
110 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
100 |
~ |
~ |
~ |
~ |
|
|
|
|
|
101 |
~ |
~ |
~ |
~ |
|
|
|
|
|
111 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
011 |
~ |
1 |
1 |
~ |
|
1 |
1 |
|
|
001 |
~ |
1 |
1 |
~ |
|
1 |
1 |
|
00
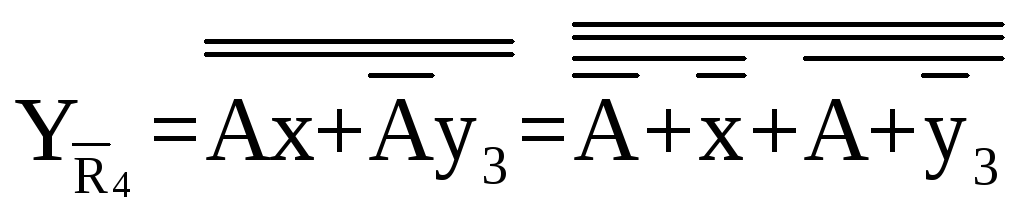
Схема
регістру зображена
на рисунку 2.21
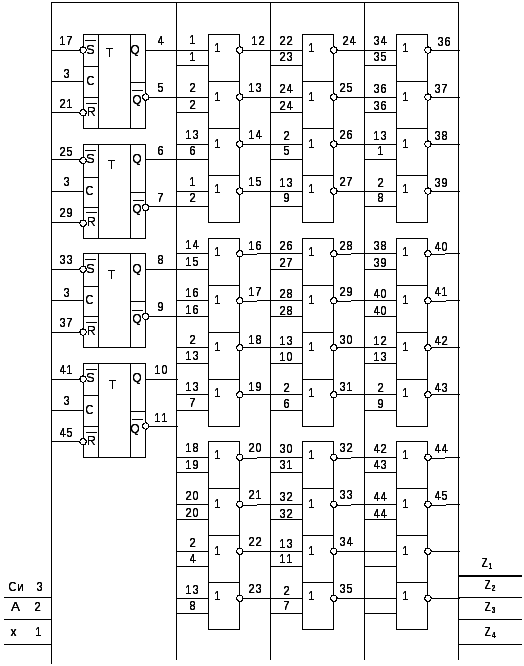
Рисунок 2.21