
2.2 Чотирьох – розрядний регістр зсуву в ліво (ап-2)
В даному курсовому проекті розглядається чотирьох розрядний регістр зсуву в ліво.
Регістри зсуву – це схеми, які складається із зв’язаних між собою одно бітових елементів пам’яті, розташованих в одному корпусі, які пов’язані між собою таким чином, що вихід одного являється входом другого. Входи і виходи зв’язані таким чином , щоб забезпечувати тимчасове зберігання даних та перетворення даних із послідовного в паралельний і навпаки.
Крім регістра зсуву в ліво є регістр зсуву в право і реверсивний регістр.
При подачі сигналу на регістр зсуву вліво код зміщується вліво на один розряд, а на місці молодшого розряду записується цей імпульс.
Даний регістр зсуву необхідно реалізувати
на н е
RS тригері і логічних
елементах Шефера, які складаються в
мікросхему.
е
RS тригері і логічних
елементах Шефера, які складаються в
мікросхему.
Потім будуємо функціональну таблицю (таблиця 2.1) і визначаємо які сигнали потрібно подавати на входи -тригерів для одержання необхідного результату.
Таблиця 8- Збудження тригерів
|
X |
t |
t+1 |
тригери |
|||||||||||||
|
Y1 |
Y2 |
Y3 |
Y4 |
Y1 |
Y2 |
Y3 |
Y4 |
YS1 |
YR1 |
YS2 |
YR2 |
YS3 |
YR3 |
YS4 |
YR4 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
~ |
1 |
~ |
1 |
~ |
1 |
~ |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
~ |
1 |
~ |
0 |
1 |
1 |
0 |
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
~ |
0 |
1 |
1 |
0 |
1 |
~ |
|
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
~ |
0 |
1 |
~ |
1 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
~ |
1 |
~ |
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
~ |
1 |
1 |
0 |
1 |
~ |
|
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
~ |
1 |
~ |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
~ |
1 |
~ |
1 |
~ |
|
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
~ |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
~ |
|
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
~ |
1 |
1 |
0 |
|
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
~ |
1 |
1 |
0 |
1 |
~ |
1 |
~ |
|
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
~ |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
~ |
1 |
~ |
1 |
1 |
0 |
1 |
~ |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
~ |
1 |
~ |
1 |
~ |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
~ |
1 |
~ |
1 |
~ |
0 |
1 |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
~ |
1 |
~ |
0 |
1 |
~ |
1 |
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
~ |
0 |
1 |
1 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
~ |
0 |
1 |
~ |
1 |
~ |
1 |
|
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
~ |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
~ |
1 |
|
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
~ |
1 |
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
~ |
1 |
~ |
1 |
~ |
1 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
~ |
1 |
~ |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
~ |
0 |
1 |
~ |
1 |
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
~ |
1 |
~ |
1 |
|
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
~ |
1 |
1 |
0 |
1 |
~ |
0 |
1 |
|
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
~ |
1 |
1 |
0 |
0 |
1 |
~ |
1 |
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
~ |
1 |
~ |
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
~ |
1 |
~ |
1 |
~ |
1 |
~ |
1 |
Будуємо карти Карно й одержуємо функції
для кожного входу кожного тригера.
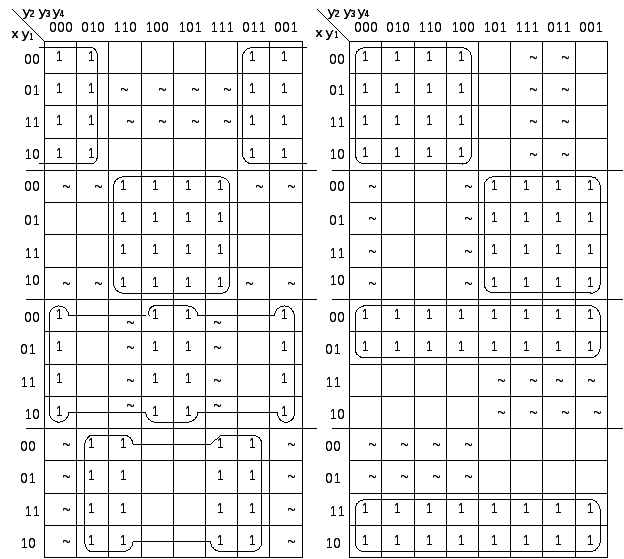
Перетворюємо отримані функції, щоб можна було реалізувати їх на базисі Шефера, за допомогою правила Деморгана.
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
Схема чотирьох - розрядного регістра зсуву вліво наведена в доданку Е.
2.3 Реверсивний двійковий лічильник, працюючий в коді Грея з М=12
Лічильники використаються для керування
послідовністю операцій. Вихідні сигнали
тригерів, що входять у лічильник
розглядаються спільно, визначаючи при
цьому стан лічильника в цілому. В даній
курсовій роботі використовується чотири
розрядний реверсивний лічильник, при
подачі нуля лічильник зсувається вліво,
а при подачі одиниці - вправо. Отже
спочатку складаємо карту Карно  для
коду Грея, в ній кожний наступний код
відрізняється від попереднього тільки
одним розрядом:
для
коду Грея, в ній кожний наступний код
відрізняється від попереднього тільки
одним розрядом:
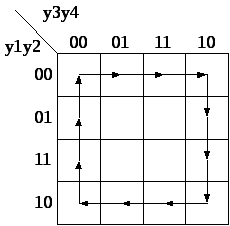
Будуємо граф переходів сигналів:
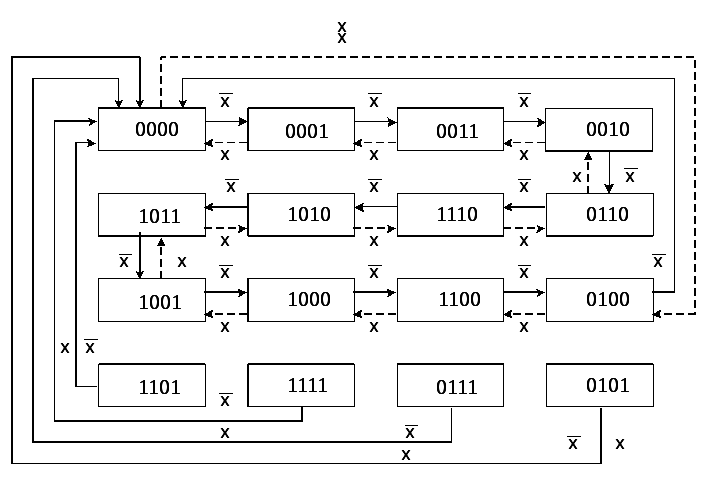
Визначаємо, що для реалізації даної схеми потрібно 4 тригери. За завданням використаємо не RS-тригери. Потім будуємо функціональну таблицю і визначаємо які сигнали потрібно подавати на входи не RS-тригерів для одержання необхідного результату.
Таблиця 9 – Функціональна таблиця
|
X |
t |
t+1 |
тригери |
|||||||||||||
|
Y1 |
Y2 |
Y3 |
Y4 |
Y1 |
Y2 |
Y3 |
Y4 |
YS1 |
YR1 |
YS2 |
YR2 |
YS3 |
YR3 |
YS4 |
YR4 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
~ |
1 |
~ |
1 |
~ |
0 |
1 |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
~ |
1 |
~ |
0 |
1 |
~ |
1 |
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
~ |
0 |
1 |
~ |
1 |
1 |
~ |
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
~ |
1 |
~ |
~ |
1 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
~ |
1 |
1 |
~ |
1 |
~ |
|
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
~ |
1 |
0 |
1 |
~ |
1 |
0 |
|
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
~ |
1 |
~ |
1 |
1 |
~ |
|
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
~ |
1 |
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
~ |
1 |
0 |
1 |
1 |
~ |
1 |
~ |
|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
~ |
1 |
1 |
~ |
1 |
~ |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
~ |
1 |
1 |
~ |
~ |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
~ |
1 |
1 |
~ |
1 |
0 |
~ |
1 |
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
~ |
1 |
1 |
~ |
1 |
~ |
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
~ |
1 |
0 |
|
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
~ |
1 |
1 |
0 |
~ |
1 |
1 |
~ |
|
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
~ |
0 |
1 |
1 |
~ |
1 |
~ |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
~ |
1 |
~ |
1 |
~ |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
~ |
1 |
~ |
~ |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
~ |
1 |
~ |
1 |
0 |
~ |
1 |
|
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
~ |
1 |
1 |
~ |
1 |
~ |
|
1 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
~ |
1 |
0 |
1 |
~ |
1 |
0 |
|
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
~ |
1 |
0 |
~ |
1 |
1 |
~ |
|
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
~ |
1 |
0 |
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
~ |
1 |
1 |
~ |
1 |
~ |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
~ |
1 |
1 |
~ |
0 |
1 |
~ |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
~ |
1 |
0 |
1 |
~ |
1 |
1 |
~ |
|
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
~ |
1 |
1 |
~ |
~ |
1 |
~ |
0 |
|
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
~ |
1 |
1 |
0 |
1 |
~ |
1 |
~ |
|
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
~ |
1 |
0 |
|
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
~ |
1 |
~ |
1 |
1 |
~ |
|
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
Будуємо карти Карно й одержуємо функції
для кожного входу кожного тригера.


![]()
![]()
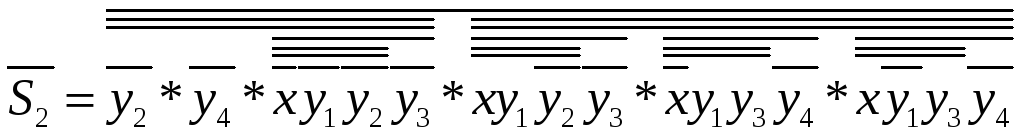
![]()

![]()
![]()
![]()
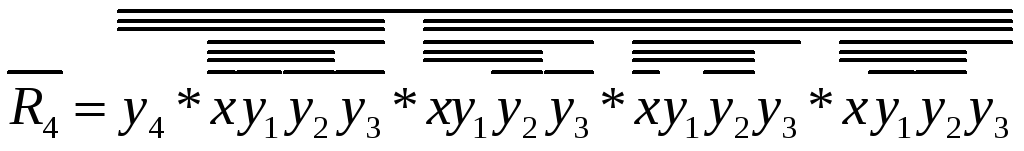
Схема реверсивного двійкового лічильника працюючого в коді Грея з М=12 наведена в доданку Ж.
