2 Автомати з пам’яттю
Автомати з пам’яттю характеризуються тим, що стан їх виходів залежить як від сигналів, присутніх на їх входах в даний момент часу, так і від послідовності сигналів, які надходили на входи автомата з пам‘яттю в попередній момент часу.
Для опису АП необхідно оперувати з двома різними функціями φ та f. Функція φ(функція переходів) описує зміну складу пам‘яті в залежності від того, що в ній зберігалося і від того, які зміни вхідних сигналів мали місце. Функція f(функція виходів) описує зміну вихідних сигналів АП під дією вхідних сигналів в залежності від того, що було записано в пам‘яті автомата.
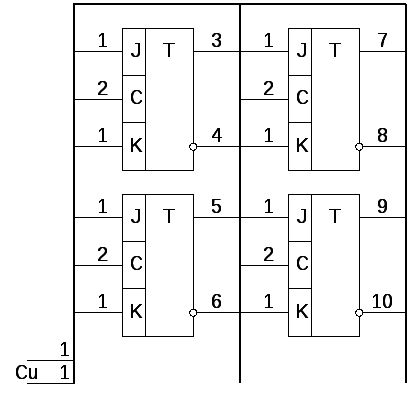
2.1 АП2-реверсивний 3-х розрядний регістр зсуву
Регістри зсуву – уявляє собою схему з зв’язаних між собою однобітових елементів пам’яті розташованих у єдиному корпусі.Регістри– це послідовність послідовно включених тригерів, яка призначена для зсуву сигналів, які подаються
на вхід регістру
і зберігання інформації.
Регістри зсуву діляться на:
-
з послідовним входом та послідовним виходом
-
з послідовним входом та паралельним виходом
-
з паралельним входом та послідовним виходом
Крім того регістр поділяється на регістр зсуву вправо, вліво та реверсивний( в залежності від управляючого сигналу регістр зсуву вліво сигнал який подається додається до молодшого розряду внутрішнього стану тригера, вправо – до старшого).
Етапи синтезу регістру зсуву
1. Словесне описання
-
Побудова графу переходів – виходів
-
Побудова функціональної таблиці
-
Побудова функціональної схеми регістру
Трьох розрядний регістр зсуву – це автомат другого роду, вихідні сигнали якого співпадають з його внутрішнім станом.
Спочатку
утворюється граф ,після побудови графа
будується функціональна таблиця.
Побудова функціональної таблиці автомата
приводиться наступним чином: так як
регістр зсуву 3-х розрядний, він має
формулу
=N;
23
=8 станів,
де N-
кількість
станів,
n- кількість
розрядів.
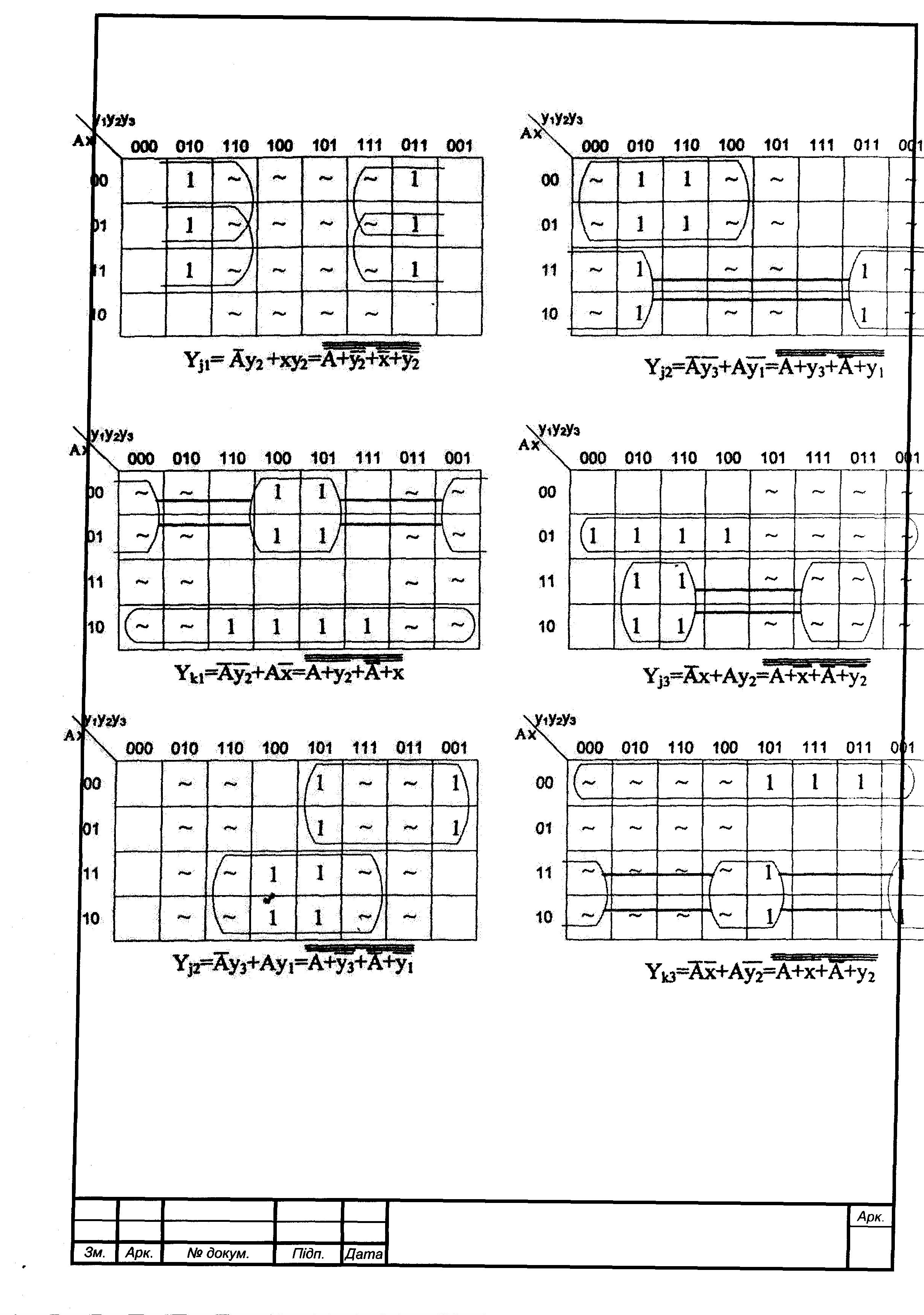
Функціональна таблиця дозволяє побудувати карти карно, для мінімізації входів тригера. За допомогою карт Карно визначається ФАЛ, які подаються на вході тригерів. Функцій 8 – стільки ж карт Карно.
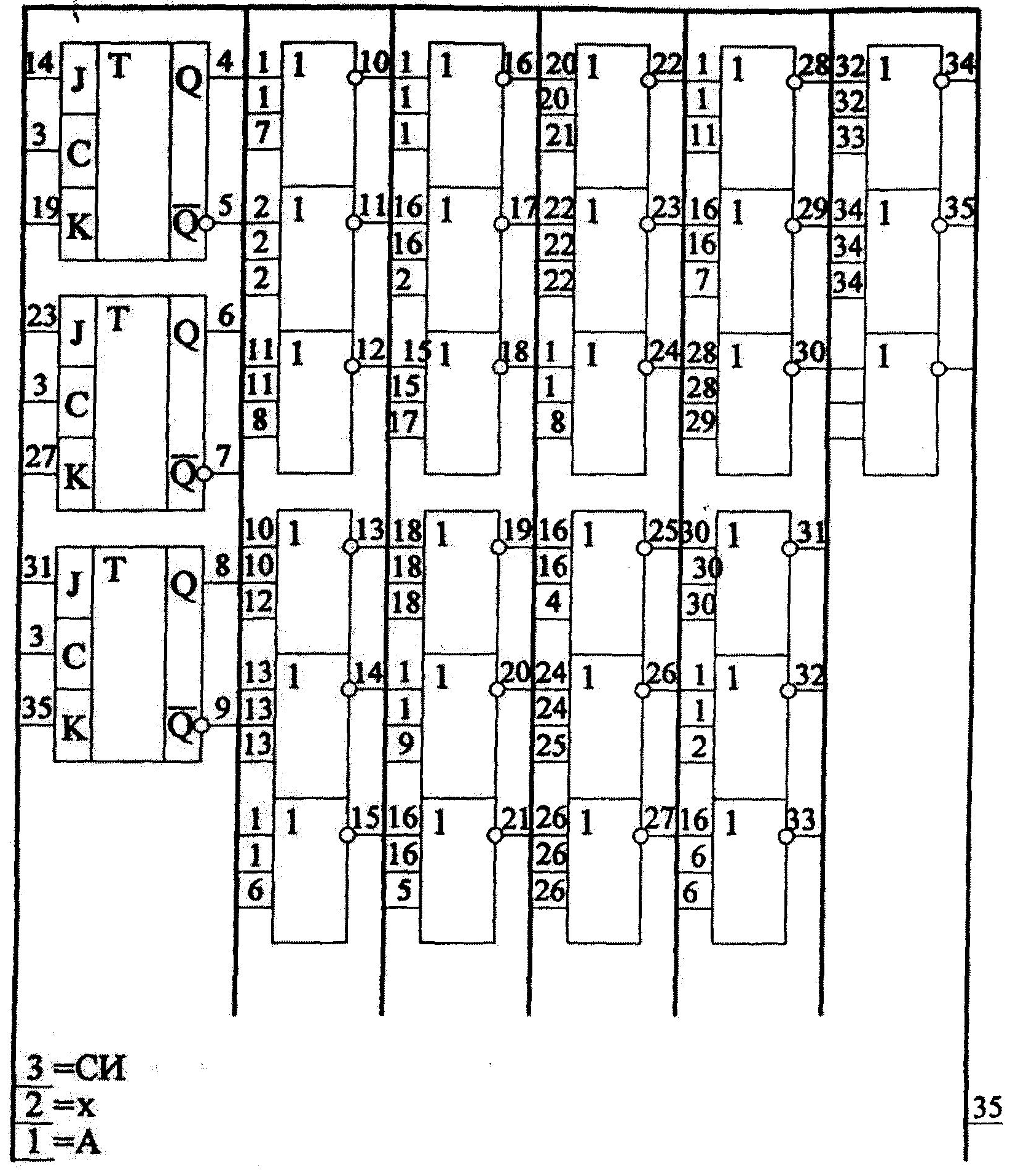
2.2 Двійковий обернений лічильник по модулю 15
Двійковий лічильник – це пристрій, який підраховує кількість імпульсів у вигляді двійкової інформації, які надходять на вхід. Кожному імпульсу, який надійшов на вхід відповідає відповідний код внутрішнього стану. Основним параметром лічильника є модуль рахунку, котрім називається максимальне число імпульсів, підраховуємих лічильником.
Види лічильників:
-
Прямого рахунку(сумуючі);
-
Зворотного рахунку(віднімаючі)
Також лічильники можуть бути реверсивними – в залежності від управляючого сигналу веде рахунок в прямому чи зворотному напрямі.
Спочатку утворюється граф ,після побудови графа будується функціональна таблиця. Функціональна таблиця дозволяє побудувати карти Карно, за допомогою яких визначається ФАЛ. Функцій 8 – стільки ж карт Карно. В шапку карти Карно входять 4 внутрішніх станів лічильника та управляючий сигнал.
t
t+1 Y1 Y2 Y3 Y4 Y1 Y2 Y3 Y4 Yj1 Yk1 Yj2 Yk2 Yj3 Yk3 Yj4 Yk4 0 0 0 0 1 1 1 1 1 ~ 1 ~ 1 ~ 1 ~ 0 0 0 1 1 1 1 0 1 ~ 1 ~ 1 ~ ~ 1 0 0 1 0 1 1 0 1 1 ~ 1 ~ ~ 1 1 ~ 0 0 1 1 1 1 0 0 1 ~ 1 1 ~ 1 ~ 1 0 1 0 0 1 0 1 1 1 ~ ~ 1 1 ~ 1 ~ 0 1 0 1 1 0 1 0 1 ~ ~ 1 1 ~ ~ 1 0 1 1 0 1 0 0 1 1 ~ ~ 1 ~ 1 1 ~ 0 1 1 1 1 0 0 0 1 ~ ~ ~ ~ 1 ~ 1 1 0 0 0 0 1 1 1 ~ 1 1 ~ 1 ~ 1 ~ 1 0 0 1 0 1 1 0 ~ 1 1 ~ 1 ~ ~ 1 1 0 1 0 0 1 0 1 ~ 1 1 ~ ~ 1 1 ~ 1 0 1 1 0 1 0 0 ~ 1 1 ~ ~ 1 ~ 1 1 1 0 0 0 0 1 1 ~ 1 ~ 1 1 ~ 1 ~ 1 1 0 1 0 0 1 0 ~ 1 ~ 1 1 ~ ~ 1 1 1 1 0 0 0 0 1 ~ 1 ~ 1 ~ 1 1 ~ 1 1 1 1 0 0 0 0 ~ 1 ~ 1 ~ 1 ~ 1
Yj1=1 Yj2=1
Yk2=1 Yk2=1
Yj3=1 Yj4=1
Yk3=1 Yk4=1
