Решение алгебраических и тригонометрических уравнений и неравенств

Функции. Преобразование математических выражений

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Башкирский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

posobie_Maple.pdf

Скачиваний:

Добавлен:

17.05.2015

Размер:

948.67 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 33

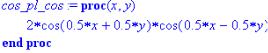
1	cos( x - y ) -	1	cos( x + y )
2		2

Но ни одна из встроенных функций не преобразует сумму тригонометрических функций в произведение. Этот пробел устраняется при помощи создаваемых пользователем по мере необходимости процедур. Например:

> combine(cos(x)+cos(y),trig,symbol); cos( x ) + cos( y )

>cos_pl_cos:=proc(x,y) 2*cos((x+y)*0.5)*cos((x-y)*0.5)

end;

>cos_pl_cos(x,3*x);

2 cos( 2 x ) cos( x )

Тригонометрические тождества, как и любые другие виды тождеств, доказываются при помощи встроенной функции testeq:

> testeq(cot(x)-tan(x)=2*cot(2*x)); true

Встроенная функция, предназначенная для решения уравнений и неравенств, имеет вид: solve(уравнение или неравенство, переменная)

> eqn:={b/(x-a)+a/(x-b)=2};

eqn := {	b	+	a	= 2 }
	x - a		x - b

> solve(eqn,x);

	{ x = b + a }, { x =			b	+	a	}
						2
		2
Пример:
> 3*log10(x^2)-(log10(-x))^2=9;
	3 ln( x2 )	-	ln( -x )2			= 9
	ln( 10 )		ln( 10 )2

>R0 := solve({3*ln(x^2)/ln(10)-ln(-x)^2/ln(10)^2 = 9});

R0 := { x = -1000 }, { x = -1000 }

Аналогично при помощиsolve решаются системы уравнений, только уравнения вводятся в виде множеств – в фигурных скобках. Пример:

> eqns:={2*x*y=1,x+z=0,2*x-3*z=2};

eqns := { 2 x y = 1, x + z = 0, 2 x - 3 z = 2 }

> solve(eqns,{x,y,z});

{ z =	-2		2		5
		, x =		, y =		}
	5		5		4

Проверим методом подстановки правильность решения системы: > subs(%,%%);

{ 0 = 0, 1 = 1, 2 = 2 }

Рассмотрим следующий пример. Пусть необходимо найти решение уравнения ln x - 2x(ln x -1) = 0

> eqn:=ln(x)-2*x*(ln(x)-1);

eqn := ln( x ) - 2 x ( ln( x ) - 1 )

Следует отметить, что выражение eqn можно не приравнивать нулевому значению, это по умолчанию будет сделано в команде solve:

> a:=solve(eqn,x);

a := e RootOf( -_Z + 2 _Z e_Z - 2 e_Z )

Если в выражении появилась функция RootOf, это означает, что Maple не может выразить корни в радикалах и решение выражается через корни аргумента этой функции. Если не указаны переменные, относительно которых должно быть найдено решение, то ответ будет выдан относительно всех переменных.

> evalf(%);

0.2800171480

Уравнения на максимум и минимум:

> eqns := max(x,3*x-12)=min(10*x+8,22-x);

eqns := max( x, -12 + 3 x ) = min( 10 x + 8, 22 - x )

> solve(eqns, {x});

{ x =	-8	}, { x =	17	}
	9		2

Для решения уравнений в численном виде служит командаfsolve (уравнение, переменная)

> a:=fsolve(eqn,x);

a := 3.258475747

В качестве следующего примера найдем корни полинома пятой

степени.

> pol:=205*x^5+140*x^4+70*x^2+5*x;

pol := 205 x5 + 140 x4 + 70 x2 + 5 x

Для обыкновенного линейного или нелинейного уравнения команда

f :=

9 - 8 x

fsolve найдет хотя бы одиночный реальный корень. Для полинома будут

вычислены все хорошо обусловленные корни, а исключительно плохо

Разностные уравнения или реккурентные соотношения:

обусловленные

могут

быть

пропущены. Для определения режима

> rsolve({f(n) = -3*f(n-1) - 2*f(n-2), f(1..2)=1},

нахождения корней используют следующие опции:

{f});

{ f( n ) = ( -2 )n - 3 ( -1 )n }

complex

- находит все комплексные корни

fulldigits

- опция, которая ограничивает команду fsolve от

выполнения

Для решения неравенств используется также команда solve.

промежуточных вычислений чисел высоких порядков. С этой

Пример: Решить неравенство log

2 x (x

- 5x + 6) < 1

опцией fsolve может решать плохо обусловленные задачи, но

> solve(log[2*x](x^2-5*x+6)<1,x);

решение занимает большее количество времени

1 ö

maxsols=n

- находит n

наименьших

корней. Эта

опция

применяется

RealRange ç Open( 0 ), Openç

÷, RealRange ( Open( 1 ), Open( 2 ) ),

только для полиномов, у которых более одного корня

2 ø

RealRange ( Open( 3 ), Open( 6 ) )

interval

- определяет интервал, в котором ведется поиск. Задается так:

В качестве

ответа

мы

получили3 интервала çæ0,

÷öÈ(1, 2

È) 3,(6 .

)

a..b или x=a..b или { x=a..b ,y=c..d,…}

> fsolve(pol,x,maxsols=3);

Выражение RealRange указывает на вещественную часть ответа, Open – на

-1., -0.07079255936, 0.

открытость границ интервала.

> fsolve(pol,x,-0.5..0);

Если

вы

хотите

получить

решение

неравенства

не

в виде

-0.07079255936, 0.

интервального множества типа xÎ(a, b), а в виде ограничений для искомой

Команда solve, примененная для решения тригонометрического

переменной типа a<x, x< b, то переменную, относительно которой следует

уравнения,

выдает

только

главные

решения, то

есть

решения

в интервале

разрешить неравенство, следует указывать в фигурных скобках. Например:

[0,2p]. Для

того, чтобы

получить

все

решения, следует предварительно

> solve(1-1/2*ln(x)>2,{x});

ввести

дополнительную

команду_EnvAllSolutions:=true.

{ 0 < x, x < e ( -2 ) }

Например:

Команда

rsolve(eq,f)

позволяет

решить

рекуррентное

> _EnvAllSolutions:=true: solve(sin(x)=cos(x),x);

p + p _Z1~

уравнение eq для целой функцииf. Можно задать некоторое начальное

условие для

функции f(n),

тогда

получиться

частное

решение

данного

В Maple символ _Z~ обозначает

константу

целого типа, поэтому

рекуррентного уравнения. Например:

решение данного

уравнения в

привычной

для нас

форме имеет вид

> eq:=2*f(n)=3*f(n-1)-f(n-2);

= p

/ 4

+ p

n , n Î Z .

eq := 2 f( n ) = 3 f( n - 1 ) - f( n - 2 )

x :

> rsolve({eq,f(1)=0,f(2)=1},f);

Универсальная команда solve позволяет решать функциональные

уравнения, например:

1 ön

> F:=solve(f(x)^2-3*f(x)+2*x,f);

-4 ç

F := proc(x) RootOf( _Z^2 - 3´_Z + 2´x ) end proc

Существует возможность находить только те решения уравнений,

В результате получается решение в неявном виде. Однако Maple

которые являются целыми. Это позволяет делать команда isolve(eqn, vars).

может работать с такими решениями. Неявное решение функционального

Например, если необходимо найти только целые значения параметраb, при

уравнения можно попытаться преобразовать в какую-либо элементарную

которых значение x=2 удовлетворяет неравенству

- x2

- 3

функцию с помощью командыconvert. Продолжая приведенный выше

b2 x2

+ x + 2

b2 x + b -1

пример, можно получить решение в явном виде:

> (x^3-x^2)/(b^2*x^2+x+2)<=(x^2-3)/(b^2*x+b-1);

> f:=convert(F(x),radical);

x3	- x2	£	x2 - 3
b2 x2 + x + 2			b2 x + b - 1

> subs(x=2,%);

4		£	1
4 b2
	+ 4 2 b2 + b - 1

> isolve(%,b);

{ b = 1 }, { b = -2 }

Лабораторная работа №1

В данном случае

уравнение4x3 - 2x4 = 0 , откуда

x4 = 2x 3 .

		- 1 -
	Разложить полином на множители
1)	p = x3 + 4x2 + 2x - 4	2)	p = x3 - 4x2 + 5x - 2

3)	p = x4 - 2x3 + x2	4)	p = 2x3 + x2 - 4x - 2
5)	p = x3 + 4x2 - 5x	6)	p = 5x4 + 9x3 - 2x2 - 4x -8

7)	p = x3 + 4x2 + 5x + 2	8)	p = 2x4 - 3x3 - 7x2 + 6x + 8

9)	p = x6 + 2x5 + 9x4 +16x3 +	10)	p = x6 + 3x5 + 7x4 + 9x3 +
9)	+ 24 x2 + 32x +16	10)	+ x2 - 3x -18
	+ 24 x2 + 32x +16		+ x2 - 3x -18
11)	p = x4 + 4x3 - 2x2 - 4x +1	12)	p = 2x3 - 5x2 -196x + 99

13)	p = 2x3 - x - 5x2 +1	14)	p = x3 - x2 - 8x +12

15)	p = x5 + 9x4 + 32x3 +	16)	p = 3x4 + 24x3	+ 70x2 +
	+ 57x2 + 51x +18		+ 87x + 38
17)	p = 2x3 +13x2 + 25x +14	18)	p = 8x3 + 42x2	+ 37x -12

19)	p = 3x4 - x3 + x2 + x - 4	20)	p = 8x3 - 36x2	+ 54x - 27

- 2 -

Определите функцию и при помощи операторов цикла for и while найдите последовательность ее значений на указанном

промежутке (протабулируйте)

1)	Записать функцию f ( x, y) =				x3 y2 - x	2 y3
							с помощью оператора
					( xy)5		с помощью оператора
					( xy)5
	присваивания и вычислите ее значения приy=1/a для x Î[-5a, 5a] с
	шагом a.
2)	Определите функцию f =			1 - x2 - y2		и перейдите в ней к полярным
	координатам x = r cos j ,			y = r sinj ; вычислите ее значения при r =1
	для j Î[p , 3p ] с шагом	p	.
	для j Î[p , 3p ] с шагом		.
	2

ìx, x < -1
ï	£ x < 1 и прибавьте к нейх.
3) Определите функцию f ( x) = í- x2 , -1	£ x < 1 и прибавьте к нейх.
ï- x, x ³ 1
î

Вычислите ее значения для x Î[-10, 10] с шагом 2.5.

4)	Определите	функцию	f (x) =	(		x4	)	значения для
							-1 / x . Вычислите ее
	x Î[-10, 10]	с шагом 2.	f (x) = (6x2				- x4 ) / 9 . Вычислите ее значения для
5)	Определите функцию
	x Î[-5, 5] с шагом 1.		f (x) = (x4 -10x2 + 9) . Вычислите
6)	Определите	функцию						ее значения
	для x Î[0, 5]	с шагом 0.5.		(
7)	Определите функцию		f (x) =		-x		2 + 3x -1 / x . Вычислите ее значения
							)

для x Î[-10, 10] с шагом 2.

8)Определите функцию f (x) = (x3 -1) / (x -1)3 . Вычислите ее значения

	для x Î[-10, 10] с шагом 2.5.
9)	Определите функцию	f (x) = x2 / (x - 2) . Вычислите ее	значения для
	x Î[-2, 6] с шагом 1.	f (x) = x / (x2 + 3x + 2) . Вычислите
10)	Определите функцию	f (x) = x / (x2 + 3x + 2) . Вычислите	ее значения

для x Î[-10, 10] с шагом 1.

11)Определите функцию f (x) = (x3 + 4) / (x +1)3 . Вычислите ее значения для x Î[-10, 10] с шагом 2.

12)Определите функцию f (x) = (x4 - 8) / (x +1)4 . Вычислите ее значения для x Î[-3, 3] с шагом 2.

13)	Определите	функцию	f (x) = 8 (x3 + x) / (2x +1)2 .					Вычислите	ее
	значения для x Î[-10, 10]		с шагом 2.
				x3		2
14)	Определите	функцию	f (x) =		- x		. Вычислите	ее значения	для
				6

x Î[-6, 6] с шагом 2.

15)

Определите

функцию

f (x) = arcsin ç

÷ . Вычислите

ее

значения

1+ x

для x Î[-1, 1]

с шагом 0.25.

16)

Определите

функцию

f (x) = sin4

x + cos4

x . Вычислите

ее

значения

для x Î[-2p , 2p ] с шагом

17)

Определите

функцию

+ 2, x

£1 . Вычислите

ее

значения

f (x) = í-x

î2x -1, x > 1

для x Î[-3, 3]

с шагом 1.

(

)

18)

Определите функцию

f (x) =

-x2

/ x . Вычислите ее значения

+ 3x -1

для x Î[-4, 4] с шагом 2.

19)

Определите

функцию f (x) = (x -1)2

(x - 2)3 / x . Вычислите

ее

значения для x Î[-3, 3]

с шагом 1.

20)

Определите функцию

f (x) = (x3 - 27)/ (x -1) . Вычислите ее значения

для x Î[-3, 3] с шагом 1.5.

- 2 -

Доказать тождество, преобразуя левую часть из суммы в произведение. Затем провести доказательство тождественности при

помощи встроенной функции testeq

1)cos x + cos 2x + cos 6x + cos 7x = 4 cos x cos 5x cos 4x

2 2

2)sin x - sin 2x + sin 3x = 4 cos 3x cos x sin x

3)sin x + 2 sin 3x + sin 5x = 4 cos2 x sin 3x

4)sin 2x + sin 4x - sin 6x = 4 sin x sin 2x sin 3x

5)sin x + sin 3x + sin 5x = tg3x

cos x + cos 3x + cos 5x

6)1- cos(2x -p ) - cos(4x +p ) + cos(6x - 2p) = 4 cos x cos 2x cos 3x

7)sin x + sin 5x = tg3x

cos x + cos 5x

8)1- sin 2x = ctg 2 æç p + x ö÷

è4 øsin 2x1 +

9)2 (cos x + sin x) = cos æç p - x ö÷ 2 è 4 ø

10)ctgx + tgx = 2ctg 2x

1+ tg 2xtgx

11)1- cos 2x + sin 2x = tgx

1+ cos 2x + sin 2x

12)	1+ sin 2x			-	1	- tg	2	x		= sin x
	1+ sin 2x				1	- tg		2
	sin x + cos x					+ tg	2	x
				1			2	x
				1				2
										æ p
		2								æ p	ö
13)			(cos x + sin x) = cos ç								- x ÷
13)	2		(cos x + sin x) = cos ç								- x ÷
	2								è 4		ø

14)cos 4x - sin 4xctg2x = cos 2x - 2 cos2 x

15)3 - 4 cos 2x + cos 4x = 8 sin4 x

16)cos 2x - cos 3x - cos 4x + cos 5x = -4 sin x sin x cos 7x

2 2


17)	sin 2x - sin 3x + sin 4x		= tg3x

	cos 2x - cos 3x + cos 4x
18)	sin2 4x			= 2 sin x sin 2x
	2 cos 2x + cos 3x + cos 5x

19)	(sin 2x - sin 6x)+ (cos 2x - cos 6x)				= 2 sin 2x

	sin 4x - cos 4x
20)	sin x + cos x	= tg3 x + tg 2 x + tgx +1

	cos3 x

Контрольные вопросы к лабораторной работе № 1

1.Что такое Maple и для чего он предназначен?

2.На какие условные части делится рабочее поле Maple и что в этих частях отображается? В каком режиме проходит сеанс работы в Maple?

3.Как перевести командную строку в текстовую и наоборот?

4.Какое стандартное расширение присваивается файлу рабочего листа

Maple?

5.Как получить приближенное значение рационального числа?

6.Какими разделительными знаками заканчиваются команды вMaple и чем они отличаются?

7.Какой командой осуществляется вызов библиотеки подпрограмм?

8.Опишите способы задания функций в Maple.

9.Какие операции Maple позволяет осуществлять с дробями?

10.В чем особенность работы встроенных функции при упрощении алгебраических выражений с рациональными степенями?

Глава 2

Геометрические построения на плоскости и в пространстве

Возможности геометрических построений вMaple огромны. Мы ограничимся только основными приемами построения и форматирования графиков.

Для построения двумерных графиков функцииf(x) одной переменной (в интервале a £ x £ b по оси Ох и в интервале c £ y £ d по оси Оу) используется команда plot(f(x), x=a..b, y=c..d, parameters), где parameters – параметры управления изображением. Если их не указывать, то будут использованы установки по умолчанию. Настройка изображения также может осуществляться с панели инструментов или при помощи всплывающего меню, которое вызывается нажатием правой кнопки мыши.

Основные параметры команды plot:

1)axes – установка типа координатных осей: axes=NORMAL – обычные оси; axes=BOXED – график в рамке со шкалой ; axes=FRAME – оси с центром в левом нижнем углу рисунка ; axes=NONE – без осей.

2)axesfont=[f,style,size] – установка параметров шрифта для осей (см. font).

3)сolor – установка цвета линии: английское название цвета, например, yellow – желтый и т.д.

4) coords=polar – установка	полярных	координат(по
умолчанию установлены декартовы).

5)discont=true – указание для построения выражений с разрывами.

6)font=[f,style,size] – установка типа шрифта для вывода текста: f задает название шрифтов: TIMES, COURIER, HELVETICA, SYMBOL; style задает стиль шрифта: BOLD, ITALIC, UNDERLINE; size – размер шрифта в pt.

7)labelfont=[f,style,size] – установка параметров шрифта для меток осей (см. font).

8)labels=[tx,ty] – надписи по осям координат: tx – по оси Оx и ty – по оси Оy.

9)linestyle=n – тип линии: непрерывная, пунктирная и т.д. (n=1

– непрерывная, установлено по умолчанию).

10)numpoints=n – число вычисляемых точек графика по оси абсцисс (по умолчанию n=49).

11) scaling	–	установка		масштаба	: рисунка
scaling=CONSTRAINED –			одинаковый	масштаб по	осям;
scaling=UNCONSTRAINED			– график	масштабируется	по
размерам окна.

12)style=line (point) – вывод линиями по умолчанию (построение по точкам, точки могут быть заданы парами в виде

списка é[x1, y1] , [x2, y2	] , ...,	[xn, yn]ù ).
ë		û

13)symbol=s – тип символа, которым помечают точки: BOX, CROSS, CIRCLE, POINT, DIAMOND.

14)thickness=n, где n=1,2,3… - толщина линии (по умолчанию n=1).

15)title=”text”, где text - заголовок рисунка (текст можно оставлять без кавычек, если он содержит только латинские буквы без пробелов).

16)titlefont=[f,style,size] – шрифт для заголовка.

17) xtickmarks=nx и ytickmarks=ny – число меток по осиОx

и оси Оy, соответственно.

С помощью команды plot можно строить помимо графиков функций y=f(x), заданной явно, также графики функций, заданных параметрически y=y(t), x=x(t), если записать команду

plot([y=y(t), x=x(t), t=a..b], parameters).

Рассмотрим некоторые примеры.

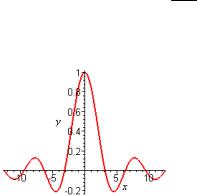
Пример 1. Пусть необходимо построить график y = sin x жирной линией в x

интервале от -4p до 4p.

> plot(sin(x)/x, x=-4*Pi..4*Pi, labels=[x,y], labelfont=[TIMES,ITALIC,12], thickness=2);

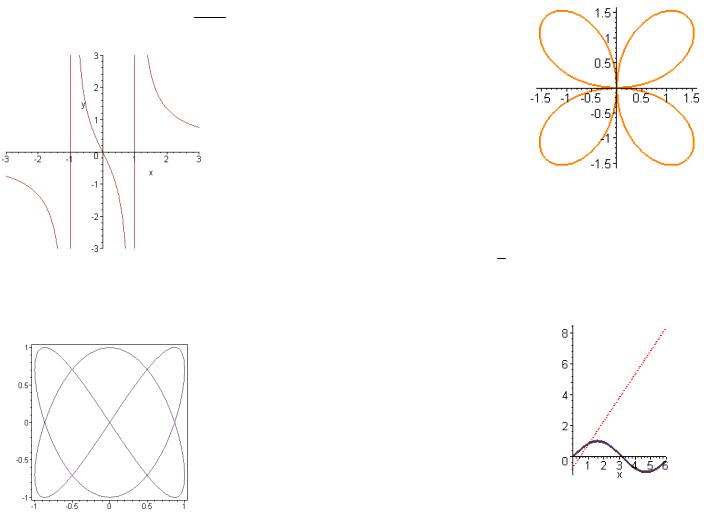
Пример 2. Построить график разрывной функции y = 2x . x 2 -1

> plot(2*x/(x^2-1),x=-3..3,y=-3..3,color=brown);

Пример 3. Построить

график

параметрической

кривойy = sin 2t ,

x = cos3t , 0 £ t £ 2p в рамке.

> plot([sin(2*t),cos(3*t),t=0..2*Pi], axes=BOXED, color=violet);

Пример 4. Построить в полярной системе координат график функции

r= 2 sin 2t

>plot(2*sin(2*t), t=0..2*Pi, coords=polar, color=coral, thickness=2);

Одновременно можно строить графики нескольких функций.

Пример 5. Пусть необходимо построить на одном рисунке графики функций

y = sin(x) и y = 3 x - ln 2 . 2

> plot([sin(x), 3*x/2-ln(2)], x=0..6, scaling=

CONSTRAINED, color=[violet,red], linestyle=[1,2], thickness=[3,2]);

Точки таблично заданной функции строятся так ,жекак график функции, заданной параметрическими уравнениями, но с заданием дополнительных параметров: style=point, symbol=box.

Пример 6. Построить точки таблично заданной функции

x	1	2	3	4	5
y	-2	5	-1	3	4.5

> x:= vector([1,2,3,4,5]): y:=vector([-2,5,-1,3,4.5]): plot( [x[i],y[i], i=1..5], x=0..5, y=-10..10, style= point, symbol=box);

Для построения областей плоскости, соответствующих заданным неравенствам, используется команда inequal из пакета plots. В команде inequals({f1(x,y)>c1,…,fn(x,y)>cn},x=x1..x2,y=y1..y2, options) в фигурных скобках указывается система неравенств, определяющих область, затем размеры координатных осей и параметры. Параметры регулируют цвета открытых и закрытых границ, цвета внешней и внутренней областей, а также толщину линий границ:

- optionsfeasible=(color=red) – установка цвета внутренней области;

–optionsexcluded=(color=yellow) – установка цвета внешней области;

–optionsopen(color=blue, thickness=2) – установка цвета и толщины линии открытой границы;

–optionsclosed(color=green,thickness=3) – установка цвета и толщины линии закрытой границы.

Пример 7. Построить замкнутую область, ограниченную неравенствами

x+y £ 1 , x ³ 0 , y ³ 0

> with(plots): inequal({x+y<=1, x>=0, y>=0}, x= -1..2, y=-

1..2,optionsfeasible=(color=red),optionsopen= (color = blue,thickness=2), optionsclosed=(color=green, thickness=3), optionsexcluded=(color=yellow),labels=[x,y]);

Если функция задана неявно уравнениемF (x, y) = 0 , то для построения ее графика используется командаimplicitplot из графического пакета plots: implicitplot(F(x,y)=0, x=x1..x2, y=y1..y2).

> with(plots): implicitplot( x^2/4-y^2/2=16, x=-

20..20, y=-16..16, color=green, thickness=2);


Теперь		коротко осветим некоторые возможности трехмерной
графики (3D-графики).			График функции z = f ( x, y) можно нарисовать,
используя	команду		plot3d(f(x,y),	x=x1…x2,	y=y1…y2,
options). Параметры этой команды частично совпадают с параметрами
команды	plot. К	часто используемым		параметрам	командыplot3d

относится light=[angl1, angl2, c1, c2, c3] – задание подсветки поверхности, создаваемой источником света из точки со сферическими координатами (angl1, angl2). Цвет определяется долями красного(c1), зеленого (c2) и синего (c3) цветов, которые находятся в интервале[0,1]. Параметр style=opt задает стиль рисунка: POINT –точки, LINE – линии, HIDDEN – сетка с удалением невидимых линий, PATCH – заполнитель (установлен по умолчанию), WIREFRAME – сетка с выводом невидимых линий, CONTOUR – линии уровня, PATCHCONTOUR – заполнитель и линии уровня. Параметр shading=opt задает функцию интенсивности заполнителя, его значение равно xyz – по умолчанию, NONE

– без раскраски.

Если требуется построить поверхность, заданную параметрически: x=x(u,v), y=y(u,v), z=z(u,v), то эти функции перечисляются в квадратных

скобках	в	команде: plot3d([x(u,v),			y(u,v),	z(u,v)],
u=u1..u2, v=v1..v2).
Трехмерный график			поверхности, заданной неявно			уравнением
x Î [-10,	10 ] ,	строится	с	помощью	команды	пакетаplot:
				30

implicitplot3d(F(x,y,z)=c, x=x1..x2, y=y1..y2, z=z1..z2), где указывается уравнение поверхностиx Î [- 5 , 5 ] и размеры рисунка по координатным осям.

> with(plots): implicitplot3d(x^2+y^2+z^2=4, x=-2..2, y=-2..2, z=-2..2, scaling=CONSTRAINED);

В пакете plot		имеется команда spacecurve				для построения
пространственной			кривой,	заданной		параметрически:
x = x(t), y = y(t), z = z(t) .				Параметры			: команды
spacecurve([x(t),y(t),z(t)],t=t1..t2), где						переменная t
изменяется от t1 до t2.
Часто бывает необходимо совместить на одном рисунке несколько
графических	объектов, полученных			при	помощи	различных	команд,
например, добавить к графику, нарисованному командой plot, текстовые
надписи, полученные командой. Для этого результат действия команды
присваивается некоторой переменной:
> p:=plot(…): t:=textplot(…):
При	этом	на	экран	вывод не производится. Для			вывода
графических	изображений		необходимо		выполнить	команду	из пакета
plots:

> with(plots): display([p,t], options).

Лабораторная работа №2

Графика Maple . Решение алгебраических и тригонометрических уравнений и неравенств

- 1 –

Построение графиков функций

1)Построить на отдельных рисунках графики функций Бесселя первого рода Jn(x) для различных ее номеровn в интервале–20<x<20. Функции Бесселя вызываются командойBesselJ(n,x), где n – номер функции Бесселя, x – независимая переменная. Построить первые 4 функций Бесселя дляn=0,1,2,3. Сделать подписи осей курсивом.

2)Построить на отдельных рисунках графики функций Бесселя второго

рода Yn(x) для различных ее номеровn в интервале 0<x<20. Функции

Бесселя вызываются командойBesselY(n,x),

где

– номер

функции Бесселя, x – независимая переменная. Построить

первые 5

функций Бесселя.

Сделать

заголовок

рисунка“Функций

Бесселя

второго рода” жирным шрифтом.

sin nx

Построить

на

отдельных

рисунках

графики

функций

для

различных ее номеров n=10, 15, 20, 25 в интервале -p <x< p . Выбрать

пунктирный тип линии.

tg nx

Построить

на

отдельных

рисунках

графики

функций

для

номеров n

интервале0<x< p

для n=5,

различных

ее

10, 15,

20.

Установить оси с центром в левом нижнем углу рисунка.

Построить

на

отдельных

рисунках

графики

функций

для

ln nx

различных ее номеров n в интервале 0<x< p , 0<y<5 для n=2, 5, 7, 9.

Сделать заголовок рисунка.

функцийy = tg x

+ ctg x ,

Построить

на

одном

рисунке

графики

y = 2cos3x ,

y = х2 + sin x

различными цветами и промасштабировать

последний график

по размерам окна. Сделать подписи осей жирным

шрифтом.

y = 2-x ,

Построить

на

одном

рисунке

графики

функцийy= 4-x2 ,

y =

-4

учитывая их области определения;

установить толщину линии

2, 3, 4 соответственно. Сделать заголовки рисунков курсивом.

Построить

на

одном

рисунке

графики

функцийy =

- sin10x ,

y = 2x sin x - cos x ,

y = x2

- 5x

интервале -2p £ x £ 2p , установив

толщину линий 1, 3, 5 соответственно. Задать 10 меток по оси Оx и 8

меток по оси Оy.

Построить

на

одном

рисунке графики

функцийy=1-

2cos2x

y = x +1 -

3 - x ,

y = 4 -

учитывая

их области

определения.

Установить

следующие

параметры

шрифта

для

меток :

осей10,

COURIER, ITALIC.

10) Построить

на

одном

рисунке

графики

функциy = йx + 2 ,

y = - x 16 - x2 , y = x6 -1 учитывая их области определения. Сделать

подписи осей курсивом.

Построить график функции в полярных координатах (11-20)

11)	r = cos3 (j/ 3)	при 0<j<4p. Используйте цвет линии под		названием
	magenta, установите толщину линии 3.
12)	r = aj (архимедова спираль). Используйте цвет линии под названием
	violet, установите толщину линии 2.
13)	r = a(1 - cos j)	при	-4p<j<4p. Используйте цвет	линии под
	названием gold, установите толщину линии 4.
14)	r = a 2 cos 2j (лемниската). Сделать заголовок рисунка “Лемниската”
	жирным шрифтом.

15)r = a (гиперболическая спираль), сделать подписи осей курсивом. j

16)r = a(1 + 2 cos j) , сделать заголовок рисунка “Улитка Паскаля”.

17)	r = 2a sin j ,		вынести	название	получившейся	фигуры в	заголовок,
	линию вывести желтым цветом.
18)	r = ej , установите			толщину	линии3, сделать заголовок		рисунка
	“логарифмическая спираль”.
19)	r =	2a	, цвет линии coral, толщина линии			2.
19)	r =	1 + cos j	, цвет линии coral, толщина линии			2.
		1 + cos j
20)	r = 1 + cosj ,		установить подпись “кардиоида”,			цвет линии	выбрать

зеленым.

21)Построить на одном рисунке графики функцииy = x + 2arcctgx и ее асимптот y = x и y = x + 2p . Установить следующие параметры: цвет

основной линии – голубой, асимптот – красный (установлен по умолчанию, поэтому его можно не изменять); толщина основной линии

– 3, асимптоты – обычной; масштаб по координатным осям– одинаковый. Сделать надписи: какая функция относится к какой линии. Указание: использовать для преобразования в текст формул

команду convert, а для построения графиков и надписей команды textplot и display из пакета plots.

22) Нарисовать параметрически заданную поверхность(лист Мебиуса):


æ		æ v	öö
x = ç5	+ u cosç		÷÷cos v

ç		è 2	÷
è			øø
v Î[0,2p] ,		u Î[-1,1] .
0<v<2p,		-1<u<1,

	æ	æ v	öö		æ v		ö
,	y = ç5	+ u cosç	÷÷sinv ,	z = u sinç			÷ ,

	ç	è 2	÷		è 2		ø
	è		øø
Задайте изменение			координат	в	интервалах
и	установите		следующие			параметры:

grid=[60,10], orientation=[-106,70], axes=FRAMED,

tickmarks=[5,8,3].

Также

выведите

название

рисунка,

подпишите названия осей и установите одинаковый масштаб по осям.

23)

Построить

на

одном

рисунке

графики

астроидыx = 4cos3 t ,

x = 2 sin3 t

( 0 £ t £ 2p ) вписанной

эллипс

y 2

= 1 .

Выведите

название

линий Astroida

и Ellips

жирным шрифтом

вместе с

его

уравнением курсивом.

x + y > 0 ,

x - y £ 1 ,

24)

Построить

область, ограниченную

линиями:

y = 2 .

25)

Выполнить

построение

двух поверхностейz = x sin 2 y + y cos 3x

z = x2 + y 2 - 7

в пределах ( x, y) Î[ -p, p] . Установите переменный

цвет поверхностей как функцию x + y .

0, 2

26)

Построить

поверхность

z =

x2 + y2

(x +1, 2)2

+ ( y -1, 5)2

0, 3

вместе с линиями уровня.

(x - 0, 9)2

+ ( y +1,1)2

27)Построить примерную форму электронного облака атома. Форма электронного облака определяется двумя квантовыми числами: число l

– определяет тип орбитали, число m – определяет магнитный момент электрона. При m=0 форма электронного облака задается полиномами

Лежандра первого рода: P( x) =		1	d n	( x2 -1)n	. Следует построить
Лежандра первого рода: P( x) =				( x2 -1)n	. Следует построить
		2n n! dxn
параметрически	заданную	поверхность: x(q,j) = Y (j)sin jcos q ,
y(q,j) = Y (j)sin jsin q,		z(q,j) = Y (j)cos j ,				где
Y (j) = 2l +1 P(cos j) . Вначале положите l=3.
4p
		34

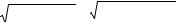
28) Построить пространственную кривую: x = sin t , y = cos t , z = et . Сделать подписи осей курсивом.

- 2 -

Решение уравнений, систем и неравенств

1)Найти все решения системы уравнений ïíx2 - y 2 = 1,

ïx2 + xy = 2.

îì

2) Найдите

функцию f(x),

удовлетворяющую

уравнению

f2 ( x) - 2 f ( x) = x .

3)Найдите все решения уравнения 5sin x + 12cos x = 13 .

4)Решите неравенство 13x3 - 25x2 - x4 -129x + 270 > 0 . Запишите этот результат в аналитическом виде. Получите решение этого неравенства

ввиде ограничений для искомой переменной.

5)	Решите неравенство e(2x +3) < 1 . Получите решение этого неравенства
	в виде ограничений для искомой переменной.
					ì	2	- 5xy + 6 y	2	= 0,
6)	Найти	все	точные	решения	ïx		- 5xy + 6 y		= 0,
6)	Найти	все	точные	решения	системы				в
					í	2 + y2 =10
					ïx	2 + y2 =10
					î
	аналитическом виде.
7)	Найти		все	решения	тригонометрического					уравнения

sin4 x - cos4 x = 1 / 2 .

Найти

численное

решение

= 2(1 - x)

Решить

уравненияe

неравенство 2 ln2 x - ln x < 1 .

Найти

решение

уравнения

x + (x +1)

= 2

аналитическом и

численном виде.

x + ex > 0 в аналитическом и численном

10)

Найти решение уравнения

виде.

11)

Найти решение уравнения

2 arcsin x - arccos 3x = 0 в аналитическом и

численном виде.

12)

Решите

неравенство (x - 3)(2 - x) <

4x 2 +12x +11 .

Запишите этот

результат в аналитическом виде.

13)

При

всех

значениях

a (a > 0, a ¹ 1)

решить

неравенство

a2 x + ax +2 -1

³ 1.

Получить

решение этого неравенства в виде

ограничений для искомой переменной.

x + x

14)

Решите неравенство log1

çlog6

< 0 .

x + 4

æ 3 öx -1

4 53x -4

15)

Найти решение уравнения

5 ø

16)

ì3x + 7 y = 20

Найти все решения параметра a , при которых система í

îax +14 y = 15

имеет единственное решение.

17)

Найти

все пары целых чиселx

y ,

удовлетворяющие

условию

x + y = xy .

ì2x - 3y + 5z + 7t =1,

18)

Найти общее и одно частное решение системы: íï4x - 6 y + 2z + 3t = 2,

î2x - 3y -11z -15t =1.

ì2x - 3y = 6,

19)

Пересекаются ли в одной точке прямые íï3x + y = 9, и íïx + 2 y = 4, ?

+ 4 y = 3

= 5

îx

îx -5 y

20)

При

каких

значениях

параметраl

система

имеет

решение

ìla + 2b = 3,

î8a + 4lb = 9

Контрольные вопросы к лабораторной работе № 2

1. С помощью каких команд строятся графики на плоскости и в пространстве? Какие аргументы имеют эти команды?

2.Как называется пакет дополнительных графических команд?

3.С помощью какой команды можно построить график неявной функции? Опишите ее параметры.

4.Для чего предназначена команда display?

5.Какая команда позволяет построить двумерную область, заданную системой неравенств?

6.С помощью какой команды можно построить график пространственной кривой?

7.Для чего предназначена команда solve?

8.Какие команды используются для численного решения уравнений и для решения рекуррентных уравнений?

9. Какие дополнительные команды	следует ввести для , тогочтобы
получить точное решение уравнения,	все решения уравнения?

10.В каком виде выдается решение неравенства? Как отличить в строке вывода закрытый интервал от открытого?

Глава 3

Элементы математического анализа

Для вычисления пределов имеются две команды:

1)прямого исполнения – limit(expr,x=a,par), где expr –

выражение, предел которого следует найти, a – значение точки, для которой вычисляется предел, par – необязательный параметр для поиска односторонних пределов (left – слева, right – справа) или указание типа переменной (real – действительная, complex – комплексная).

2)отложенного исполнения – Limit(expr,x=a,par), где параметры команды такие же, как и в предыдущем случае.

Приведем пример, который проиллюстрирует удобное применение этих команд для аналитических выкладок:

>Limit(1/(1+exp(1/x)),x=0,left)=limit(1/(1+exp(1/x)),

x=0,left);

lim	1		= 1
	æ 1	ö
x ® 0-	ç	÷

	ç	÷
	1 + eè x	ø

Для вычисления производных в Maple имеются две команды:

1)прямого исполнения – diff(f,x), где f – функция, которую следует продифференцировать, x – имя переменной, по которой производится дифференцирование.

2)отложенного исполнения – Diff(f,x), где параметры команды такие

же, как и в предыдущей. Действие этой команды сводится к аналитической


записи	производной в		виде	¶	f ( x) .	Для вычисления	производных

				¶x		параметрахx$n, где n – порядок
старших	порядков следует		указать в
производной		После	выполнения			дифференцирования		полученное
выражение желательно упростить. Для этого следует использовать команды
simplify,		factor или expand, в зависимости от того,					в каком виде

вам нужен результат. Пример:

> Diff(cos(2*x)^2,x$4)=diff(cos(2*x)^2,x$4);

d4 ( cos( 2 x )2 ) = -128 sin( 2 x )2 + 128 cos( 2 x )2 dx4

Полученное выражение можно упростить двумя способами: > simplify(%);

	d4			( cos ( 2 x )2 ) = 256 cos( 2 x )2 - 128
	dx4			( cos ( 2 x )2 ) = 256 cos( 2 x )2 - 128
	dx4
> combine(%%);
		d4		æ1	cos( 4 x ) +	1	ö	= 128 cos( 4 x )
				ç			÷
			4	ç			÷
		dx		è2		2	ø

Для определения дифференциального оператора используется команда D(f) – f-функция, например:

> D(cos);

-sin

Вычисление производной в точке: > D(sin)(Pi):eval(%);

-1

Оператор дифференцирования применяется к функциональным операторам

> f:=x-> sin(x^3)+exp(3*x):D(f);

x ® 3 cos( x3 ) x2 + 3 e ( 3 x )

Рассмотрим пример. Вычислить вторую производную функции

y= sin2 x /(2 + sin x) в точках x=p/2, x=p.

>y:=sin(x)^2/(2+sin(x)): d2:=diff(y,x$2):

>x:=Pi; d2y(x)=d2;

x:= p

d2y( p) = 1

> x:=Pi/2;d2y(x)=d2;

x :=

d2yæçè p2 ö÷ø = -95

Для вычисления частных производных функцииf (x1 ,..., xN )

также используется команда diff. В этом случае эта команда имеет такой формат: diff(f,x1$n1,x2$n2,…, xm$nm), где x1,…, xm –

переменные, по которым производится дифференцирование, а после знака $ указаны соответствующие порядки дифференцирования. Например: найти

¶f	и	¶f	функции f = arctg	x	.
¶x		¶y
				y

> f:=arctan(x/y): Diff(f,x)=simplify(diff(f,x));

¶	arctan	x	=	y
¶x				x2 + y2
		y

> Diff(f,y)=simplify(diff(f,y));

¶	arctan	x	= -	x	.
¶y				x2 + y2
		y

Займемся исследованием функции. Исследование функции необходимо начинать с нахождения ее области определения, но это трудно автоматизируемая операция, при рассмотрении этого вопроса приходится решать неравенства. Ответить на вопрос, определена ли функция на всей числовой оси, или нет, можно исследовав ее на непрерывность.

Непрерывность функции и точки разрыва

Проверить непрерывность функции f(x) на заданном промежутке [x1,x2] можно с помощью команды iscont(f,x=x1..x2). Если функция f непрерывна на этом интервале, то в поле вывода появится ответtrue – (истина); если функция f не является непрерывной на этом интервале, то в поле вывода появится ответfalse – (ложь). В частности, если задать интервал x=-infinity..+infinity, то функция f будет проверяться на всей числовой оси. В этом случае, если будет получен ответtrue, то

можно сказать, что функция определена и непрерывна на всей числовой оси. В противном случае следует искать точки разрыва. Это можно сделать двумя способами:

1)с помощью команды discont(f,x), где f – функция, исследуемая на непрерывность, x – переменная. Эта команда используется для нахождения точек разрыва первого и второго родов.

2)с помощью командыsingular(f,x), где f – функция, x –

переменная. Эта команда используется для нахождения точек разрыва второго рода как для вещественных значений переменной, так и для

комплексных.
Перед использованием этих команд их следует	обязательно
загрузить из стандартной библиотекиreadlib(name), где name	– имя

любой из указанных выше команд.

Обе эти команды выдают результаты в виде перечисления точек разрыва в

фигурных скобках. Тип	такой	записи называетсяset. Для того, чтобы в
дальнейшем можно	было	использовать полученные значения точек

разрыва, следует из типа set с помощью команды convert перевести их в обычный числовой тип.

> readlib(iscont):

> iscont(exp(1/(x+3)),x=-infinity..+infinity); false

>readlib(discont):discont(exp(1/(x+3)),x);

{-3 }

Экстремумы. Наибольшее и наименьшее значение функции

Для исследования функции нескольких переменных на экстремум в Maple имеется команда extrema(f,{cond},x,’s’) , где f - функция, экстремумы которой ищутся, в фигурных скобках{cond} указываются ограничения для переменной, х – имя переменной, по которой ищется экстремум, в апострофах ’s’ – указывается имя переменной, которой будет присвоена координата точки экстремума. Если оставить пустыми фигурные скобки {}, то поиск экстремумов будет производиться на всей числовой оси. Результат действия этой команды относится к типуset. Пример:

>extrema(x^3+3*x*y^2-15*x-12*y,{},{x,y});

{-28, 28 }

>solve({diff(x^3+3*x*y^2-15*x- 12*y,x)=0, diff(x^3+ 3*x*y^2-15*x-12*y,y)=0, x^3+3*x*y^2-15*x-12*y=-28});

{y = 1, x = 2 }

>solve({diff(x^3+3*x*y^2-15*x-12*y,x)=0, diff(x^3+ 3*x*y^2-15*x-12*y,y)=0, x^3+3*x*y^2-15*x-12*y=28});

{y = -1, x = -2 }

Задачи на условный экстремум решаются этой же встроенной функцией с указанием в качестве{cond} ограничений на переменные. Например, пусть необходимо найти условные экстремумы функции u = xyz

при x + y + z = 4 , xy + yz + zx = 5 .

> extrema(x*y*z,{x+y+z=4,x*y+y*z+z*x=5},{x,y,z});

50 { 2, 27 }

> solve({x*y*z=2,x+y+z=4,x*y+y*z+z*x=5},{x,y,z});

{ x = 1, y = 2, z = 1 }, { y = 1, x = 2, z = 1 }, { x = 1, y = 1, z = 2 }

> solve({x*y*z=50/27,x+y+z=4,x*y+y*z+z*x=5},{x,y,z});

{ x =	5	, z =		5	, y =	2	}, { z =	2	, y =		5	, x =	5	}, { y =	5	, z =	5	, x =		2	}
	3			3		3		3			3		3		3		3		3

Команда			extrema				не дает			ответ на				вопрос ,		какая из			точек

экстремума есть максимум, а какая – минимум. Наибольшее и наименьшее

значение

функции f(x) на

заданном

промежутке[a, b] находятся

встроенными функциями maximize(f,x=a..b) и minimize(f,x= a..b) соответственно. Если требуется получить и координаты точки, в которой принимается такое значение, то в список параметров необходимо добавить location или location = true. Пример:

> minimize(x^4 - x^2, x=-3..3, location=true);

-1

{ x = -

-1 ù é

{ x =

-1

, { ê

2 },

ú, ê

}

Необходимо

отметить,

что команды extrema,

maximize

minimize

обязательно

должны

быть

загружены

из

стандартной

библиотеки

командой readlib(name),

где

name –

имя

загружаемой

команды.

Рассмотрим еще один пример: найти условные

экстремумы

функции f(х,у)=xy+yz при x2+y2=2, y+z=2, x>0, y>0, z>0.

> restart: readlib(extrema): f:=x*y+y*z:

assume(x>0);assume(y>0);assume(z>0);

simplify(extrema(f,{x^2+y^2=2,y+z=2},{x,y,z}, 's'));

RootOf( _Z

+ 4 _Z + 1, label

_L1 )

{ minç

, 0

÷,

RootOf( _Z

+ 4 _Z + 1, label = _L1 ) +

maxç

, 2

÷}

> convert(%,radical); convert(s,radical);

3 3

, 2

, 0

{ maxç

÷, minç

÷}

{{x~=1,z~=1,y~=1},{x~=-1,z~=1,y~=1},

{x~= - 1 - 1 3 ,y~= - 1 (-2 +

3)(1 +

3) , z~= 5 - 1

3 }}

В этом случае командаextrema

сама

определила

характер

экстремумов, однако, в каких точках функция имеет экстремумы, можно

определить подстановкой.

Исследование функции по общей схеме

1. Область

определения

функцииf(x)

–

полностью

может

быть

указана после исследования функции на непрерывность.

2. Непрерывность и точки разрыва функции f(x) исследуются по схеме:

>iscont(f, x=-infinity..infinity);

>d1:=discont(f,x);

>d2:=singular(f,x);

Врезультате наборам переменным d1и d2 будут присвоены значения x-координат в точках разрыва 1 и 2-го рода (если они будут найдены).

3. Асимптоты. Точки бесконечных разрывов определяют вертикальные асимптоты графика f(x). Уравнение вертикальной асимптоты

имеет вид: > yr:=d2;

Поведение функции f(x) на бесконечности характеризуется наклонными асимптотами (если они есть). Уравнение наклонной асимптоты y=kx+b, где коэффициенты вычисляются по формулам:

k = lim	f ( x)	и b = lim ( f ( x) - kx) .

x ®+¥ x		x ®+¥
Аналогичные формулы		для x ® -¥ . Поэтому нахождение

наклонных асимптот можно провести по следующей схеме:

>k1:=limit(f(x)/x, x=+infinity);

>b1:=limit(f(x)-k1*x, x=+infinity);

>k2:=limit(f(x)/x, x=-infinity);

>b2:=limit(f(x)-k2*x, x=-infinity);

Часто оказывается, что k1=k2 и b1=b2, в этом случае будет одна асимптота при x ® +¥ и при x ® -¥ . С учетом этого составляется уравнение асимптоты

>yn:=k1*x+b1;

4.Экстремумы. Исследование функции f(x) на экстремумы можно проводить по схеме:

>extrema(f(x), {}, x, ’s’);

>s;

>fmax:=maximize(f(x), x);

>fmin:=minimize(f(x), x);

После выполнения этих команд будут найдены координаты(x, y) всех максимумов и минимумов функции f(x).

5. Построение графика функцииf(x) – это окончательный этап исследования функции. На рисунке помимо графика исследуемой функции f(x) должны быть нанесены все ее асимптоты пунктирными линиями, подписаны координаты точек max и min.

Аналитическое и численное интегрирование

Для	нахождения	неопределенного	ò
			интегралаf ( x)dx
		44

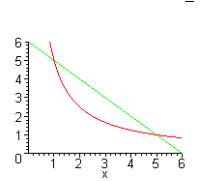
используется 2 команды:

1)прямого исполнения – int(f, x), где f – подынтегральная функция,

x– переменная интегрирования;

2)отложенного исполнения – Int(f, x) – где параметры команды такие же, как и в команде прямого исполненияint. Команда Int выдает на экран интеграл в аналитическом виде математической формулы.

Для вычисления определенного интеграла в командах int и Int добавляются пределы интегрирования.

Рассмотрим решение одной из типичных задач на интегрирование:

Найти площадь фигуры, ограниченной линиями y = 5 и y = 6 - x . x

> plot([5/x,6-x],x=0..6,0..6);

Найдем абсциссы точек пересечения графиков функций, вычислим площадь и оценим результат:

> solve(5/x=6-x,x);

5, 1

> int(6-x-5/x,x=1..5);

-5 ln( 5 ) + 12

> evalf(%);

3.952810440

Добавление опции continuous дает возможность Maple игнорировать любые возможные разрывы подынтегральной функции в диапазоне интегрирования. Это позволяет вычислять несобственные интегралы от неограниченных функций. Несобственные интегралы с бесконечными пределами интегрирования вычисляются, если в параметрах команды int указывать, например, x=0..+infinity.

Пример:	вычислить несобственный интеграл или установить его
¥	1 + 2x
расходимость ò				dx .
расходимость ò	x	2	(1+ x)	dx .
1	x		(1+ x)
				45

> int( (1+2*x)/((1+x)*x^2),x=1..infinity); ln( 2 ) + 1

> evalf(%,3);

1.69

Численное интегрирование выполняется командой evalf(int(f, x=x1..x2), e), где e – точность вычислений (число

знаков после запятой).

Интегралы, зависящие от параметра. Ограничения для параметров

Если требуется вычислить интеграл, зависящий от параметра, то его значение может зависеть от знака этого параметра или каких-либо

+¥

других ограничений. Рассмотрим в качестве примера интеграл òe-ax dx ,

который, как известно из математического анализа, сходится при а>0 и расходится при а<0. Если вычислить его сразу, то получится:

> Int(exp(-a*x),x=0..+infinity)= int(exp(-a*x), x= 0..

+infinity);

Definite integration: Can't determine if the integral is convergent. Need to know the sign of --> a Will now try indefinite integration and then take limits.

¥					e ( -a x )	- 1
ó	e	( -a x )	dx = lim	-	e ( -a x )	- 1
ô
ô
ô					a
õ0			x ® ¥		a

Таким способом интеграл с параметром не вычислить. Для получения явного аналитического результата вычислений следует сделать какие-либо предположения о значении параметров, то есть наложить на них ограничения. Это можно сделать при помощи командыassume(expr1), где expr1 – неравенство. Дополнительные ограничения вводятся с помощью команды additionally(expr2), где expr2 – другое неравенство, ограничивающее значение параметра с другой стороны.

После наложения ограничений на параметрMaple добавляет к его имени символ (~), например параметр a, на который были наложены некоторые ограничения, в сроке вывода будет иметь вид: a~.

Описание наложенных ограничений параметраa можно вызвать командой about(a). Пример: наложить ограничения на параметр a такие,

что a>-1, a£3:

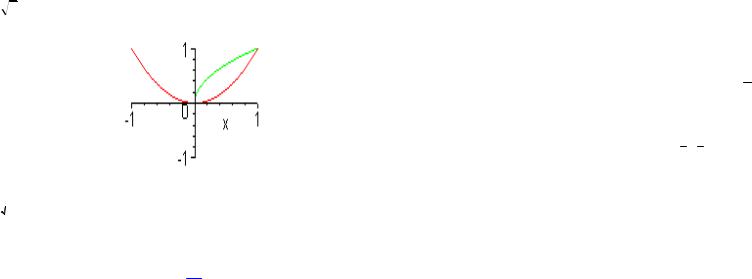
> assume(a>-1); additionally(a<=3);about(a);

be:

Для

вычисления двойных

интеграловòò f ( x, y)dxdy

используется

Originally a,

renamed

a~:

assumed to

RealRange(Open(-1),3)

+¥

команда Doubleint(f(x,

y),

D), где D –

область интегрирования,

Вернемся к вычислению интеграла с параметром òe-ax dx , которое

записываемая в одном из следующих форматов:

х2,

y1,

задают

следует производить в таком порядке:

x=х1..х2,

y=y1..y2, где

числа х1,

прямоугольную область интегрирования;

assume(a>0);

Int(exp(-a*x),x=0..+infinity)=int(exp(-

, где

f1(y),

f2(y)

линии,

a*x),x=0..+infinity);

x=f1(y)..f2(y), y=y1..y2

ограничивающие

область интегрирования слева

и справа

на интервале от

+¥

y1 до y2;

òe(-a ~ x)dx =

y=g1(x)..g2(x) , где

g1(y),

g2(y) -

a ~

x=х1..х2,

линии,

Двойные

интегралы,

сведенные

повторным

интегралам

ограничивающие область интегрирования снизу и сверху на интервале от

х1 до х2.

y 2( x)

òdx ò f (x, y)dy ,

вычисляются

конструкцией

Для

вычисления

тройных

интегралов f (x, y, z)dxdydz

y1( x)

òòò

int(int(f,y=y1(x)..y2(x)),	x=a..b).	Рассмотрим	пример:
Вычислить òò( x + 2 y)dxdy , где	область D ограничена кривыми		y = x2 ,
D

y = x .

> plot([x^2,sqrt(x)],x=-1..1,-1..1,color=[red,green]);

			Из	рисунка	видно, что	область	интегрирования	является
правильной как по x, так и по y. Сводим интеграл к повторному двойному
1
1		x
ò dx ò (x + 2 y)dy :
0	x2

> int(int(x+2*y,y=x^2..sqrt(x)),x=0..1);

ВMaple имеются две специальные команды для вычисления двойных

итройных интегралов, содержащиеся в библиотеке student.

используется команда Tripleint(f(x, y, z),x, y, z, V), где V

– область интегрирования.

Обе эти команды являются командами отложенного действия. Чтобы получить значение интеграла, следует использовать команду value(%).

Пример. Вычислить двойной интеграл òòsin(x + 2 y)dxdy по области,

ограниченной линиями y = 0, y = x, x + y = p . 2

>restart: with(student):

>J:=Doubleint(sin(x+2*y), x=y..Pi/2-y, y=0..Pi/2);

1p 1 p- y

J := ò	òsin( x + 2 y)dxdy
0	y
> J:=value(%);		2
	J :=	2
	J :=	3
		3
	1	1	2

Пример. Вычислить тройной интеграл òdx ò dyò(4 + z)dz .

-1 x 2 0

> J:=Tripleint(4+z, y=x^2..1,x=-1..1, z=0..2);

2 1 1

J := ò ò ò4 + zdydxdz

0 -1x 2

> J:=value(%);

Ротором вектор-функции F(x, y, z) называется вектор с координатами:

éæ

¶F

¶Fy ö æ

¶F

ö æ ¶Fy

¶F

öù

J :=

rotF = êç

÷,ç

÷ú . Ротор вычисляется командой

êç

¶y

¶z

÷ è

¶z

¶x ø ç

¶x

¶y

÷ú

ëè

øû

Векторный анализ

curl(F,[x,y,z],c).

Для вектор-функции F(x, y, z) можно вычислить матрицу Якоби с

Основные

дифференциальные

операции

векторного

анализа

помощью команды jacobian(F,[x,y,z]).

команды Maple для их вычисления содержатся в библиотеке linalg.

é¶F

¶Fy

¶F

Градиент

скалярной

функции f(x, y, z)

–

это

вектор,

координатами

¶x

¶x ¶x

которого являются частные производные по соответствующим переменным:

¶F

¶Fy

¶F

J =

¶f

¶y

Maple

ê ¶y

¶y ú

grad f ( x, y, z) =

÷ .

grad

вычисляется

одноименной

¶F

¶Fy

¶F

¶x

¶y

¶z

командой grad(f,[x,y,z],c), где здесь и в дальнейшемf – функция,

[x,y,z] – набор переменных, от которых она зависит.

дифференциальную

Рассмотрим

пример: Дана

функция u(x, y) = ln

Найти:

Параметр

позволяет

вычислять

данную

операцию в различных криволинейных координатах(по умолчанию

grad u( x, y) ;

углы,

которые

составляет

grad u

с осями

координат;

используется прямоугольная декартова система координат). Этот параметр

производную функции u(x,y) по направлению вектора q=[1,1].

может указываться

во

всех

имеющихся Mapleв

дифференциальных

> restart: with(linalg):

операциях.

Для

вычисления

дифференциальной

операции

цилиндрических координатах следует записатьcoords=cylindrical, в

Warning, new definition for norm

Warning, new definition for trace

сферических координатах – coords=spherical.

> u:=ln(y/x): g:=simplify(grad(u, [x, y]));

Лапласиан скалярной функции f(x, y, z)

–

это оператор, действующий

g :=

¶2 f

x y

на

функцию f(x, y, z)

по

правилу:

Df =

. Он вычисляется

> alpha:=simplify(angle(g, [1, 0]));

¶x2

¶y2

¶z2

командой laplacian(f,[x,y,z],c). Например, нужно найти значение

beta:=simplify(angle(g, [0, 1]));

параметра

а,

при

котором

+axy

удовлетворяет

уравнению

a := p - arccos ç

функция u=x

+ x

2 ÷

Лапласа Du=0

ç x

> u:=x^3+a*x*y^2: Delta(u):=laplacian(u, [x,y]);

b := arccos

D( x

+ a x y

) := 6 x + 2 a x

+ x

> a=solve(%=0,a);

ç y

a = -3

Косинусы

этих

углов

косинусами

Дивергенцией

вектор-функции

F(x, y, z)

называется

функция

являются

направляющими

¶Fy

grad u( x, y) . Убедимся, что сумма их квадратов равна единице.

(скалярная),

вычисляемая

по

правилу:

¶F

divF (x, y, z) =

> simplify(cos(alpha)^2+cos(beta)^2);

¶x +

¶y

+ ¶z .

Дивергенция в Maple вычисляется командой diverge(F,[x,y,z],c),

функции u

Производная

по

направлениюq

равна

скалярному

где

здесь

дальнейшемF

– вектор-функция, [x,y,z]

–

набор

произведению

градиента

этой

функции на нормированный векторq :

переменных, от которых она зависит.

¶u

= (gradu,

e) , где e =

- нормированный вектор q .

¶q

> q:=vector([1,1]);e:=normalize(q);

q := [ 1, 1 ]

e :=

> udq:=simplify(dotprod(g,e));

udq :=

2 ( -y + x )

2 x y

Вычисление суммы ряда и произведений

Конечные

и бесконечные

суммыåS(n) вычисляются командой

n =a

прямого исполнения sum и отложенного исполнения Sum. Аргументы этих команд одинаковые: sum(expr, n=a..b), где expr – выражение, зависящее от индекса суммирования, a..b – пределы индекса суммирования, указывающие, что суммировать следует от n=a до n=b.

Если требуется вычислить сумму бесконечного ряда, то в качестве

верхнего

предела вводится infinity.

Например, пусть требуется найти

полную

и частичную

суммы

рядаобщий

член которого равен:

an=

(3n - 2)(3n +1)

> restart: a[n]:=1/((3*n-2)*(3*n+1));

an:=

(3n - 2)(3n +1)

> S[N]:=Sum(a[n], n=1..N)=sum(a[n], n=1..N);

SN :=

= -

(3n - 2)(3n +1) 3 3N +1

n=1

> S:=limit(rhs(S[N]), N=+infinity);

S :=

Аналогичным образом вычисляются произведения Õ P(n) командами

product(P(n),n=a..b)

n=a

прямого

отложенного действийProduct

P(n),n=a..b). Пример: вычислить

бесконечное

произведение:

¥ n3 - 1

Õn =2 n3 + 1

> Product((n^3-1)/(n^3+1),n=2..infinity)=

product((n^3-1)/(n^3+1), n=2..infinity);

¥ n3 - 1 2 .

Õn =2 n3 + 1 = 3

Разложение функции в степенной ряд и ряд Тейлора

Разложение функции f(x) в степенной ряд в окрестности точки а f ( x) = C0 + C1( x - a) + C2 ( x - a)n + ... + O( xn )

осуществляется командой series(f(x), x=a, n), где а – точка, в окрестности которой производится разложение, n – число членов ряда.

Аналогичного действия командаtaylor(f(x), x=a, n) раскладывает функции f(x) в окрестности точкиx=a до порядка n-1 по формуле Тейлора.

Команды series и taylor выдают результат, имеющий тип series. Для того, чтобы иметь возможность дальнейшей работы с полученным разложением, его следует преобразовать в полином с помощью команды convert(%,polynom).

Функцию многих переменныхf(x1,…,xn) можно разложить в ряд Тейлора по набору переменных(x1,…,xn) в окрестности точки (a1,…,an) до порядка n с помощью команды mtaylor(f(x), [x1,…,xn], n). Эта

команда

находится

стандартной

библиотеке, поэтому

перед

использованием должна быть вызвана readlib(mtaylor). Рассмотрим

пример:

построить

на

одном

рисунке

графики

интеграла

вероятности

erf (x) =

2p òe-t 2 dt

и его разложения в ряд Тейлора в окрестности нуля.

> q:=taylor(erf(x),x,8); p:=convert(%,polynom);

q :=

x -

x3 +

x5 -

x7 + O( x8 )

21 p

p :=

2 x

2 x3

> plot({erf(x),p},x=-2..2,thickness=[2,2],

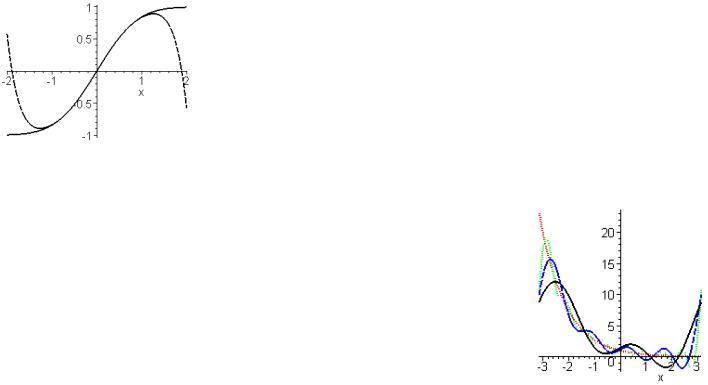
linestyle=[1,3], color=[red,green]);

ВMaple нет команды, позволяющей производить разложение функции

втригонометрический ряд Фурье. Однако можно создать собственную

процедуру разложения в ряд Фурье. Пусть требуется разложить на интервале [x1, x2] 2l-периодическую функцию f(x). Тогда ряд Фурье имеет вид:

				f ( x)
где		l = (x2		- x1 ) / 2 ;
1		x2	kpx	dx .
1		ò f ( x) sin	kpx
bk =
bk =	l		l
		x1

kpx

cos

bk sin

k =1

;

kpx

dx ;

ò f ( x)dx

a0 =

ak =

ò f ( x) cos

Получить первые n членов ряда Фурье можно с помощью следующей процедуры:

>fourierseries:=proc(f,x,x1,x2,n) local k, l, a, b, s;

>l:=(x2-x1)/2;

>a[0]:=int(f,x=x1..x2)/l;

>a[k]:=int(f*cos(k*Pi*x/l),x=x1..x2)/l;

>b[k]:=int(f*sin(k*Pi*x/l),x=x1..x2)/l;

>s:=a[0]/2+sum(a[k]*cos(k*Pi*x/l)+b[k]*sin(k*Pi*x/l), k=1..n);

>end;

Порядок	обращения	к	этой		процедуре:
fourierseries(f,x,x1,x2,n), где f – имя			функции,	разложение
которой требуется найти, где х – имя независимой переменной, где х1,
x2 – интервал разложения, где n – число членов ряда.
Пунктирной линией изображен графикn-частичной				суммы	ряда
Фурье, а сплошной –	самой функции. По	виду n-частичной		суммы	ряда
	53

Фурье в данном примере легко установить общий вид этого ряда:

	p	¥	sin kx
f ( x) =		- å
			k
2		k =1

Рассмотрим пример. Разложив		в ряд Фурье функциюf ( x) = e-x с

периодом 2p на интервале[p;-p]. Построим на одном рисунке графики функции и ее 2, 4 и 8 -частичных сумм ряда Фурье.

>f:=exp(-x);x1:=-Pi;x2:=Pi:

>fr1:=fourierseries(f,x,x1,x2,2):

>fr2:=fourierseries(f,x,x1,x2,4):

>fr3:=fourierseries(f,x,x1,x2,8):

>plot({f,fr1,fr2,fr3},x=x1..x2,color=[black, blue, green, red], thickness=2, linestyle= [1,3,2,2]);

Сплошной линией изображен график функции, пунктирными – графики n-частичных сумм ряда Фурье. Видно, что чем больше слагаемых ряда удерживать, тем ближе расположен график суммы ряда к графику самой функции.

Лабораторная работа №3

Исследование функции. Интегрирование

- 1 -

такой Необходимо провести полное исследование функции и построить ее график по общей схеме.

	x4		x + 2	3) f (x) =	x 4
1) f ( x) =		2) f (x) = ln
			x - 2
	(1 + x)3
				1+ x 3

f (x) =

x 2

f (x) =

x 2

+ 3x -

f (x) = x 2 - 4

1 -

f (x) =

+ 3x - 4

f (x) = e

1-x

1- e x

x - 2

10)

f (x) =

11)

f (x) =

x 3 + 2x 2 -5

12)

f (x) = arccos

1- x

3 - x

x 2

1- 2x

f (x )= th

13)

f (x) =

+ arctgx

14)

f (x) = lnç x +

15)

16)

f (x) = x

1 lnç x +

+ 4 ÷

17)

f (x)

= arcsin

1+ x 2

18)

f (x) = sin x 2

19)

f (x) = e x cos x

20)

f (x) = 8x 2 e -x2

- 2 -

Интегрирование

Напомним, что для функции y = f (x) объем тела вращения на отрезке [a, b] равен

p ò y2 dx ,

длина

дуги

на

этом же

отрезке

1 + y¢2 dx .

Формула

трапеций:

é y0 + yn

n -1

b - a

ò f (x )dx » h ê

+ å yi ú , где h =

-равноотстоящие ординаты кривой

y = f (x)

i =1

[a, b] .

n -1

на

отрезке

Формула

Симпсона

ò f (x )dx »

ê y0 + y2n +

4å y2i -1 + 2å y2i ú , где

i =1

h =

b - a

p / 2

sin x cos xdx

Найти определенный интеграл

, при условии

cos

x + b

sin

a>0, b>0.

+¥

-ax 2

Найти несобственный интеграл

- e

dx , при a>-1

x 2

2 dx

3) Вычислить по формуле трапеций ò и результат сравнить с точным

1 x

значением интеграла.

					5
4)	По формуле Симпсона	вычислить				интеграл x3 dx	и результаты
					ò
сравнить с точным значением интеграла.					1
сравнить с точным значением интеграла.
			+¥			sin(ax)cos(bx)dx
5)	Вычислить несобственный	интеграл ò				sin(ax)cos(bx)dx	при a>0 b>0
5)	Вычислить несобственный	интеграл ò				x	при a>0 b>0
для случаев a>b, a=b, a<b.				0
для случаев a>b, a=b, a<b.
	0,2	sin(3x)e- x		2
6)	Численно найти интеграл ò	sin(3x)e- x			dx , результат сравнить со
6)	Численно найти интеграл ò	x	4		dx , результат сравнить со
	0,1	x
	0,1

значением, найденным по формуле трапеций.

Найти несобственный интеграл ò

6x - x

- 8

Вычислить площадь фигуры, ограниченной линиями y = x2 и y = x + 2 .

Найти длину

дуги

линии y =

между

точками

пересечения

линии с осью Ox .

10)

Вычислить объем

тела, полученного

вращением

эллипса

= 1

вокруг оси Ox .

11)

Найти несобственный интеграл ò

1 - sin 2x

12)

Найти площадь, ограниченную параболой x = 2 y2

и линией y = x - 3 .

13)

Найти объем тела, получающегося от вращения вокруг осиOx одной

арки синусоиды y = sin x .

14)

Определите

площадь поверхности, образованной вращением

кривой

x2 + y2 = R2

вокруг оси Ox .

15)Найти площадь, ограниченную линиями x = 0 , y = 2 и y = x .

16)Найти длину дуги астроиды x = a cos3 t , y = a sin3 t .

17)	Определить длину дуги кривой y =				x2
						-1 , отсеченной осью Ox .
					2	-1 , отсеченной осью Ox .
					2
18)	Найти	площадь	криволинейной					трапеции, ограниченной	дугой
	гиперболы y = 1/ x ,		отрезком [1, x] и					соответствующими отрезками,
	параллельными оси Ox .
19)	Определить длину дуги кривой y = ln x							от x = 3 / 4 до x = 12 / 5 .
			6	2	dx
20)	Найти несобственный интеграл ò			x	dx		.
20)	Найти несобственный интеграл ò			3			.
			1	x	-8

Контрольные вопросы к лабораторной работе № 3

1.Что такое команды прямого и отложенного исполнения? Опишите их действия.

2.С помощью какой команды вычисляются пределы? Какие у нее параметры?

3.Какие команды позволяют найти производную функции?

4.	Опишите	команды,	позволяющие	исследовать	функцию	на
	непрерывность.
5.	Опишите	общую схему исследования функции и			построение	ее
	графика в Maple.
6.	Какие	команды	производят	аналитическое	и	численное
	интегрирование? Опишите их параметры.

7.С помощью каких команд вводятся ограничения на параметры для вычисления интегралов, зависящих от параметров?

Глава 4

Линейная алгебра

Основная часть команд для решения задач линейной алгебры содержится в библиотеке linalg.

Для определения вектора Mapleв используется команда vector([x1,x2,…,xn]), где в квадратных скобках через запятую указываются координаты вектора. Например:

> x:=vector([1,0,0]);

x := [ 1, 0, 0]

Координату уже определенного вектора x можно получить в строке вывода, если ввести команду x[i] , где i - номер координаты.

Вектор можно преобразовать в список, наобороти, с помощью команды convert(vector, list) или convert(list, vector).

Сложить два вектора a и b можно с помощью двух команд: 1) evalm(a+b);

2)linalg[matadd] (a,b).

Команда		add	позволяет	вычислять			линейную		комбинацию
векторов a и b:	aa + bb , где a,b - скалярные величины, если использовать
формат: matadd(a,b,alpha,beta).							n
							n
Скалярное		произведение двух		векторов (a, b) = åaibi				вычисляется
							i =1
командой dotprod(a,b). Векторное произведение двух векторов [a, b]
вычисляется командой crossprod(a,b). Угол между двумя векторами
a и b вычисляется с помощью команды angle(a,b).
Норму (длину)			вектора a = ( x ,..., x		n	) в Rn	можно	вычислить с
			1		n
помощью команды norm(а,2). Нормировать вектор а можно с помощью
команды normalize(a).
Если	имеется		система n векторов {a1, a2 ,...,an } , то					с	помощью
команды basis([a1,a2,…,an]) можно найти базис этой системы. При
помощи	команды GramSchmidt([a1,a2,…,an])								можно

ортогонализовать систему линейно-независимых векторов {a1, a2 ,...,an } (по процедуре Грамма-Шмидта).

Действия с матрицами

Для определения матрицы вMaple можно использовать команду matrix(n, m, [[a11,a12,…,a1n],[a21,a22,…,a2m],…,[an1, an2,…, anm]]), где n - число строк, m – число столбцов в матрице. Эти числа задавать необязательно, а достаточно перечислить элементы матрицы построчно в квадратных скобках через запятую. Например:

> A:=matrix([[1,2,3],[-3,-2,-1]]);

é	1	2	3ù
A := ê		- 2	ú
ë- 3		- 2	-1û

В Maple матрицы специального вида можно генерировать с помощью дополнительных команд. В частности диагональную матрицу можно получить командой diag. Например:

> J:=diag(1,2,3);

	é1	0	0ù
J :=	ê0	2	0ú
	ê		ú
	ê	0	ú
	ë0	0	3û

Генерировать матрицу можно с помощью функцииf(i, j) от переменных i, j – индексов матрицы: matrix(n, m, f), где n - число строк, m – число столбцов. Например:

> f:=(i, j)->x^i*y^j;

f := (i, j) ® xi y j

> A:=matrix(2,3,f);

é	xy	xy2	xy3 ù
A := ê			x2 y	3	ú
êx2 y x2 y2			x2 y	3	ú
ë					û

Число строк в матрицеА можно определить с помощью команды rowdim(A), а число столбцов – с помощью команды coldim(A).

Сложение двух матриц одинаковой размерности осуществляется теми же командами, что и сложение векторов: evalm(A+B) или matadd(A,B). Произведение двух матриц может быть найдено с помощью двух команд:

1)evalm(A&*B);

2)multiply(A,B).

В качестве второго аргумента в командах, вычисляющих произведение, можно указывать вектор, например:

> A:=matrix([[1,0],[0,-1]]);B:=matrix([[-5,1],

[7,4]]); v:=vector([2,4]);

é1	0ù
A := ê	ú
ê	ú
ë0	-1û
é-5 1ù
B := ê	ú
ê	ú
ë 7	4û

v:= [ 2, 4 ]

>multiply(A,v); multiply(A,B); matadd(A,B);

[ 2, -4 ]

é-5	1ù
ê	ú
ê	ú
ë-7	-4û
é-4	1ù
ê	ú
ê	ú
ë 7	3û

Команда evalm позволяет также прибавлять к матрице число и умножать матрицу на число. Например:

> С:=matrix([[1,1],[2,3]]):evalm(2+3*С);

é5	3ù
ê	ú
ê	ú
ë6	11û

Определитель матрицы А вычисляется командойdet(A). Команда minor(A,i,j) возвращает матрицу, полученную из исходной матрицы А вычеркиванием i-ой строки и j-ого столбца. Минор Mij элемента aij матрицы А можно вычислить командойdet(minor(A,i,j)). Ранг матрицы А вычисляется командой rank(A). След матрицы А, равный сумме ее диагональных элементов, вычисляется командой trace(A).

>A:=matrix([[4,0,5],[0,1,6],[3,0,4]]);det(A);trace(A);

é4		0	5ù
ê			ú
ê	0	1	ú
A := ê	0	1	6ú
ê	3	0	ú
ë	3	0	4û

> minor(A,3,2);det(%);

Обратную матрицу А-1

1)evalm(1/A);

2)inverse(A).

Транспонированную

	1
	9
é 4	5ù
ê	ú
ê	ú
ë 0	6û
	24
можно вычислить двумя способами:
матрицу		можно	вычислить	командой
	61

transpose(A). Рассмотрим пример: используя заданную в предыдущем пункте матрицу А, найдем ей обратную и транспонированную:

> inverse(A); multiply(A,%); transpose(A);

é	4	0	-5ù
ê		1		ú
ê18			-24ú
ê				ú
ê		0		ú
ë -3			4û
é 1		0	0 ù
ê				ú
ê	0	1	0	ú
ê				ú
ê	0	0	1	ú
ë				û
é4		0	3ù
ê				ú
ê	0	1		ú
ê			0ú
ê				ú
ê	5	6		ú
ë			4û

Выяснить положительную или отрицательную определенность матрицы можно при помощи командыdefinite(A,param), где param может принимать значения: 'positive_def' – положительно определена (A>0), 'positive_semidef' – неотрицательно определенная

( A ³ 0) , 'negative_def'	– отрицательно	определенная (A<0),
'negative_semidef' -	неположительно	определенная( A £ 0) .

Результатом действия будет константаtrue – подтверждение, false – отрицание сделанного предположения. Например:

>A:=matrix(2,2,[2,1,1,3]);definite(A,'positive_def');

		é 2	1ù
	A := ê		ú
		ê	ú
		ë 1	3û
		true
Проверить	ортогональность				матрицыА	можно	командой
orthog(A).
>В:=matrix([[1/2,1sqrt(3)/2],[1sqrt(3)/2,-1/2]]);
orthog(В);	é	1	3		ù
	ê				ú
	ê				ú
	ê	2	2		ú
	ê	2	2		ú
	Â := ê				ú
	ê	3		-1	ú
	ê	3		-1	ú
	ê	2	2		ú
	ë	2	2		û

true

Возведение матрицы А в степеньn производится командой

evalm(A^n). Вычисление матричной экспонентыe A возможно с помощью команды exponential(A). Например:

>С:=matrix([[5*a,2*b],[-2*b,5*a]]);exponential(Т); evalm(Т^2);

é 5 a

2 bù

C := ê

ë-2 b

5 aû

( 5 a + 2 I b )

( 5 a - 2 I b )

I e

( 5 a - 2 I b )

1 ( 5 a - 2 I b ) 1 ( 5 a + 2 I b )

1 ( 5 a + 2 I b )

I e

ê- I e

é25 a2 - 4 b2

20 a b ù

-20 a b

25 a

2ú

- 4 b û

-	1	I	e	( 5 a + 2 I b )ù
					ú
	2				ú
	2				ú
					ú
	1		( 5 a - 2 I b )		ú
	1		( 5 a - 2 I b )		ú
+		e			ú
					ú
	2				ú
	2				û

Спектральный анализ матрицы

Из курса линейной алгебры известно, что если Ах=lх, то вектор х называется собственным вектором матрицыА, а число l – собственным числом, соответствующим данному собственному вектору. Совокупность всех собственных чисел матрицы называется спектром матрицы. Если в спектре матрицы одно и тоже собственное число встречаетсяk раз , то говорят, что кратность этого собственного числа равна k.

Для нахождения собственных чисел матрицыА используется команда eigenvalues(A). Для нахождения собственных векторов матрицы А используется командаeigenvectors(A). В результате

выполнения	этой	команды		будут	получены собственные , числаих
кратность и соответствующие собственные векторы.
Чтобы понять, в каком виде получаются результаты выполнения
команды eigenvectors,			внимательно			разберитесь		со	следующим
примером:	матрица	é 3	-1	1ù	имеет 3		собственных		вектора:
		A = ê-1	5	-1ú
		ê		ú
		ê	-1	ú
		ë 1		3û
a1 = (-1, 0,1) , отвечающий собственному числу l1 = 2							кратности 1, a2 = (1,1,1) ,
отвечающий	собственному		числу l2 = 3			кратности 1,		a3 = (1,-2,1) ,

отвечающий собственному числу l3 = 6 кратности 1. Найдем их в Maple:

>A:=matrix([[3,-1,1],[-1,5,-1],[1,-1,3]]): eigenvectors(A);

[ 2, 1, { [ -1, 0, 1 ] } ], [ 6, 1, { [ 1, -2, 1 ] } ], [ 3, 1, { [ 1, 1, 1 ] } ]

Минимальный многочлен (делитель) матрицы А можно найти с помощью команды minpoly(A,lambda).

Привести матрицу А к нормальной форме Жордана можно командой jordan(A).

Ктреугольному виду матрицуА можно привести тремя способами:

1)команда gausselim(A) приводит матрицу А к треугольному виду

методом Гаусса;

2)команда ffgausselim(A) приводит матрицу А к треугольному виду методом Гаусса без деления. Эта команда предпочтительней для работы с символьными матрицами, так как не производит нормировку элементов и исключает возможные ошибки, связанные с делением на нуль;

3)команда gaussjord(A) приводит матрицу А к треугольному виду

методом Гаусса-Жордана.		F ( A) = lE - A можно
Характеристическую	матрицу	F ( A) = lE - A можно			вычислить
командой charmat(A,lambda).		é3		-4	0	2ù
		é3		-4	0	2ù
		ê				ú
Рассмотрим пример.	Найти	для матрицы A = ê	4	-5	-2	4ú
		ê0		0	3	-2ú
		ê	0	0	2	ú
		ê	0	0	2	-1ú
		ë				û

собственные значения и собственные вектора, привести ее к жордановой нормальной форме J , найти матрицу перехода S и выполнить проверку по правилу SJ = AS .

> with(linalg):A:=array([[3,-4,0,2],[4,-5,-2,4],

[0,0,3,-2],[0,0,2,-1]]);

Warning, the protected names norm and trace have been redefined and unprotected

é3	-4	0	2ù
ê			ú
ê	-5	-2	ú
ê4	-5	-2	4ú
A := ê	0	3	ú
ê0	0	3	-2ú
ê			ú
ê	0	2	ú
ë0	0	2	-1û

Найдем собственные числа и собственные векторы: > eigenvectors(A);

В строке вывода перечислены в квадратных скобках собственное				[ 1, 2, { [ 1, 1, 1, 1 ] } ], [ -1, 2, { [ 1, 1, 0, 0 ] } ]
число, его кратность и соответствующий собственный вектор в фигурных				Рассмотрим	корневое	подпространство, отвечающее l = 1.
скобках , затем следующие наборы таких же данных.			многочлена	( A - E )2 X = 0, Þ
Для	вычисления	характеристического	многочлена	> E:=array([[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]]):
PA (l) = det(lE - A)	матрицы A	используется	команда	> E:=array([[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]]):
charpoly(A,lambda).				evalm((A-E)^2);
charpoly(A,lambda).
	63					64

é-12		16	12		-16ù
ê						ú
ê		20	16			ú
ê-16		20	16		-20ú
ê	0	0	0			ú
ê	0	0	0		0ú
ê						ú
ê	0	0	0			ú
ë	0	0	0		0û
Получаем систему уравнений			ì3x		- 4x		- 3x		+ 4x		= 0,
Получаем систему уравнений			í	1		2		3		4	. Отсюда
			î4x1 - 5x2 - 4x3 + 5x4 = 0

> solve({3*x1-4*x2-3*x3+4*x4=0,4*x1-5*x2-4*x3+5*x4=0},

{x1,x2});

{ x2 = x4, x1 = x3 }

x1	x2	x3	x4
x1
1	0	1	0	a1
0	1	0	1	a2

a1 и a2	- корневые векторы. Максимальная высота вектора a1 может быть
равна	2, для	чего	должно	быть		(	) 1
равна	2, для	чего	должно	быть		выполнено условиеA - E	a ¹ 0 .
Проверим
> a1:=vector([1,0,1,0]):evalm((A-E)&*a1);
			[ 2, 2, 2, 2 ]
	Итак, базисный вектор e2			= a1 , e1		= (A - E )e2 .
> e2:=a1:e1:=evalm((A-E)&*e2);
			e1 := [ 2, 2, 2, 2 ]
	Рассмотрим		корневое		подпространство, отвечающее		l = -1 .
( A + E )2 X = 0,		Þ
> evalm((A+E)^2);			é0	0	12	-8ù
			é0	0	12	-8ù
			ê	0	8	ú
			ê0	0	8	-4ú
			ê			ú
			ê	0	12	ú
			ê0	0	12	-8ú
			ê			ú
			ê	0	8	ú
			ë0	0	8	-4û

b1 и b2 - корневые векторы. Построим канонический базис: высота вектора b1 может быть равна 2, но для этого должно выполняться условие ( A + E )b1 ¹ 0 . Проверим

> b1:=vector([1,0,0,0]):evalm((A+E)&*b1);

[ 4, 4, 0, 0 ]

e3 = (A + E ) e4 .

Значит b1

имеет высоту 2 и отсюда e4

= b1 ,

> e4:=b1:e3:=evalm((A+E)&*e4);

e3 := [ 4, 4, 0, 0 ]

é1

0 ù

Отсюда:

. Проверим,

что

это действительно так:

ê0

-1

ë0

0 0 -1û

SJ = AS , где S

матрица

перехода,

формируемая из векторов

e1 , e2 , e3 , e4 .

> Rez:=evalm(evalm(S&*J)-evalm(A&*S));

é0

0ù

Rez :=

ê0

0ú

ê0

0ú

ë0

0û

И теперь воспользуемся командой jordan(A):

> jordan(A);

é-1

0ù

-1

0ú

ê 0

1ú

1û

Видим, что полученная нами	матрицаJ совпадает	с jordan(A)
точностью до перестановки клеток.
Системы линейных уравнений и матричные уравнения
Система линейных	уравнений Ax = b может	быть решена

несколькими способами.

Способ 1: стандартная команда solve находит решение системы линейных уравнений, записанных в развернутом виде:

ìa

x + a x

+ ... + a

= b

11 1

í..........

..........

.......

ïa

+ a

+ ... + a

= b

Способ 2: команда linsolve(A,b) из пакета linalg находит решение уравнения Ax = b . Аргументы этой команды: А – матрица, b – вектор.

С помощью командыlinsolve(A,b) можно найти решение матричного уравнения АХ=В, если в качестве аргументов этой команды указать, соответственно, матрицы А и В.

> A:=matrix([[1,2],[1,3]]);b:=vector([1,-2]); linsolve(A, b);

é 1		2ù
A := ê		ú
ê	1	ú
ë	1	3û

b := [ 1, -2]

[ 7, -3 ]

Способ 3: команда leastsqrs(A,b), которая позволяет получить приближение к решению данного уравнения по методу наименьших квадратов.

> restart: with(linalg):A := array([[1,-1,1],[1,1,-

2],[2,0,-1]]);b := vector([1,2,4]);leastsqrs(A,b);

Warning, the protected names norm and trace have been redefined and unprotected

			é1	-1		1ù
			ê		1	-2		ú
			A := ê1		1	-2		ú
			ê					ú
			ê		0	-1		ú
			ë2		0	-1		û
			b := [ 1, 2, 4 ]							11
é	_t		, -5 + 3 _t		, 2 _t				-	11	ù
ê		1		1			1				ú
ê											ú
ê										3	ú
ë										3	û

> leastsqrs(A,b,'optimize');

é	67		-3		-10 ù
ê		,		,		ú

ê	42		14		21	ú
ë						û

Ядро матрицы А – это множество таких векторовх, произведение

матрицы	А на которые равно нулевому вектору: Ax = 0 . Поиск	ядра
матрицы	А эквивалентен решению системы линейных	однородных
уравнений. Найти ядро матрицы А можно командой kernel(A).

Лабораторная работа №4

Линейная алгебра

- 1 -

Для приведенной матрицы A													найти AT					,	det A , A-1 .			Найти
собственные значения и собственные вектора,																	привести матрицу A к
жордановой					нормальной					форме J ,			найти			матрицу				перехода S и
выполнить проверку по правилу SJ = AS .
é4 -3 1 2ù													é-3 0 0 4ù
ê							ú						ê							ú
1) A = ê5				-8 5 4ú								2) A = ê			0		-2 0 3ú
ê6 -12 8 5ú													ê 0				0 1 1ú
ê							ú						ê		0		0			ú
ê				-3			ú						ê		0		0		0 1ú
ê1				-3		2 2ú							ë							û
ë							û
é 1					1	0 1				1 ù			é1				2		-14 0 -8 ù
ê		-1			3	0 1				1	ú		ê		3 2				1 3	0 8		ú
ê		-1			3	0 1				1	ú		ê		3 2				1 3	0 8		ú
ê					-2 2		1				ú	4) A = ê0 -1							7	1 0 ú
3) A = ê 2					-2 2		1			-1ú		4) A = ê0 -1							7	1 0 ú
ê											ú		ê		2		-3		10	4	8	ú
ê		-1			1	0	1			0	ú		ê		2		-3		10	4	8	ú
ê		-1			1	0	1			0	ú		ê				-3		8 -2 13			ú
ê		-1			1	0	-1			2	ú		ë1				-3		8 -2 13			û
ë		-1			1	0	-1			2	û
é-7 -33 5 -17 -17ù													é 3 6 -10 -6 14ù
ê	8			26 -4			9			9	ú		ê		2 4				5		ú
ê	8			26 -4			9			9	ú	6)	ê		2 4				5	3 -7 ú
5) A = ê 0				0		9	0			0 ú		6)	A = ê 2 -1 10							1 -5ú
ê	0			-1 1			8			-1	ú		ê	-1 0							ú
ê	0			-1 1			8			-1	ú		ê	-1 0					-1 7 2 ú
ê							-8			1	ú		ê	-1 2 -3 -2 11ú
ë-8 -16 2							-8			1	û		ë								û
é13 4 5 -6 20ù													é13 4 5 -6 20ù
ê	0 6 0 1 2								ú				ê		0 6 0 1 2						ú
ê	0 6 0 1 2								ú				ê		0 6 0 1 2						ú
7) A = ê-2 -1 5 1 -8 ú												8) A = ê-2 -1 5 1 -8 ú
ê	3 2 3 3 6								ú				ê		3 2 3 3 6						ú
ê	3 2 3 3 6								ú				ê		3 2 3 3 6						ú
ê									ú				ê								ú
ë-1 0 0 1 2									û				ë-1 0 0 1 2								û
é 8 1 0 2 -4 ù														é-3 1 3 -6ù
ê								ú						ê						ú
ê	-3			4	0	-1	4	ú				10) A =		ê-5				2	4	-8ú
9) A = ê 2 1 4 0 -2 ú														ê 0 -2 3 -1ú
ê	-1 2 1 4 3							ú						ê		1				ú
ê	-1 2 1 4 3							ú						ê		1		-1 0 2 ú
ê								ú						ë						û
ê			2		0	1		ú
ë3			2		0	1	2û
é13 4 5 -6 20 ù														é1 -4 4 -3ù
ê 0				6	0	1	2 ú							ê			-1		2	ú
ê							ú							ê0			-1		2	-1ú
ê							ú					12) A = ê								ú
11) A = ê-2				-1	5	1	-8 ú					12) A = ê				0	-1		2	ú
ê 3				2	3	3	6 ú							ê		0	-1		2	-1
ê 3				2	3	3	6 ú							ê						ú
ê	-1 0 0					1 2 ú								ê0 0 1 -1ú
ë							û							ë						û

é 2 -1 0 -4ù

é6 -2 -4 2ù

13)

A = ê-2

-4 1

2 ú

14)

A = ê8

-2

-7

2ú

ê10 -1 -3 -9ú

ê2 -1

0 1ú

-1 0 -2ú

ê0 0

0 1ú

é 9 -8

8 0

1ù

é 8 1 0 2 - 4ù

-1

15)

-16 24 4 - 21ú

16)

ê- 3 4 0

4ú

A = ê

-16

-15ú

A = ê

- 2ú

-8 4

-1 2 1 4

ê- 2

7ú

3ú

-1

- 4 0

3 2 0

11û

2û

é 9

5 - 2 0

3ù

é4

3 -1 - 2 0ù

-1

6 0

17)

2 0 - 3ú

18)

ê0

1 0ú

A = ê-8

- 5

- 2ú

A = ê1

- 2

0ú

- 7

1 0

ê-8

0 1 -1ú

ê0

4 0ú

- 4

- 4 0

ë-8

1 1 - 2û

ë0

1 2û

é3 -4 0 2 ù

é4 -3 1 2ù

19)

A = ê4

-5

-2

20)

A = ê5

-8

4ú

ê0 0 3 -2ú

ê6 -12 8 5ú

ê0 0 2

-1ú

ê1

-3 2 2ú

- 2 -

Решить матричное уравнение АХ=В. Проверить результат,

пользуясь формулой EX = A-1 B

é1 2ù

, B =

é3 5ù

é1 2ù

é3 5ù

A = ê

ú , B = ê

ë3 4û

ë5 9û

ë3 4û

ë5 9û

é1 2ù

, B

é 1 -3ù

é3 2 ù

, B =

é 7 ù

A = ê

ê ú

ë3 2û

ë10 2 û

ë4

- 5û

é5 2ù

, B

é4ù

é4 -3ù

, B =

é 17 ù

A = ê

ê ú

A = ê

ë7 4û

ë8

ë2 5 û

ë-11û

A =

ém - nù

2 ù

é2 -1 1ù

é 2 ù

, B = ê(m - n)

A =

3 2 2

B =

-2

ë2

-1û

при m ¹ 2n

-2

ë1

é1 2 3 ù

é5ù

é1 2 3 ù

é 4 ù

A =

B =

10)

A =

B =

ê2

-1 -1ú

ê1

-1ú

3 3 2

ë1 3 4 û

ë6û

ë10

11)

A =

é4 3ù

B =

é5ù

12)

A =

é2 7ù

B =

é 8 ù

ú ,

ë5 2û

ë8û

ë6 5û

ë-8û

13)

A =

é9 2 ù

é 3 ù

14)

A =

é3 2ù

B =

é7ù

ë7

-2û

ë13û

ë4 3û

ë8û

В заданиях 15-18 определить

значения параметра l , при которых

система имеет решения.

15)

A =

é6l 2ù

é5ù

16)

A =

él 2 ù

é3ù

ë 9 3û

ë7

8 4lû

ë9

17)

A =

él2

3lù

é4ù

18)

A =

él - 3ù

é1ù

, B = ê

ë 3

ë6

ël - 2û

2û

19)

A =

é3 2ù

B =

é7ù

20)

A =

é-2 4ù

é2ù

ú ,

B = ê

ë4 3û

ë8û

1 3û

ë4û

Контрольные вопросы к лабораторной работе № 4

Какой

пакет

следует

загрузить

перед

решением

задач линейной

алгебры в Maple?

2.С помощью каких команд можно ввести вектор, матрицу?

3.Какими двумя командами можно сложить два вектора одинаковой размерности? 2 матрицы?

4. Какие виды произведений векторов вычисляютсяMaple и какие

команды для этого используются?

5.Как вычислить норму вектора?

6.Как вычислить угол между двумя векторами?

7.Опишите команды нахождения базиса системы векторов и построение ортогонального базиса системы векторов.

8.	Какими	двумя	командами	можно вычислить произведение двух
матриц (или матрицы на вектор)?
9.	Какие команды используются для нахождения определителя, минора,
алгебраического дополнения, следа матрицы?
10.	Какая	матрица	называется	обратной и какими способами она
вычисляется в Maple?

11.Какие команды используются для нахождения спектра матрицы и ее собственных векторов? В каком виде Mapleв выводятся результаты выполнения этих команд?

12.Перечислите специальные виды матриц и команды, приводящие матрицы к этим формам.

13.Какая команда позволяет решать матричные уравнения?

Глава 5

Обыкновенные дифференциальные уравнения

Общее решение обыкновенных дифференциальных уравнений

Для нахождения аналитических решений ОДУ вMaple применяется
команда dsolve(eq,var,options),				где eq –	дифференциальное
уравнение,	var – неизвестные		функции, options – параметры.
Параметры	могут	указывать	метод	решения	,задачинапример, по
умолчанию	ищется	аналитическое		решение: type=exact. При

составлении дифференциальных уравнений для обозначения производной

применяется

команда

diff,

например,

дифференциальное

уравнение

y''+y=x записывается в виде: diff(y(x),x$2)+y(x)=x.

Общее

решение

дифференциального

уравнения

зависит

от

произвольных

постоянных,

число

которых

равно

порядку

дифференциального уравнения. В Maple такие постоянные, как правило,

обозначаются как _С1, _С2, и т.д.

Общее

решение

неоднородного

линейного

дифференциального

уравнения всегда выводится так, чтобы была четко видна, структура этого

решения. Как

известно,

общее

решение

неоднородного

линейного

дифференциального

уравнения

равно

сумме

общего

решения

соответствующего однородного дифференциального уравнения и частного

решения этого же неоднородного дифференциального уравнения. Поэтому в

строке вывода решение неоднородного линейного дифференциального

уравнения всегда состоит из слагаемых, которые содержат произвольные

постоянные

(это

общее

решения

соответствующего

однородного

дифференциального

уравнения),

слагаемых

без

произвольных

постоянных

(это

частное

решения

этого

же

неоднородного

дифференциального уравнения).

Команда dsolve

выдает

решение

дифференциального

уравнения в

невычисляемом формате. Для того, чтобы с решением можно было бы работать далее (например, построить график решения) следует отделить правую часть полученного решения командойrhs(%). Рассмотрим несколько примеров.

Найти общее решение дифференциального уравнения второго порядка y''-2y'+y=sinx+e-x.

>restart;

>deq:=diff(y(x),x$2)-2*diff(y(x),x)+y(x) =sin(x)+exp(-x);

deq:=

æ ¶

(-x)

y(x)

- 2ç

y(x)÷

+ y(x) = sin(x) + e

¶x

è ¶x

> dsolve(deq,y(x));

y( x) = _ C1ex + _ C2ex x +

cos( x) +

e(-x)

Найти общее решение дифференциального уравнения порядка y''+k2y=sin(qx) в двух случаях: q¹k и q=k (резонанс).

> restart; de:=diff(y(x),x$2)+k^2*y(x)=sin(q*x);

de:=

¶2

¶x

2 y( x)

+ k

y(x) = sin(qx)

> dsolve(deq,y(x));

1 cos(( k - q) x) ö

1 cos((k + q) x)

ç-

÷sin( kx)

k + q

k - q

y( x) =

1 sin(( k

- q) x)

1 sin(( k + q)x)

÷cos( kx)

2 k - q

k + q

+ _ C1sin(kx) + _ C2 cos( kx)

Теперь найдем решение в случае резонанса. Для этого перед вызовом команды dsolve следует приравнять q=k.

> q:=k: dsolve(de,y(x));

1 cos(kx)2 sin( kx)

cos(kx) sin( kx) +

kx ÷ cos(kx)

y(x) = -

k 2

_ C1sin( kx) + _ C2 cos(kx)

Фундаментальная (базисная) система решений

Команда

dsolve

предоставляет

возможность

найти

фундаментальную

систему

решений(базисные

функции)

дифференциального уравнения. Для этого в параметрах командыdsolve

следует указать output=basis.

Пример: Найти фундаментальную систему решений дифференциального

уравнения: y(4)+2y''+y=0.

> de:=diff(y(x),x$4)+2*diff(y(x),x$2)+y(x)=0;

de:=

y(x)÷

+ 2ç

y( x)÷

+ y(x) = 0

¶x

> dsolve(de, y(x), output=basis);

[cos( x),sin(x), x cos( x), x sin(x)]

Решение задачи Коши или краевой задачи

Команда dsolve может найти решение задачи Кошиили краевой задачи, если помимо дифференциального уравнения задать начальные или краевые условия для неизвестной функции. Для обозначения производных в

начальных

или

краевых

условиях

используется дифференциальный

оператор

D ,

например,

условие

y''(0)=2 следует

записать в

виде

(D @@ 2)( y)(0) = 2 ,

или условие y'(1)=0:

D( y)(1) = 0 .

Напомним,

что

производная n-го порядка записывается в виде (D @@ n)( y) .

Пример:

Найти

решение

краевой

задачи: y''+ y = 2x - p , y(0) = 0 ,

æ p ö

yç

÷ = 0

. Построить график решения.

è 2 ø

> restart; de:=diff(y(x),x$2)+y(x)=2*x-Pi;

¶2

de:= ç

y(x)÷ + y(x) = 2x - p

¶x

> cond:=y(0)=0,y(Pi/2)=0;

æ p ö

cond := y(0) = 0, yç

÷ = 0

2 ø

> dsolve({de,cond},y(x)); y(x)=2x-p+pcos(x)

Для построения графика решения предварительно следует отделить правую часть полученного выражения.

> y1:=rhs(%):plot(y1,x=-10..20,thickness=2);

Команда dsolve может найти решение системы дифференциальных

уравнений	(или	задачи	),Кошиесли	в	ней	: указать
dsolve({sys},{x(t),y(t),…}),			где sys	-		система

дифференциальных уравнений, x(t),y(t),… - набор неизвестных функций.

Пример: Найти решение системы дифференциальных уравнений:

ì					2
ïx¢ = -4x - 2 y	+					,
ïx¢ = -4x - 2 y	+		e	t	-1	,
ï			e		-1
í			3
ïy¢ = 6x + 3y -			3
ïy¢ = 6x + 3y -			t
ï		e	t	-1
î		e		-1

>sys:=diff(x(t),t)=-4*x(t)-2*y(t)+2/(exp(t)-1), diff(y(t),t)=6*x(t)+3*y(t)-3/(exp(t)-1):

>dsolve({sys},{x(t),y(t)});


	{x(t) = -3 _ C1 + 4C1 _ e(-t) - 2C2 _+ 2C2 _ e(-t) + 2e( -t) ln(et - 1),
	y(t) = 6 _ C1 - 6 _ C1e-t - 3 _ C2e(-t) + 4 _ C2 - 3e( -t) ln(e(t)							-1)}
Приближенное решение дифференциальных уравнений с
		помощью степенных рядов
Для	большинства		дифференциальных			уравнений	не	может быть
найдено точное аналитическое решение. В этом случае дифференциальное
уравнение	можно	решить с		помощью		приближенных	методов, и, в
частности, с помощью разложения в степенной ряд неизвестной функции.
Чтобы найти приближенное решение дифференциального уравнения в
виде степенного ряда, в			команде dsolve			следует после	переменных
указать параметр type=series (или					просто series). Для		того, чтобы
указать	порядок	разложенияn,		т.е.	порядок степени,		до	которой
производить разложение,			следует	перед		командойdsolve		вставить
определение порядка с помощью команды Order:=n.

Если ищется общее решение дифференциального уравнения в виде разложения в степенной ряд, то коэффициенты при степеняхх найденного разложения будут содержать неизвестные значения функции в нулеy(0)

и ее производных D(y)(0), (D@@2)(y)(0) и т.д. Полученное в строке вывода выражение будет иметь вид, похожий на разложение искомого решения в ряд Маклорена, но с другими коэффициентами при степеняхх.

Для выделения частного	решения следует задать	начальные условия
y(0)=у1, D(y)(0)=у2,	(D@@2)(y)(0)=у3 и	т..д, причем

количество этих начальных условий должно совпадать с порядком соответствующего дифференциального уравнения.

Разложение в степенной ряд имеет seriesтип , поэтому для дальнейшей работы с этим рядом его следует преобразовать в полином с помощью команды convert(%,polynom), а затем выделить правую часть полученного выражения командой rhs(%).

Пример 1: Найти решение задачи Коши: y¢ = y + xe y , y(0) = 0 в виде степенного ряда с точностью до 5-го порядка.

>restart; Order:=5:

>dsolve({diff(y(x),x)=y(x)+x*exp(y(x)), y(0)=0}, y(x), type=series);


		y(x) =	1	x2 +	1	x3 +		1	x4 + O(x5 )
		2			6		6
Пример 2. Найти приближенное решение в виде степенного ряда 6до-го
порядка и точное решение задачи Коши:							y¢¢¢ - y¢ = 3(2 - x2 ) sin x ,			y(0) = 1 ,
¢	¢¢	= 1 . Построить на				одном рисунке графики				точного и
y (0) = 1 ,	y (0)	= 1 . Построить на				одном рисунке графики				точного и

приближенного решений.

>restart; Order:=6:

>de:=diff(y(x),x$3)-diff(y(x),x)=3*(2-x^2)*sin(x);

æ	¶3		ö	æ ¶	ö
de:= ç			y( x)÷	- ç	y(x) ÷	= 3(2 - x2 ) sin( x)
		3
ç	¶x		÷	è ¶x	ø
è			ø

> cond:=y(0)=1, D(y)(0)=1, (D@@2)(y)(0)=1; cond:=y(0)=1, D(y)(0)=1, D(2)(y)(0)=1

> dsolve({de,cond},y(x));

y(x)= 21 cos( x) - 3 x2 cos( x) + 6x sin( x) -12 + 7 e x + 3 e(-x) 2 2 4 4

>y1:=rhs(%):

>dsolve({de,cond},y(x), series);

y(x)= 1 + x + 1 x2 + 1 x3 + 7 x4 + 1 x5 + O(x6 ) 2 6 24 120

Тип решения дифференциального уравнения в виде ряда естьseries, поэтому для дальнейшего использования такого решения(вычислений или построения графика) его обязательно следует конвертировать в полином с помощью команды convert

>convert(%,polynom): y2:=rhs(%):

>p1:=plot(y1,x=-3..3,thickness=2,color=black):

>p2:=plot(y2,x=-3..3, linestyle=3,thickness=2, color=blue):

>with(plots): display(p1,p2);

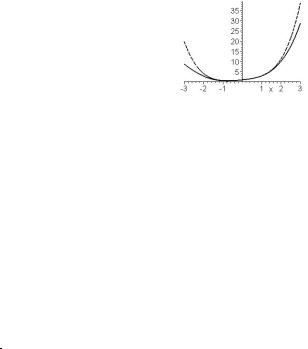
На этом рисунке видно, что наилучшее приближение точного решения степенным рядом достигается примерно на интервале -1<x<1.

Численное решение дифференциальных уравнений с помощью команды dsolve. Построение графиков решений дифференциальных уравнений с помощью команды odeplot

Для	того, чтобы	найти	численное	решение	дифференциального
уравнения (задачи Коши или краевой задачи) в команде dsolve следует
указать параметр type=numeric (или просто numeric). Тогда команда
решения дифференциального уравнения будет иметь видdsolve(eq,
vars,	type=numeric, options), где eq – уравнения, vars –
список	неизвестных	функций,	options –	параметры,	позволяющие

указать метод численного интегрирования дифференциального уравнения. Пользователю предлагается несколько базовых методов, каждый из которых имеет большое количество опций.

Название опции	Описание метода
method=rkf45	Метод Рунте-Кутта четвертого-пятого
	порядка (установлен по умолчанию).
method=dverk78	Метод Рунте-Кутта седьмого-восьмого
	порядка.
method=classical	Содержит несколько основных методов:
[метод]	foreuler -прямой метод Эйлера;
	heunform — усовершенствованный метод
	Эйлера;
	impoly — модифицированный метод
	Эйлера
	rk2 — классический метод Рунге-Кутта
	второго порядка;
	rk3 — классический метод Рунге-Кутта
	третьего порядка;
	rk4 — классический метод Рунге-Кутта
	четвертого порядка;
	adambash - метод Адамса-Башфорда
	77

(метод «прогноза»);

abmoulton — метод Адамса-Моултона

(метод «проглота и коррекции»).

method=gear

Одношаговый метод Гира

method=mgear

Многошаговый метод Гира

method=lsode

Метод решения Ливермора Стиффа

method=laplace

Метод решения дифференциальных

уравнений, содержащих функции Дирака

или Хевисайда, использующий

преобразование Лапласа

Пример 1.

>syst:=diff(y(x) ,x)=f(x)-y(x)-x, diff(f(x) ,x)=y(x);

func := {y(x), f(x)}:

syst :=

y( x ) = f( x ) - y( x ) - x,

f( x ) = y( x )

>Fout:=dsolve({syst,y(0)=0,f(0)=1},func, type=numeric,

method=classical[rk4]);

Fout := proc(x_classical) ... end proc

>Fout(1);

[ x = 1., f( x ) = 1.25897207848196824,y( x ) = 0.343731405015429647]

Пример 2.

>DifEqn1:=diff(y(t),t$2)+5*diff(y(t),t)+6*y(t)=

Heaviside(t);

æ d2

æ d

DifEqn1 := ç

y( t ) ÷ + 5 ç

y( t ) ÷

+ 6 y( t ) = Heaviside( t )

èdt

>dsolve({DifEqn1, y(0)=0, D(y)(0)=1}, y(t), method =

laplace);

( -2 t )

(-3 t )

y( t ) =

График численного решения дифференциального уравнения можно

построить

помощью

командыodeplot(dd,

[x,y(x)],

x=x1..x2),

где

качестве

функции

используется

команда

dd:=dsolve({eq,cond}, y(x), numeric) численного решения,

после нее в квадратных скобках указывают переменную и неизвестную

функцию [x,y(x)], и интервал x=x1..x2 для построения графика.

Пример 3.

Найти

численное и

приближенное

решение в

виде степенного

ряда	до 6-ого	порядка	задачи :
y' '-x sin( y) = sin 2x , y(0) = 0 , y'(0) = 1 .

Сначала найдем численное решение задачи Коши и построим его график.

>restart; Ordev=6:

>eq:=diff(y(x),x$2)-x*sin(y(x))=sin(2*x):

>cond:=y(0)=0, D(y)(0)=1:

>de:=dsolve({eq,cond},y(x),numeric);

de:=proc(rkf45_x)...end

Замечание: в строке вывода появляется сообщение о том, что при решении использован метод rkf45. Если необходимо получить значение решения при каком-то фиксированном значении переменнойх (заодно будет выведено значение производной решения в этой точке), например, при х=0.5, то следует набрать:

> de(0.5);

é	¶	ù
êx = .5, y( x) = .5449261153862630,		y( x) = 1.272503082225380ú
êx = .5, y( x) = .5449261153862630,	¶x	y( x) = 1.272503082225380ú
ë	¶x	û

>with(plots):

>odeplot(de,[x,y(x)],-10..10,thickness=2);

Теперь найдем приближенное решение задачи Коши в виде степенного ряда и построим графики численного решения и полученного степенного ряда в интервале их наилучшего совпадения.

> dsolve({eq, cond}, y(x), series)

y( x) = x + 1 x3 + 1 x4 - 1 x5 + O( x6 ) 3 12 15

>convert(%, polynom):p:=rhs(%):

>p1:=odeplot(de,[x,y(x)],-2..3, thickness=2, color=black):

>p2:=plot(p,x=-2..3,thickness=2,linestyle=3, color=blue):

>display(p1,p2);

Коши

Из графика видно, что наилучшее приближение решения степенным рядом достигается примерно на интервале -1<x<1.

Пример 4. Построить графики решений задачи Коши системы дифференциальных уравнений:

ìx		(t ) = 2 y (t )	sin t - x (t )- t,
ï	&		,	x (0) =1 , y (0) = 2 .
í	&		,	x (0) =1 , y (0) = 2 .
ïy (t )= x (t ).
î
> restart; cond:=x(0)=1,y(0)=2:
>			sys:=diff(x(t),t)=2y(t)sin(t)-x(t)-t,

diff(y(t),t)=x(t):

>F:=dsolve({sys,cond},[x(t),y(t)],numeric):

>with(plots):

>p1:=odeplot(F,[t,x(t)],-3..7, color=black, thickness=2,linestyle=3):

>p2:=odeplot(F,[t,y(t)],-3..7,color=green, thickness=2):

>p3:=textplot([3.5,8,"x(t)"], font=[TIMES, ITALIC, 12]):

>p4:=textplot([5,13,"y(t)"], font=[TIMES, ITALIC, 12]):

>display(p1,p2,p3,p4);

Структура DESol

В	том случае,	если Maple не может представить решение
дифференциального уравнения или системы в явном, можновиде
использовать специальный объект DESol: DESol(ODE, VAR, INI)
По данной команде для уравнения или системыODE относительно
неизвестной функции или функцийVAR с начальными даннымиINI
создается	специальная структура. Это своеобразное развитие функции
RootOf применительно к дифференциальным уравнениям. Объект DESol
можно интегрировать, дифференцировать, находить для него разложения и,
конечно, получать численное решение.
Рассмотрим на примере как использовать объектDESol для
получения приближенного решения разложением в ряд(команда series) и
построения	численного	решения. Зададим	уравнение	Дуффинга	и

начальные условия:

>de:=diff(y(x),x,x)+y(x)+y(x)^3=cos(x);

>ic:={y(0)=0,D(y)(0)=1};

ic := {y(0) = 0, D(y)(0) = 1}

Определим сам объект DESol

> des:=DESol(de,y(x),ic);

При попытке аналитического решения задачи Коши для данного уравнения область вывода останется пустой:

> dsolve({de} union ic, y(x));

Применим команду series для вычисления решения в виде ряда по степеням х, а полученное выражение преобразуем в полином при помощи команды convert:

> Poly:=convert(series(des,x=0),polynom);

Poly := x + 1	x 2 - 1	x 3 -	1 x 4 -	1 x 5
2	6		12	24

Затем сгенерируем процедуру численного решения:

> Y:=dsolve({de} union ic, y(x),type=numeric);

Y := proc(x_rkf45) ... end proc;

Теперь по команде odeplot из графического пакетаplots построим график численного решения, при помощи универсальной командыplot - график полинома, и полученные рисунки объединим командой display:

>pY:=plots[odep1ot](Y,[x,y(x)],0..2,color=black):

>pP:=plot(Polу,x=0..2,thickness=2,color=black):

>plots[display]({pY,pP},axes=boxed);

Пакет Detools

Пакет DEtools предназначен для квалифицированной работы с ОДУ, как например, определение типа ОДУ, преобразования ОДУ к другому виду, численного решения задачи Коши, построения графиков решения и

фазовых портретов. Коротко перечислим некоторые наиболее употребляемые команды. К ним относятся:

Denormal	Возвращает “нормализованную” форму диффе-
	ренциального уравнения.

DEplot	Построение плоских интегральных кривых и
	фазовых траекторий
DEplot3d	Построение пространственных интегральных
	кривых и фазовых траекторий.
Dchangevar	Замена переменных в обыкновенном диффе-
	ренциальном уравнении.
PDEchangecoords	Переход к другой системе координат в диффе-
	ренциальном уравнении в частных производ-
	ных.
PDEplot	Построение решения дифференциального урав-
	нения с частными производными.
autonomous	Определяет, является ли система дифференци-
	альных уравнений автономной.

convertAlg

Возвращает список коэффициентов дифферен-

æ d

y( x ) = _a &where

ê{

_b( _a ) ÷

_b( _a ) - m _b( _a ) l + 2 m _b( _a ) _a - _a = 0 },

циального уравнения.

è d_a

convertsys

Преобразует систему дифференциальных урав-

ü ù

нений к системе первого порядка.

{ _a = y( x ), _b( _a ) =

ï ú

y( x ) },

ïy( x ) = _a, x = ô

d_a + _C1 ï ú

ô_b( _a )

dfieldplot

Построение плоских полей направлений,

ï ú

þ û

определяемых ДУ или системой ДУ.

Определен тип уравнения 2-го порядка - уравнение Ван дер Поля. Решение

представлено специальной структурой ODESolStruc, которая появляется

phaseportrait

Построение фазовых траекторий или их

проекций на координатные плоскости.

в том случае, если для рассматриваемого дифференциального уравнения

reduceOrder

Применят метод понижения порядка к диффе-

был понижен порядок, но решение не было получено. Структура содержит

ренциальному уравнению.

термин &where и состоит из двух полей: функционального представления

Для

обучения

поиска

важную

роль

играет

команда

новых

переменных

списка

трех

множеств(редуцированное

odeadvisor,

которая

предоставляет

информацию

типе

дифференциальное

уравнение,

прямое

обратное

преобразования

переменных).

рассматриваемого

уравнения

или системы. Из-за невозможности даже

Для

преобразования уравнения(или

системы

уравнений) высокого

короткого описания типов точно решаемых уравнений ограничимся беглым

порядка

системе

уравнений

первого

порядка

служит

команда, работу

перечислением команд,

указывая

корневое

слово, если имеется

несколько

которой демонстрирует следующий пример:

видов уравнений (и команд) данного класса.

Пример 2.

Команды

анализа

уравнения

первого

порядка

включают

s_deq:=diff(y(t),t$2)=y(t)-x(t),

diff(x(t),t)=x(t);

следующие

типы: Абеля (Abel),

однородные (homogeneous),

Бернулли

init:=y(0)=1, D(y)(0)=2, x(0)=3; Dtools [convertsys]

(Bernoul1i), Риккати (Riccati) и др., а также линейные (1inear) и

({s_deq}, {init}, {x(t),y(t)}, t, y, y_p);

точно решаемые

уравнения(exact),

вычисляемые

квадратурах

(quadrature),

допускающие

разделение переменных(separable),

s_deq :=

y( t ) = y( t ) - x( t ),

x( t )

= x( t )

dt2

дробно-рациональной

правой

частью(rational) и т.

д. Для решения

init :=y(0) =1, D(y)(0) =2, x(0) =3

уравнений

второго

порядка

имеются

команды, ориентированные как

на

отдельные важные уравнения,

так и на целые классы уравнений: Bessel,

êê

[ y_p1 = y1, y_p2

= y3, y_p3 = y2 - y1 ], êêy1 = x( t ), y2 = y( t ), y3

y( t )

úú, 0, [ 3, 1, 2] úú

Duffing,

ellipsoidal,

elliptic,

Emden,

erf,

Halm,

Hermite,

Jacobi,

Lagerstrom,

Liouville,

linear_sym,

Ответ дается

виде

списка, состоящего,

свою

очередь, из

списка

Painleve, quadrature, Titchmarsh, Van_der_Pol и др.

уравнений,

где

левой

части

уравнений

использовано

обозначение

производных (в

примере y_p),

списка замен,

начальной

точки и

списка

Пример 1. Проанализируем и решеним уравнение

начальных значений.

d 2 y (x)

(x )

dy (x)

+ y (x )= 0 .

- m 1- y

Порядок ввода параметров для команд построения графиков решения

dx2

(

)

и фазовых портретов следующий: ДУ или система ОДУ, неизвестные

>eq:=diff(y(x),x$2)-mu*(1-y(x)^2)*diff(y(x),x)+y(x)=0;

функции,

диапазон

изменения

независимой

переменной, начальные

æ d2

æ d

условия, необязательные параметры.

eq := ç

y( x ) ÷ - m

( 1 - y( x )

)

y( x ) ÷ + y( x ) = 0

Начальные

условия,

независимо

от того, строится

одна интегральная

èdx

кривая

(фазовая

траектория)

или

несколько,

задаются

списком

в виде

>DEtools[odeadvisor](eq);

[ [ _2nd_order, _missing_x ], _Van_der_Pol ]

«квадратные

скобки

квадратных

скобках». К

необязательным

>dsolve(eq);

параметрам,

кроме

диапазона

изменения

зависимых

переменных,

относятся:

arrows=<…> - тип стрелок векторного поля (SMALL, LARGE, MEDIUM,

LINE); color=<…> - цвет стрелок; linecolor=<…> - цвет линий; method=<…> - метод решения (например, `rkf45`); stepsize=<…> - шаг решения (этот параметр важен, если появляются ломанные).

Команда DEplot из пакета DEtools строит численными методами графики решения или фазовые портреты. Эта команда аналогична команде odeplot, но более функциональна. Она, в отличие отodeplot, сама производит численное решение дифференциального уравнения.

Наиболее часто используемые параметры командыDEplot, кроме перечисленных выше: scene=[x,y] - определяет, какие зависимости выводить на график; iterations=число итераций, необходимое для повышения точности вычислений(по умолчанию это число равно1); stepsize=число , равное расстоянию между точками на графике, по умолчанию оно равно(x2-x1)/20, этот параметр необходим для вывода более гладкой кривой решения; obsrange=true/false - прерывать или

нет вычисления, если график решения выходит за установленный для рисования интервал.

Пример 3.	Нарисовать график решения дифференциального уравнения:
y'''+x y'	+ x2 y = 0 , y(0) = 0 , y'(0) = 1 , y''(0) = 1 в интервале x Î[-4,5] .

>restart; with(DЕtools):

>DEplot(diff(y(x),x$3)+x*sqrt(abs(diff(y(x),x))) +x^2*y(x)=0, {y(x)}, x=-4..5, {[y(0)=0,D(y)(0)=1, (D@@2)(y)(0)=1]}, stepsize=.1, thickness=2);

Для дифференциального уравнения порядка выше первого команда DEplot рисует только кривые решений дифференциальных уравнений,

для систем дифференциальных уравнений первого порядка могут быть нарисованы и фазовые портреты.

С помощью команды DEplot можно построить фазовый портрет в

плоскости (x,			y), для системы двух дифференциальных уравнений:
	dx	= f ( x, y, t),	dy	= g( x, y,t) , если в параметрах данной команды указать

	dt		dt

scene=[x,y].

Фазовый протрет системы двух дифференциальных уравнений первого порядка можно также построить с помощью командыphaseportrait.

Пример 4. Построить фазовый портрет системы дифференциальных

ìx' = y

уравнений: ïí для нескольких наборов начальных условий:

ïy' = x - x3

х(0)=1, у(0)=0.2; х(0)=0, у(0)=1; х(0)=1, у(0)=0.4; х(0)=1, у(0)=0.75; х(0)=0, у(0)=1.5; х(0)=-0.1, у(0)=0.7.

> restart; with(DЕtools):

>DEplot({diff(x(t),t)=y(t),diff(y(t),t)=sin(x(t))},[x( t),y(t)],t=0..4*Pi,[[x(0)=0,y(0)=1],[x(0)=1,y(0)=0.4], [x(0)=0,y(0)=1.5],[x(0)=0,y(0)=0.04],[x(0)=0,y(0)=0.6] ,[x(0)=1,y(0)=0.2],[x(0)=-1,y(0)=0.4],[x(0)=-1, y(0)=0.2]],stepsize=0.1,arrows=none,linecolor=black);

Пример 5. Построить фазовый портрет с полем направлений автономной

системы íìx' = y	для различных начальных условийх(0)=1, у(0)=0;
îy' = sin x

х(0)=-1, у(0)=0; х(0)=p, у(0)=1; х(0)=-p, у(0)=1; х(0)=3p, у(0)=0.2; х(0)=3p, у(0)=1; х(0)=3p, у(0)=1.8; х(0)=-2p, у(0)=1;.

>restart; with(DЕtools):

>DEplot({diff(x(t),t)=y(t),diff(y(t),t)=sin(x(t))}, [x(t),y(t)],t=-1.5*Pi..1.5*Pi, [[0,3*Pi,0.2],[0,3*Pi, 0.7],[0,3*Pi,1.2],[0,Pi,0.2],[0,Pi,0.7],[0,Pi,1.2],[0, -Pi,0.2],[0,-Pi,0.7],[0,-Pi,1.2],[0,-Pi,2],[0,Pi,2], [0,3*Pi,2],[0,-Pi,-1.2],[0,-Pi,-2],[0,Pi,-2],[0,3*Pi,- 2],[0,Pi,2.5],[0,Pi,-2.5]], stepsize=0.1, arrows=none, linecolor=black);

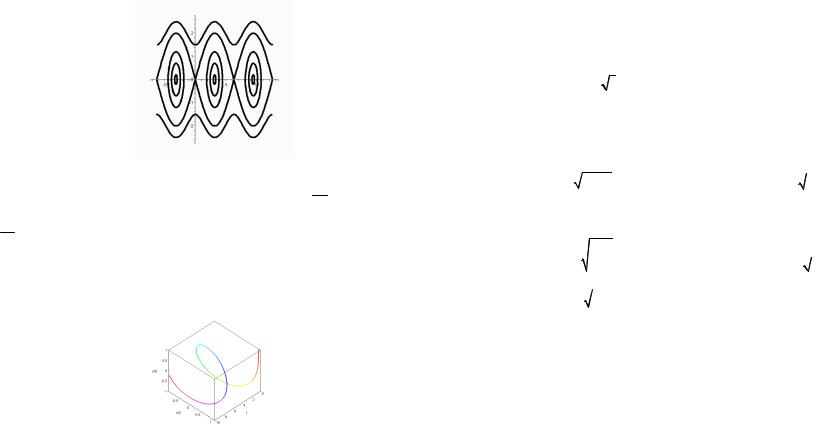
dx ( 2 2 )

Пример 6. Построить решение задачи Коши = y + 1- x - y , dt

dy = -x + (1 - x2 - y2 ), x (0) = 1 , y (0) = 1 . dt

> with(DEtools):DEplot3d({D(x)(t)=y(t)+(1-x(t)^2- y(t)^2)*x(t),D(y)(t)=-x(t)+(1-x(t)^2-y(t)^2)*y(t)}, {x(t),y(t)},t=0..10,[[x(0)=1,y(0)=1]],stepsize=0.1,lin ecolor=t/2);

Лабораторная работа №5

приближенного решений.

№		f (t, y )					t0	y0	№			f (t, y )									t0	y0
							t0	y0													t0	y0
1	t3 cos					y	0	3	2	ln			t ×cos						y		1	0
1	t3 cos						0	3	2	ln			t ×cos								1	0
	5																			3
		-t ×tg				y								ln			t
3						y	0	1	4			sin2						y			1	0

	3
	3																3
																	3
5				ty			2	1	6						ty2						2	1

				t2 - 4									t2 - 4
				t2 - 4									t2 - 4
7				tg t			0	1	8				ye2t								0	1
7				y2			0	1	8				ye2t								0	1
				y2
															t2 y
9		y			1+ t		0	1/e	10						t2 y						0	1/e
					1+ t
					1- t										1+ t
					1- t										1+ t
11							0	0	12		t					2 -t					0	0
		33 y2									t					2 -t
		33 y2									2 y				(1 - t 2)
13			t3 + y				0	3	14		ln		t ×sin							y	1	0
13					t		0	3	14		ln		t ×sin								1	0
					t												3
15					y		0	1	16						y2 t						0	1
15			1 - t2				0	1	16						y2 t						0	1
			1 - t2
17			ye-2t				0	1	18			tye-2t									0	1
19		t 2 ye-2t					0	1	20						tg t						0	1
19		t 2 ye-2t					0	1	20							y					0	1
																y

Решение дифференциальных уравнений и их систем.						- 2 -
Геометрические построения, связанные с ОДУ				Решение систем дифференциальных уравнений
	- 1 -			Найти приближенное	решение в	виде степенного рядаи			численое
Решение дифференциальных уравнений						ìdx		= y (t )	ìx (0 )= 0
						ï
						ï
				решение задачи	Коши для	ï dt			ï	.
Найти приближенное решение в виде степенного ряда до4-го порядка				решение задачи	Коши для	системыí			í	.
						ï	dy	= f (t, x, y)	ïy (0 )= b
		dy				ï			î
		dy	= f (t, y ) при начальном условии			ï
и точное решение задачи Коши:						î dt
и точное решение задачи Коши:		dt				î dt
		dt		Построить на одном рисунке графики двух решений.
y (t0 ) = y0 . Построить на одном рисунке графики точного				и
			87			88

№	f (t, x, y)	a	b	№	f (t, x, y)	a	b
1		0,06	1/7	11		0,01	0,5
2	-aty (t ) - x (t )	0,07	0,125	12		0,02	1/3
3	-aty (t ) - x (t )	0,08	1/9	13		0,03	0,25
4		0,09	0,1	14		0,04	0,2
5		0,1	1/11	15	-ae-0,6 x	0,05	1/6
6		0,01	0,5	16		0,06	1/7
7		0,02	1/3	17		0,07	0,125
8	-ae- x	0,03	0,25	18		0,08	1/9
9		0,04	0,2	19		0,09	0,1
10		0,05	1/6	20	-0, 02e-ax	1,2	0,5

- 3 -

Геометрические построения, связанные с ОДУ

Построить

фазовые

траектории

системы

дифференциальных

уравнений

ì &

ìx = 4 - 4x - 2 y,

íïx = 2x + y -1,

= xy.

ïy& = 6x - y

+1.

îy

ïìx& = 2 + y - x2 ,

ìx& = 1- x2 - y2 ,

= 2x (x - y).

= 2xy.

ïy&

îy

= (x + y )

-1,

= (2x - y)

- 9,

ïx&

= -y2 - x +1.

= (x - 2 y )

ïy&

- 9.

ïy

= x

+ y

- 6x -8 y,

= x

- y,

ïx

= x

(

2 y - x

+ 5

)

2 .

= (x - y )(x - y + 2).

ïy&

ïìx& = x2 + y2 - 5,

10)

ìx& = y2 - 4x2 ,

= (x -1)(x + 3y - 5).

= 4 y -8.

ïy&

îy

ìx& = xy - 4,

11)

íx

= 1- x

- y

12)

íï

= (x - 4)(y - x).

= 4 y -8.

ïy

ìx&

= 2 (x -1)( y - 2),

= (2x - y)

- 9,

13)

14)

ïx

= y2 - x2 .

ïy&

= 9 - (x - 2 y)

ïy&

ìx = 2x + y,

ìx = 2x,

15)

16)

= 3x + 4 y.

= x + y.

îy

ìx& = x - 2 y,

= x

- y,

17)

18)

ïx

= 4x - 3y.

îy

ïy = x - ( y - 2) .

ì &

ìx = 2x - y,

ïx = ln (1- y + y ),

20)

19)

= x.

= 3 -

+ 8y.

îy

ïy

Контрольные вопросы к главе № 5

1.	Какая	команда	позволяет	решить	дифференциальное	уравнение?
	Опишите ее параметры.
2.	С	помощью	каких	операторов	обозначается	производная	в
	дифференциальном уравнении и в начальных условиях?

3.Какой параметр команды dsolve следует установить, чтобы получить фундаментальную систему дифференциальных уравнений?

4.Какой параметр команды dsolve следует установить, чтобы получить

приближенное	решение	дифференциального	уравнения	в	виде
разложения в степенной ряд? Как определяется порядок разложения?

5.Опишите, какие команды нужно ввести, прежде чем построить график приближенного решения, полученного в виде степенного ряда.

6.Какой параметр команды dsolve следует установить, чтобы решить дифференциальное уравнение численно?

7.Как найти значение решения дифференциального уравнения в какойлибо конкретной точке?

8.Какая команда позволяет построить график численно решенного

	дифференциального уравнения?			В	каком	пакете	находится	эта
	команда?
9.	Какой	пакет	предназначен	для	графического		представления		и
	численного решения дифференциального уравнения?
10.	В чем отличие команд odeplot и DEplot?

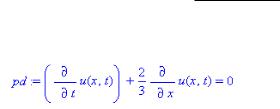
11. Опишите

способы

построения

фазового

портрета

системы Глава 6

дифференциальных уравнений.

Дифференциальные уравнения с частными производными

Решение дифференциальных уравнений с частными

производными

Для решения одного уравнения в частных производных имееются

команда

pdsolve и

набор команд пакетаPDEtools. Обращение

команде pdsolve имеет следующий вид: pdsolve

(PDE, FUN,0PT).

Здесь PDE — дифференциальное уравнение с частными производными,

FUN — неизвестная функция, а ОРТ — дополнительные параметры. Пакет

Maple пытается найти общее решение, используя набор специальных

методов для некоторых видов уравнений и метод разделения переменных в

общем случае. Ответ может быть представлен специальной структурой

PDESolStruc, которая содержит термин &where и состоит из двух полей:

функционального

представления

перечня

обыкновенных

дифференциальных

уравнений, полученных

результате

процедуры

разделения переменных. Решение при этом может быть

получено с

помощью

команды

build

из

пакетаPDEtools.В

качестве

дополнительных параметров ОРТ

могут

использоваться: указание

на

возможную форму решения HINT=HI(HI может принимать значение `+`,

`*` или

алгебраическое выражение), параметр INTEGRATE, означающий

автоматическое интегрирование получающейся системы обыкновенных дифференциальных уравнений, указание на поиск явного решенияbuild. Обратите внимание, что обрамляющие знаки для набора значений`+`, `*` не апострофы, они находятся на клавише с русской буквой Ё.

Пример 1.

>pdsolve(3*diff(g(x,y),x,x)+7*diff(g(x,y),x,y)= x*y, g(x,y) );

g( x, y ) = _F1( y ) + _F2( 3 y - 7 x ) + x3 ( -7 x + 12 y ) 216

Произвольные функции выводятся в виде _F1, _F2.

Пример 2. Рассмотрим линейное однородное уравнение первого порядка:

> pd:=diff(u(x,t),t)+2/3*diff(u(x,t),x)=0;

> sol:=pdsolve(pd);

Полученное общее решение - это «бегущая волна». При помощи команды piecewise организуем начальный профильполусинусоиду и подставим его в решение, попутно образовав функцию для последующего построения графика:

> f1:=x->piecewise(x>0 and x<Pi, 2*sin(x)); f1 := x ® piecewise(0 < x and x < p, 2 sin(x))

> S:=unapply(rhs(eval(sol,_F1=f1)),x,t);

>plot3d(S(x,t),x=-Pi..3/2*Pi, t=0..2*Pi, grid=[30,20], style=hidden, axes=frame, labels= ["x","t","u"], color = black);

Пример 3. Найдем решение уравнения теплопроводности:

> heat:=diff(u(x,t),t)=diff(u(x,t),x,x);

¶	u ( x , t) =	¶ 2
heat :=	u ( x , t) =	u ( x , t)
¶	t	¶ x 2

Попытаемся найти решение в виде произведения:

> pdsolve(heat,HINT = `*`);

Результат содержит неизвестные функции _F1(t) и _F2(t), а также константу _ c1 . Попробуем задать явное представление для решения через функции

Х(х), T(t) и дополнительно укажем, чтобы решение было выписано явно:

> sol:=pdsolve(heat,HINT=X(x)*T(t),build);

(_c1 t)	(	_c	1	x)	_C3 e	(_c1	t)
sol := u(x, t) = _C3 e	_C1 e		1	+	_C3 e		_C2
					(	_c1 x)
					e

Теперь определим параметры и получим частное решение:

> sub:={_c[1]=-4,_C1=I/2,_C2=-1,_C3=1}: S:=simplify (eval (rhs(sol), sub));

S := 1 I e (-4 t + 2 I x) - e (-4 t - 2 I x) 2

Пакет PDEtools

Пакет PDEtools предназначен для преобразования уравнений в частных производных и поиска аналитических решений, кроме того, в его состав входит графическая команда PDEplot.

Некоторые команды пакета PDEtools

Имя	Назначение
	Решение обыкновенных дифференциальных уравнений,
build	полученных		применением			процедуры		разделения
	переменных
casesplit	Представление		дифференциальных			уравнений в			виде
casesplit	подсистем
	подсистем									в
charstrip	Получение	уравнений		характеристик			для	уравнения		в
charstrip	частных производных
	частных производных
dchange	Замена переменных в			уравнениях, кратных интегралах,
dchange	интегро-дифференциальных уравнениях и процедурах
	интегро-дифференциальных уравнениях и процедурах									ее
dcoeffs	Выделение	коэффициентов			при		неизвестной		и	ее
dcoeffs	производных для полиномиального уравнения
	производных для полиномиального уравнения
difforder	Определение порядка частных производных
dsubs	Подстановка выражений для производных
mapde	Преобразование уравнений к другому виду									и
pdetest	Подстановка	в	уравнение		предполагаемого			решения		и
pdetest	вычисление невязки
	вычисление невязки
separabilit	Определение условий, при которых возможно решение
y	уравнения методом разделения переменных
splitsys	Разложение	системы			уравнений		на	независимые
splitsys	подсистемы
	подсистемы
splitstrip	Вычисление характеристик
Для	работы	с	дифференциальными					уравнениями, как
				94

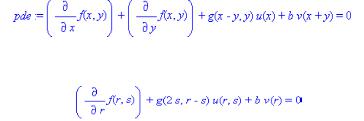
обыкновенными, так и в частных производных, применяются различные преобразования, аппарат теории групп Ли и др. С развитием пакета Maple происходит унификация команд для проведения выкладок и нахождения решений близких по используемому аппарату дифференциальных задач. Так, команда dchange из пакета PDEtools позволяет проводить замену переменных в обыкновенных дифференциальных уравнениях и уравнениях в частных производных, интегралах и интегро-дифференциальных уравнениях, а также замещать глобальные переменные в процедурах. Обращение к команде dchange имеет вид:

dchange(TR,EXPR,NEW,ITR,known,unknown,param,proc)

Обязательными	параметрами являются TR		— множество	соотношений,
определяющих замену переменных, и EXPR — алгебраическое выражение
или процедура,	задающая	уравнение. При	необходимости	указываются:
список имен	новых	переменныхNEW	(если не очевидны новые

переменные), ITR —множество соотношений, определяющих обратную замену. Дополнительными параметрами определяются имена известных функций known, имена функций, которые будут преобразованы, unknown, список имен константparams. Задание этих параметров(known, unknown, params) производится по единой форме, например known =ИМЯ. Здесь ИМЯ — имя или множество имен. Последний параметр рrос определяет процедуру, которая будет использоваться для упрощения полученного выражения.

Пример 1. Рассмотрим пример действия команды dchange по замене переменных в уравнений с частными производными:

>pde:=diff(f(x,y),x)+diff(f(x,y),y)+g(x-y,y)* u(x)+ b* v(x+y)=0;

>tr:={x=r+s,y=r-s}: dchange(tr,pde, known=g, uknown= {u,v});

Построение графиков решений дифференциальных уравнений в частных производных с помощью команды PDEplot

Формат команды PDEplot (PDE,INI,DIA,OPT)

Здесь PDE определяет линейное или нелинейное уравнение

относительно функции, зависящей от n переменных, начальные условия INI даются списком изn+1 элемента и таким образом специфицируют кривую в пространстве размерностиn+1, параметр DIA задает диапазоны для выводимых переменных. При помощи параметра ОРТ формулируются

дополнительные параметры.
	Для вычисления решения(гиперповерхности, проходящей через
кривую,	определенную	параметром INI) используется	метод

характеристик, и система обыкновенных дифференциальных уравнений решается по умолчанию методом Рунге-Кутта четвертого порядка(classical [rk4]). Для решения задачи можно определить другой метод(см. описание методов в разделе, посвященном команде dsolve), однако это может замедлить процесс получения решения.

animate=B00L	Анимация многообразий решения
	(animate=true). По умолчанию при n=2
	действует animate=true и animate=false
	при n>2
basechar=B00t	Режим отображения начального условия
	на плоскость (х,у) при basechar=true. По
	умолчанию принято basechar=false
color=C0L	Цвет решения
ic_assumptions	Заданные в виде равенств или
	неравенств ограничения на начальные
	условия для первых производных
initcolor=COL	Цвет кривой начального условия
iterations=N	Число шагов интегрирования между
	вычисляемыми точками. По умолчанию
	iterations=1
method=MET	Численный метод интегрирования вдоль
	характеристик, см. перечень методов для
	команды dsolve
numchar=N	Число точек для построения
	гиперповерхности решения. Задается в
	виде списка или числа, по умолчанию
	numchar=20
numsteps=[N,M]	Количество вычисляемых точек. По
	умолчанию numsteps=[-10,10]
obsrange=B00L	Прекращение (obsrange=true)
	интегрирования, если отображаемая
	переменная вышла из заданного

	диапазона, и режим безусловного
	расчета при obsrange=false
scene=[x,y.u(x.y)]	Определение осей рисунка
stepsize=VAL	Шаг интегрирования, по умолчанию
	задано максимальное значение stepsize-
	0.25
xi=ximin..ximax.	Определение диапазонов отображения
u(x.y,..)=umin..umax	переменных и функций

Пример. Рассмотрим применение команды PDEplot для изображения ударной волны – решения нелинейного волнового уравнения(уравнения Бюргерса)

> pde:= diff(u(x,t),t)+ u(x,t)*diff(u(x,t),x); ini:= [s,0,.5+.5*sin(s)];dia:=0..4*Pi;

ini := [s, 0, 0.5 + 0.5 sin(s)]

dia := 0 .. 4 p

> PDEtools[PDEplot](pde, x=dia, t=0..3, ini, s=dia, axes=frame, style=hidden, orientation=[-70,15], colour =black, numsteps=12);

Пример решения смешанной задачи для уравнения теплопроводности методом Фурье

Рассмотрим уравнение теплопроводности с начальными и граничными условиями

¶u	- a2	¶2u	= 0, 0 < x < l, t > 0
¶t		¶x2

u (x, 0) = f (x) = x (l - x) , u (0,t ) = 0 , u (l,t ) = 0 .

>PDE:=diff(u(t,x),t)=a^2*diff(u(t,x),x,x);0<x,x<1,t>0;

0 < x, x < 1, 0 < t

> init_c:=u(x,0)=phi(x);

init_c := u(x, 0) = f (x)

> bound_c:=u(0,t)=0,u(1,t)=0;

bound_c := u(0, t) = 0, u(1, t) = 0

> phi:=x->x*(l-x);

f := x ® x (l - x)

Сформулированная задача может быть решена методом разделения переменных

> struc:=pdsolve(PDE,HINT=`*`);

Таким образом, мы получили два обыкновенных дифференциальных уравнения. Введем для них обозначения s1 и s2:

>s1:= diff(_F2(x), `$`(x, 2)) = _c[1]*_F2(x)/a^2; s2:= diff(_F1(t), t) = _c[1]*_F1(t);

s1 := d 2	_F2(x) = _c1 _F2(x)
dx 2	a 2

s2 := d _F1(t) = _c1 _F1(t) dt

Сформулируем теперь соответствующую задачу Штурма—Лиувилля. Мы имеем однородные условия по переменной. Поэтомух рассматриваем уравнение s1, которое после замены постоянной разделения переменных

_ c1 = -l2 удобно записать в виде a2

> eq1:=lhs(s1)+lambda*_F2(x);

Находим общее решение этого уравнения и формируем систему однородных уравнений по граничным условиям:

> _F2:=unapply(rhs(%),x); e1:=_F2(0)=0: e2:=_F2(l)=0: sist:={e1,e2};

_F2 := x ® _C1 sin(		l~ x ) + _C2 cos(			l~ x )
sist := { _C2 = 0, _C1 sin(		l~ l ) + _C2 cos(			l~ l ) = 0 }
Вычисляем определитель этой системы:
> A:=linalg[genmatrix](sist,{_C1,_C2});
é	0		1	ù
A := ê				ú
ê	l~ l )		cos( l~	ú
ësin(	l~ l )		cos( l~	l )û
> Delta:=convert(linalg[det](A),trig);
D := -sin(			l~ l )

Приравниваем определитель нулю — это будет уравнение для определения собственных значений; решаем полученное уравнение и находим собственные значения задачи:

> _EnvAllSolutions:=true:solve(Delta,lambda); p2 _Z5~2

p 2 k 2

В результате мы получили собственные значения l 2 , k Î . Найдем

соответствующие собственные функции:

> ev:=k-> Pi^2*k^2/l^2;

ev := k ® p2 k2 l2

> _F2:=`_F2`: assume(k,posint):subs(lambda=ev(k),eq1);

æ d2

p2 k2

_F2( x )

_F2( x ) ÷

èdx

Напомним,

что

команда

_F2:=`_F2` «отменяет» предыдущее

назначения величины _F2.

Команда assume(k,posint) устанавливает

ограничния

на

значенияk

k ³ 0 ,

что

соответствует множеству целых

чисел.

Нормируем эти функции:

>rhs(%)/sqrt(int(rhs(%)^2,x=0..l));simplify(%,radical, symbolic); ef:=unapply(%,(k,x));

æ p k~ x ö
_C1 sinç		÷	2

ç	l	÷
è		ø

	l _C12
æ p k~ x		ö	2
sinç		÷

ç	l	÷
è		ø

				l
Таким	образом,	найдены		собственные	значения	и	нормированные
собственные функции			задачи	Штурма—Лиувилля найдены. Убедимся в
том, что	l = 0	не	является собственным		значением		рассматриваемой

задачи Штурма—Лиувилля.

> lambda:=0;eq1;

l := 0

dx 2 _F2( x ) = 0

>dsolve(eq1,_F2(x));assign(%);_F2_0:=unapply(_F2(x),x)

_F2( x ) = _C1 x + _C2

_F2_0 := x ® _C1 x + _C2

> eq1_1:=_F2_0(0)=0;eq1_2:=_F2_0(1)=0; eq1_1 := _C2 = 0

eq1_2 := _C1 + _C2 = 0

>A:=linalg[genmatrix]({eq1_1,eq1_2},{_C1,_C2});

>Delta:=convert(linalg[det](A),trig);

é 1		1ù
A := ê		ú
ê	0	ú
ë	0	1û

D := 1

Определитель отличен от нуля, значит существует только тривиальное

решение	и, следовательно,	l = 0	не является	собственным значением
задачи.	Найдем теперь	общее	решение	второго дифференциального

уравнения s2:

> eq2:=lhs(s2)+a^2*ev(k)*_F1(t); dsolve(eq2,_F1(t));

æ d

p2 k~2 _F1( t )

eq2 := ç

_F1( t ) ÷

èdt

t ÷

çç

÷÷

_F1( t ) = _C1 e è

Решение исходной задачи ищем в виде ряда:

>spr:=Sum(C(k)*exp(-ev(k)*a^2*t)*ef(k,x), k= l..infinity);

100

çç

÷÷

æ p k~ x ö

¥ C( k~ ) e

sinç

spr := å

k~ = l

Коэффициенты этого ряда определяем согласно теореме разложения из начальных условий. Введем формулу для коэффициентов Фурье:

>Ck:=Int((phi(x))*ef(k,x),x=0..l);assume(l,posint): Ck:= value(Ck): C:=unapply(Ck,k);

l~	æ p k~ x ö
ó	æ p k~ x ö
ô	x ( l~ - x ) sinç		÷	2
ô	x ( l~ - x ) sinç		÷	2
ô	ç	l~	÷
ô	è	l~	ø
ô					dx
Ck := ô	l~				dx
ô	l~
ô
õ0

C :=k~ ®-	2 l~(5/2)	2 ((-1)k~ -1)
C :=k~ ®-		p3 k~3
		p3 k~3

Формальное решение задачи получено. Преобразуем это решение к другому виду. Индекс k заменим на 2m +1 :

> subs(k=2*m+1,op(1,sol));assume(m,integer):

t ÷

çç

÷÷

æ p k~ x ö

4 l~

( ( -1 )

- 1 ) e

sinç

p3 k~3

>simplify(%):factor(%):solution:=Sum(%,m=0..infinity);

t ÷

ç-

æ p k~ x

ö ÷

4 l~

( ( -1 )

- 1 ) e

sinç

÷ ÷

solution :=

ø ÷

ç-

m~ =

0 è

Запишем окончательное решение задачи в

привычном

математическом

виде

a2p 2 (2m+1)2

æ p

(2m +1)

l 2

sin

x ÷

2 ¥

u (x,t )=

(2m +1)

m =0

Представим полученные решения в виде

двумерного

анимированного

графика:

> with(plots):a:=1;l:=12;

u(t,x):=sum(8*l^2/Pi^3/(2*m+1)^3*exp(-a^2*Pi^2* (2*m+1)^2 /l^2*t) * sin(Pi*(2*m+1)/l*x), m=0..1000): animate(plot,[u(t,x),x=0..12, y=-1..40], t=0.0001..30, frames=30,thickness=3);

a := 1

l := 12

Лабораторная работа №6

Применение метода разделения переменных

Задача

колебаниях

струны, закрепленной на

концах,

сводится к

решению

уравнения

¶2u

= a

¶2u

при

начальных и

¶t2

¶x2

граничных условиях

¶u

= u

x ,

= u

x , u

= 0, u

= 0

t =0

0 (

)

¶t

1 (

)

x =0

x =l

t =0

Решить задачу о колебании струны 0 < x < l

с закрепленными

концами в предположении, что внешние силы отсутствуют, если

1) начальные скорости точек струны равны

,нулюа начальное

отклонение u0 имеет форму синусоиды u0 (x )= Asin

p nx

n Î .

2)начальные скорости точек струны равны ,нулюа начальное отклонение u0 имеет форму параболы, осью симметрии которой служит прямая x = l / 2 , а вершиной – точка M (l / 2, h) .

101

102

3) в начальном		положении			струна		находится в		покое( u = 0 ), а
начальная скорость u1 (x) = v0					= const, x Î[0,l]				0
начальная скорость u1 (x) = v0					= const, x Î[0,l]
4) в начальном положении струна находится в покое ( u0									= 0 ), а
начальная скорость						], где 0 £ a < b £ l
ìv	= const, если x Î			a, b
u1 (x )= íï 0		[
ï0,	если x Ï[a, b ]
î
5) в начальном положении струна находится в покое ( u0									= 0 ), а
начальная скорость
ì		p (x - x0 )
ïA cos			, если x Î[x0				-a, x0 +a ]	, где	0 £ x0 -a <
ïA cos			, если x Î[x0				-a, x0 +a ]		0 £ x0 -a <
u1 (x )= í		2a							< x0 +a £ l
ï	если x Ï[x0 -a, x0 +a ]								< x0 +a £ l
î0,	если x Ï[x0 -a, x0 +a ]

Решить задачу о продольных колебаниях однородного стержня при произвольных начальных данных в каждом из следующих случаев:

6) один конец стержня( x = 0 ) жестко закреплен, а другой конец ( x = l ) свободен

7) оба конца стержня свободны

8) один конец стержня( x = 0 ) закреплен упруго, а другой конец ( x = l ) свободен

Задача о распространении тепла в тонком однородном стержне

0 < x < l , боковая поверхность которого теплоизолирована, а концы x = 0 и x = l поддерживаются при нулевой температуре, приводится к

решению уравнения теплопроводности

¶u

= a2

¶2u

при

начальных и

¶t

= u0 (x), u

¶x2

граничных условиях u

t =0

x =0

= 0,

x =l = 0 .

Дан

тонкий

однородный

0 < x < l

, боковая

стержень

поверхность

которого

теплоизолирована. Найти

распределение

температуры u (x,t ) в стержне, если

9) концы

стержня

x = 0 и x = l

поддерживаются

при нулевой

температуре, а начальная температура u

t =0 = A = const

103

10)

концы

стержня

x = 0

x = l

поддерживаются

при нулевой

температуре, а начальная температура u

t =0

= Ax (l - x),

A = const

11)

конец x = 0

поддерживается при нулевой температуре, а на конце

x = l

происходит

теплообмен

с окружающей

средой

нулевой

температуры. Начальная температура стержня u

t =0 = u0 (x)

12)

на обоих концах стержня( x = 0 и x = l ) происходит теплообмен с

окружающей

средой,

начальная

температура

стержня

t =0 = u0 (x)

13)

концы

стержня

x = 0

x = l

теплоизолированы,

начальная

температура u

t =0

= u0

= const

14)

концы

стержня

x = 0

x = l

теплоизолированы,

начальное

распределение температуры задается формулой

ìu

= const, если 0

< x < l / 2

= í

t =0

î0, если l / 2 < x < l

15)

концы стержня теплоизолированы, а

если 0 < x < l / 2

, где u0 = const

t =0

2u0

(l - x), если l / 2 £ x < l

Решить следующие смешанные задачи:

= x2

16)

= u

, 0 < x < 1

, u

= 0 ,

t =0

-1

17)

uxx

= ut

+ u , 0 < x < l ,

x =0

= u

x =l

= 0 , ,

t =0

= 1

= x2

18)

= u

- 4u ,

0 < x < p

, u

x =0

= u

= 0 , ,

t =0

-p x

< x < l

Дан

тонкий

однородный

боковая

стржень

поверхность

которого

теплоизолирована. Найти

распределение

температуры u (x,t ) в стержне, если

19)

концы

стержня

x = 0

x = l

поддерживаются

при

постоянных

температурах

x =0

= u1 ,

x =l

= u2 ,

начальная

температура

t =0

= A = const

20)

концы

стержня

x = 0

x = l

имеют

постоянную

температуру

x =0

= u

x =l = u1 ,

начальная

температура

задается формулой

t =0

= u0 (x) = Ax (l - x) , где

A = const

104

Глава 7

Процедуры

В этой главе подробно рассмотрим работу с процедурами вMaple.
Сразу необходимо подчеркнуть следующий момент: программирование в
Maple отличается		от	программирования	на	стандартных	языках
программирования в силу аналитических"способностей" Maple. Поясним
сказанное:
Пример 1.	Разработать		процедуру, вычисляющую абсолютное значение
некоторой	величины.	Вероятнее всего мы		получим следующий		вид
процедуры:

>ABS:=proc(x)

if x<0 then -x else x end if; end proc;

ABS := proc(x) if x < 0 then -x else x end if; end proc;

Эта процедура будет давать хорошие результаты в случае передачи ей в качестве параметра вещественных числовых значений. Но как только ей в качестве параметра будет передана переменная, которой не присвоено никакого числового значения, а такое в Maple может произойти, то наша процедура выдаст сообщение об ошибке:

> ABS (b) ;

Error, (in ABS) cannot determine if this expression is true or false: b < 0

Действительно, невозможно определить, будет ли переменнаяb меньше или больше нуля. Поэтому переработаем содержимое процедуры таким образом, чтобы она в подобных случаях возвращала невычисленное значение нашей функции ABS ():

>ABS:=proc(x)

if type(x,numeric) then

if x<0 then -x else x end if; else 'ABS'(x) end if; end proc:

>ABS (b) ;

		ABS(b)
	Определение и вызов процедур
Определение		процедуры Maple имеет	следующий	общий
синтаксис:
рrос	( [ список_формальных_параметров ] )
[ local список_локальных_переменных; ]
[ global список_глобальных_переменных; ]
105		106

[ options список_опций; ]
[ description строка_описания; ]
последовательность_операторов
end proc
При	объявлении	процедуры	единственным	обязательным
параметром является последовательность операторов, формирующих тело
процедуры. Остальные параметры, определяющие локальные и глобальные
переменные,	список формальных параметров, задающие специальные
опции режима выполнения процедуры и строку описания, могут полностью
отсутствовать.
Обычно возвращаемым значением процедуры является значение
последнего вычисленного в теле процедуры оператора.
При	вызове процедур следует		помнить, что Maple	сначала

вычисляет все фактические параметры, а затем уже использует полученные значения в качестве параметров процедуры:

> vector_length:=proc(x,y) sqrt(x^2+y^2); end proc; vector_length:= proc(x, y) sqrt(x^2 + y^2) end proc;

> z:=sqrt(y);

z := y

> y:=x;

y := x

> x:=a;

x := a

> vector_length(z,y);

a + a 2

Если в процедуре задан только один параметр, то при таком способе задания круглые скобки можно опустить:

> g:=x->if x<0 then -1 elif x=0 then 0 else 1 end if; g := x ® if x < 0 then -1 elif x = 0 then 0 else 1 end if;

> g(-9),g(0),g(9);

-1, 0, 1

107

Определения		процедур	трактуютсяMaple	как	правильные
выражения, поэтому их можно создавать и вызывать и без присваивания
имен:
> ((x,y)->sqrt(x^2+y^2))(4,a);
		16 + a 2
> proc(x,y)	sqrt(x^2+y^2);		end proc	(c,d);
		c 2 + d 2
Однако	неименованные		процедуры	обычно	используются
совместно с функцией map ():
> map(x->x^3,{1,5,9,4});
		{1, 64, 125, 729}

Передача параметров

При вызове процедуры Maple сначала вычисляет ее имя, а затем последовательность переданных ей параметров, причем если значением какого-либо параметра оказывается последовательность, то формируется одна результирующая последовательность величин, которая и трактуется как последовательность фактических параметров:

> s:=a,b,c; t:=2;

s:= a, b, c t := 2

>M:=(x,y,z,e)->x*y*z*e; M(s,t);

M := (x, y, z, e) ® x y z e

2 a b c

Количество	фактических	параметров	не обязательно должно
равняться количеству	формальных	параметров	процедуры, определенных

при ее объявлении. Если их меньше, то ошибка во время выполнения процедуры возникнет только тогда, когда при вычислении тела процедуры действительно потребуется значение этого отсутствующего параметра. Если фактических параметров больше, чем формальных, то никакой ошибки не будет сгенерировано — дополнительные параметры будут просто проигнорированы.

108

> mXYZ:=proc(x,y,z) if x>y then x else z end if end proc;

mXYZ := proc(x, y, z) if y < x then x else z end if; end proc;

> mXYZ(1,2,3,4,5,6);

> mXYZ(5,1);

> mXYZ(l,5) ;

Error, (in mXYZ) cannot determine if this expression is true or false: 5 < l

Первый вызов процедуры mXYZ с большим числом фактических параметров выполнился нормально. Второй вызов этой же функции с двумя параметрами тоже завершился нормально, так как значение третьего параметра не потребовалось. А вот третий вызов с двумя параметрами завершился сообщением об ошибке, что необходим третий параметр, который в вызове отсутствует.

Чтобы избежать ошибок в процедурах, работающих с определенным типом параметров, следует при объявлении процедуры объявлять и тип ее параметров. Для этих целей предназначена операция проверки типа ::, первым операндом которой является имя формального параметра, а вторым его тип:

> mXYZ:=proc(x::numeric,y::numeric,z) if x>y then x else z end if end proc;

mXYZ := proc(x::numeric, y::numeric, z) if y < x then x else z end if; end proc;

В этом случае, прежде чем начнется выполнение операторов тела

процедуры,	Maple	проверит	вычисленные	значения	фактических
параметров соответствующим в объявлении процедуры типам формальных
параметров.	Если	какой-нибудь	параметр	не будет	соответствовать

заданному типу, то отобразится сообщение о несоответствии параметра объявленному типу:

> mXYZ(5,'y',z);

Error, invalid input: mXYZ expects its 2nd argument, y, to be of type numeric, but received y

При проверке типа передаваемого в процедуру параметра можно использовать все основные типыMaple, структурные типы и типы, созданные пользователем.

109

При объявлении процедуры не обязательно задавать имена формальных параметров. Язык Maple предоставляет специальное имя args,

с помощью которого можно получить доступ к любому переданному в процедуру фактическому параметру. Значением переменной args является последовательность всех фактических параметров, а получить значение i-ro параметра можно, воспользовавшись индексной записьюargs[i]. Общее количество переданных при вызове процедуры фактических параметров хранится в специальной переменнойnargs. Это позволяет легко писать процедуры с произвольным количеством фактических параметров.

Пример 2. Написать процедуру, вычисляющую максимальное значение числовой последовательности с произвольным числом параметров

> MAX:=proc()

if nargs=0 then -infinity elif nargs=1 then args[1];else m:=args[1];

for i from 2 to nargs do

if args[i-1]<args[i] then args[i] else args[i-1] end if;

end do; end if; end proc:

Warning, `m` is implicitly declared local to procedure `MAX`

Warning, `i` is implicitly declared local to procedure `MAX`

> MAX(45/46,56/57, 97/99);

Необходимо включить в тело процедуры проверку членов рассматриваемой последовательности на соответствие допустимым типам. Понятно, что в нашем случае все фактические параметры должны быть числовыми (numeric), поэтому следующий оператор, поставленный самым первым оператором в теле процедуры, исправит это упущение:

for i in args do

if not type(i,numeric) then

error "Parameter " || i || " must be numeric" end if end do;

В этом операторе цикла для завершения процедуры использован оператор error, который генерирует исключительное состояние ошибки, печатает сообщение, переданное ему в качестве параметра, и останавливает выполнение процедуры. Теперь исправленный вариант нашей процедуры

110

при обращении к ней с нечисловыми фактическими параметрами будет печатать сообщение о несоответствии параметра числовому типу:

> MAX(8/9,56/57,x,97/99);

Error, (in MAX) Parameter x must be numeric

Локальные и глобальные переменные

В процедурах Maple существуют локальные и глобальные -пе ременные. Они определяются при описании процедуры после ключевых


слов global	и local. Локальные		переменные видимы только в пределах
процедуры, глобальные переменные видимы в любом месте рабочего листа.
Рекомендуется		все	переменные, используемые	процедурой,
описывать	в секцияхlocal и		global. Если тип переменных явно не

определен, то существует правило определения типа переменной:

•если переменной внутри процедуры присвоено какое-либо значение, то эта переменная считается локальной;

•переменные, используемые в циклеfor или как индексная переменная в командах seq ( ), add ( ) или mul ( ), также считаются локальными.

Остальные переменные считаются глобальными.

Для понимания работы с глобальными и локальными переменными внимательно изучим следующий пример процедурыGL и

результаты ее выполнения.

Пример 2.

>GL:=proc()

>local l,x,y; global g;

>g:=x^2;l:=x^2;x:=y^2; y:=2;print(g);print(l); end proc;

GL := proc( ) local l, x, y; globalg;

g := x ^ 2; l := x ^ 2;

x:= y ^ 2;

y:= 2; print ( g ) ; print ( l )

end proc

> GL();

111

112

> g; l;

16 l

Вызов этой процедуры показывает, что глобальная переменная вычислена полностью (ее значение равно числу16), тогда как локальная переменная только до первого уровня (ее значение равно x2 ). Переменная g действительно имеет значение, которое она получила во время выполнения процедуры GL(), а переменная l, не связанная с локальной переменной с таким же именем в процедуре GL() , не имеет никакого значения, и поэтому вычисляется равной своему имени.

Параметры описания процедур

Параметры описания процедур записываются в секцииoptions. Параметры приведены в таблице.

ПАРАМЕТРЫ	ОПИСАНИЕ
remember	определяет таблицу памяти для процедуры
builtin	определяет процедуру как “встроенную”
system	определяет “системную” процедуру
operator	объявляет процедуру - функциональный оператор

arrow	уточнение опции operator (стрелочная нотация)
trace	отлаживаемая процедура
package	определяет пакетную процедуру
Copyright	защита от просмотра текста процедуры

Параметр remember определяет, что все результаты обращений к процедуре будут заноситься в таблицу памяти процедуры.

Пример 3. Рассмотрим процедуру, вычисляющей числа Фибоначчи:

>F:=proc(n::integer)

>if n<2 then n else F(n):=F(n-1)+F(n-2) end if end proc: F(300);

2222322446294204455297398934619099672066669390964997

64990979600

> time(F(3000));

0.031

Если добавить в тело процедурыoptions remember;то время, затраченное на ее выполнение, уменьшается:

> time(F(3000));

0.007

113

Возвращаемые значения

Любая процедура Maple возвращает единственное значение, которым обычно является значение последнего выполненного в теле процедуры оператора. Однако это не единственный способ передачи вычисленных в теле процедуры величин. Как и в других языках программирования, процедура Maple может возвращать значения через свои параметры, но этот способ несколько отличается от аналогичного в других языках программирования.

Для того чтобы процедура возвращала некоторое значение через параметр, необходимо в теле процедуры этому параметру присвоить требуемое значение. Процедура следующего примера возвращает true, если символ, определяемый первым параметром, содержится в строке второго параметра, в противном случае— false. Третий параметр возвращает позицию первого вхождения заданного символа в строку.

Пример 4. Возврат значений через параметр процедуры

>restart;f:=proc(x::string, s::string, n::name) local i,j; j:=0; for i in s do

j:=j+l;

if x=i then n:=j; return true; else false; end if; end do; end proc:

>f("1","1234",n);

true

> n;

> f("4","1234",n);

Error, invalid input: f expects its 3rd argument, n, to be of type name, but received 1

Процедура последовательно в циклеfor проверяет равенство переданного ей символа с каждым символом строки. В случае совпадения параметру n присваивается номер позиции этого символа в строке и процедура завершается выполнением оператора return.

Первое обращение к процедуреf() завершается совершенно правильно, а переменная n содержит правильный номер позиции символа "i" в строке "1234". Однако второй вызов этой же процедуры с параметром n приводит к ошибке. Дело в том, что после первого вызова переменнаяn

получает значение 1 и ее тип становится	равнымinteger, а	не name,	как
этого требует процедура. Для выхода из	этой ситуации	в нашем	случае
114

следует передавать в процедуру переменную n не вычисленной, заключая ее в одинарные кавычки или выполняя команду evaln ( ):

> f("4","1234",evaln(n));n;

true

> f("2","1234",'n');n;

true

Замечание Процедура примера будет корректно работать, если при


каждом	ее	вызове	в	качестве	третьего	параметра		передавать
переменную, которой не присвоено никакого значения.
Более		корректный		способ	исправления		подобной		ошибки
заключается в использовании типаevaln при определении формального
параметра	процедуры, через			который	будет	возвращаться		некоторое
значение. Этот тип Maple, используемый исключительно при задании типов
параметров процедур, предписывает вычислять действительный параметр
процедуры	только до		уровня имени. В		теле	процедуры		его	можно

использовать обычным способом. Измененная процедура предыдущего примера представлена в следующем примере.

Пример 5. Возврат значений через параметры с использованием типа evaln > f:=proc(x::string, s::string, n::evaln)

local i,j; j:=0;

for i in s do j:=j+1;

if x=i then n:=j; return true; else false; end if; end do; end proc: f("x","12x34",n);n;

true

> f("4","12x34",n);n;

true

Еще одним отличием использования параметров	в процедурах
Maple является то, что фактические параметры вычисляются	только один

раз при входе в процедуру, поэтому их нельзя свободно использовать в теле процедуры, как локальные параметры: если формальному параметру в теле процедуры присвоено какое-то значение, то при дальнейшей ссылке на этот параметр мы не получим присвоенного значения. Единственное законное присваивание возможно только в случае возвращения значения через этот параметр. Процедура simple следующего примера проиллюстрирует это явление. Формальный параметр х определен как типevaln(integer). Это означает, что соответствующий ему фактический параметр при входе в процедуру должен вычисляться до уровня имени переменной, которая хранит целое значение. В теле процедуры, так как параметр х является именем, чтобы использовать его значение, приходится явно прибегать к функции eval( ) . В первом операторе изменяется значение формального

ей параметра, а сам формальный параметр является возвращаемым значением процедуры simple(). Казалось бы, если мы передадим в процедуру переменную со значением, например 5, то результатом выполнения процедуры должно быть значение6. Однако ее вызов с указанным параметром показывает, что значением процедуры является имя, ха не число 6. Здесь работает правилоMaple вычисления фактических параметров один раз, а наш параметр как раз и должен вычисляться до своего имени. А вот значение самого параметра увеличилось на единицу, так как он был изменен в теле процедуры.

Пример 6. Использование значений параметров в тепе процедуры

>simple:=proc(x::evaln(integer))

x:=eval(x)+1;

х;

end proc:

>x:=6;

x:= 6

>simple(x);

> x;

		7
Правило	использования	фактических	параметров : таково
присваивать им возвращаемые значения можно только непосредственно
перед выходом из процедуры. Если необходимо, например, в цикле менять
значение параметра, то следует его первоначальное вычисленное значение
присвоить локальной переменной,		произвести вычисления, а затем

присвоить формальному параметру полученный результат.

115

116

Прекратить		выполнение процедуры и	возвратить некоторое
требуемое значение можно в любом месте тела процедуры. Для этих целей
применяется	оператор return. Значение следующего		за ним выражения и
является воз вращаемым значением. Мы использовали данный оператор в
одном из	примеров,	когда определяли первое	вхождение символа в

заданную строку, а возвращаемым значением была позиция этого символа в строке. Общий синтаксис этого оператора следующий:

return выражение

Выражение может быть любой структурой данных, включая последовательность, список и множество. Оно может и отсутствовать, в этом случае процедура ничего не возвращает.

Кроме возврата значений процедура может возвратить ошибку, сгенерировав исключительную ситуацию, создающую специальный объект исключительного состояния, который в дальнейшем можно использовать в конструкции try для анализа возникшей ошибки и выполнения определенных корректирующих действий.

Возврат ошибки из процедуры осуществляется операторомerror, который создает объект исключительного состояния, печатает сообщение об ошибке и немедленно прекращает выполнение процедуры:

error строка_сообщения [, список_параметры]
Строка	сообщения — это	строка,	которая	участвует	в
формировании общего сообщения об ошибке в				процедуре	после ее
завершения оператором error. Если в ней заданы специальные переменные,
начинающиеся с символа процента (%), за которым следует целое число без
знака или	со знаком минус, то вместо		нее в	строку сообщений
подставляется	значение переменной	из	списка	параметров, причем

абсолютное значение целого числа соответствует порядковому номеру переменной в списке. В случае целого числа со знаком минус значение соответствующего параметра преобразуется в порядковое числительное(с точки зрения английского языка) и подставляется в строку сообщений (естественно, оно должно быть целым). Пример формирования строки сообщений показан ниже:

> n:=6:

error "%-l parameter has the value %2", 2, n;

Error, %-l parameter has the value 6

Специальный параметр %0 будет отображать через запятую и пробел все значения переменных из списка параметров:

> error "All parameters: %0", 2,n;

Error, All parameters: 2, 6

Создаваемый оператором error объект исключительного состояния представляет последовательность выражений со следующими элементами:

□имя процедуры, в которой было сгенерировано исключительное состояние, или константа , оесли исключительное состояние было сгенерировано на верхнем уровне, а не в процедуре;

□строка сообщения;

□список параметров в случае его задания.

Созданный объект исключительного состояния присваивается глобальной переменной lastexeption в виде последовательности выражений,

а также для совместимости с предыдущими версиямиMaple глобальной переменной lasterror присваиваются фактические параметры оператора error.

Сообщение об ошибке печатается в виде:

Error, (in имя_процедуры) текст_сообщения
Текст	сообщения			представляет		строку			сообщений	с
подставленными в нее значениями переменных, заданных в списке
параметров оператора error. Если				процедура не		имеет имени, то вместо
имени процедуры печатается"unknown", если ошибка сгенерирована на
верхнем уровне,	то часть сообщения в круглых скобках								вообще не
печатается, как было в наших двух предыдущих примерах выполнения
оператора error.
В процедуре можно "поймать" ошибку с помощью конструкции try-
catch, заключив	в нее блок операторов,					котором		может быть
сгенерирована ошибка. Она имеет следующий синтаксис:
try блок проверяемых_операторов
catch строка_ошибки : блок_операторов
[ finally блок_завершающих_операторов ] end try
Когда	вычисление		доходит		до	блокаtry,	то	начинается
последовательное	выполнение			операторов		из	блока		проверяемых
операторов. Если в результате их выполнения не сгенерировано никакой
ошибки, то выполняются операторы завершающего блокаfinally, если он
задан, иначе управление передается оператору, следующему за оператором
end try.
Если	при	выполнении			проверяемых			операторов		будет
сгенерирована	ошибка,	то	их	дальнейшее		выполнение			немедленно

прекращается, а строка сообщения созданного объекта исключительного состояния сравнивается со строкой ошибки во всех операторахcatch блока try. Если соответствие найдено, то выполняется соответствующий блок операторов, заданный после двоеточия (:) в соответствующем блоке catch.

117

118

Если соответствия не найдено, то выполняются операторы блока finally, а исключительное состояние регенерируется вне блока try.

В блоке catch через запятую может быть задано несколько строк ошибок, тогда операторы этого блока выполняются при возникновении любой из перечисленных ошибок. Если строка ошибки вообще отсутствует,

то такой блок catch "ловит" все возникающие при выполнении проверяемых операторов ошибки.

119

Глава 8

Взаимодействие Maple с другими программами

Генерация кодов Maple в С и Фортран

Пакет codegen предназначен для оптимизации текстов программ на языке Maple и перевода Maple-выражений в конструкции языков программирования. Рассмотрим некоторые команды работы Mapleс - выражениями и их перевод на такие языки программирования— С и Фортран. Перед обращением к пакету его нужно подключить командой

with(codegen).
Перечислим	некоторые	команды	из	codegen,пакета

предназначенные для модернизации текстов Maple-процедур и выражений:

makeproc(a, х)	переводит выражение а(или переменную типаlist,
	состоящую из выражений) в процедуру с параметром х
	(или набором параметров);
makeparam(x, f)	преобразует	переменную ,	хвходящую	в Maple-
	процедуру f, во входной параметр;
makeglobal(x, f)	преобразует	переменную ,	хвходящую	в Maple-
	процедуру f, в глобальную переменную;
declare(x::t, f)	описывает переменную х, входящую в Maple-процедуру
	f, как переменную типа t;
makevoid(f)	преобразует Maple-процедуру с именем f в процедуру
	без возвращаемого значения;
optimize(expr)	оптимизирует Maple-выражение expr. В качестве expr
	может выступать алгебраическое выражение, массив,
	набор уравнений или процедура;
prep2trans(f)	преобразует процедуру f к виду, удобному для перевода
	на алгоритмические языки. В частности,			кусочно-
	непрерывныая	функция (piecewise) представляется как
	условный оператор, а сумма (Sum) — как цикл;
cost(expr)	оценивает число элементарных операций, необходимых
	для выполнения выражения ехрг.

Пример 1. Рассмотрим пример работы командыprep2trans. Определим функцию f, которая вычисляет интеграл функции sin(ax) на интервале от 0 до p по формуле Симпсона. Для этого воспользуемся командойSimpson

пакета student и командой makeproc. > with(codegen):

120

f:=makeproc(student[simpson](sin(a*x),x=0..Pi,10), a::float);

Warning, the protected name MathML has been redefined and unprotected

f := proc(a::float)

1/30´p´( sin( a´p) + 4´Sum( sin( 1/10´a´( 2´i - 1 )´p), i = 1 .. 5 ) + 2´Sum( sin( 1/5´a´i´p), i = 1 .. 4 ) )

end proc

> prep2trans(f); proc(a::float)

local i1, i2, s1, s2, t1, t2; s1 := 0;

for i1 to 5 do s1 := s1 + sin( 1/10´a´( 2´i1 - 1 )´p) end do ;

s2 := 0;

for i2 to 4 do s2 := s2 + sin( 1/5´a´i2´p) end do ; 1/30´p´( sin( a´p) + 4´s1 + 2´s2 )

end proc

Обратим внимание на то, что все суммы в результате действия команды prep2trans были преобразованы в операторы циклов.

Описанные процедуры часто используются для приведенияMaple- выражений к виду, удобному для преобразования в программы на языках программирования. Перейдем теперь непосредственно к командам перевода Maple-выражений на алгоритмические языки.

Вывод выражения в виде Фортран-операторов осуществляется по команде fortran(expr, options)

Здесь в качестве rехрмогут выступать выражение, массив выражений, процедура или список уравнений. Параметры options могут принимать следующие значения: filename="name.ext" (результат выводится в файл), optimized (Фортран-выражения оптимизируются, вводятся вспомогательные переменные), digits и mode (задание точности вычислений).

Чтобы записать выражение на языке ,Снеобходимо пользоваться командой C(expr,options)

Параметры этой команды аналогичны параметрам, описанным для команды fortran.

Пример 2. Приведем примеры использования этих двух команд. Сначала определим выражение f, а затем переведем его на С и Фортран:

> f:=a+b^5*sin(b^3);

f := a + b5 sin( b3 )

> C(f);

t0 = a+b*b*b*b*b*sin(b*b*b);

> fortran(f);

t0 = a+b**5*sin(b**3)

Теперь обратимся	к команде С с параметром оптимизации текста
выражения:
> C(f, optimized);
t1	= b*b;
t2	= t1*t1;
t5	= sin(t1*b);
t7	= a+t2bt5;

Для	оптимизации	выражения	введены	дополнительные
переменные, которые необходимо описывать вручную в программе на. С
Это не так сложно в случае небольших формул , но может стать очень
трудоемким для громоздких выражений, Для избежания ручного труда
преобразуем	выражение в	процедуру с	двумя параметрами и снова

обратимся к команде С:

> g :=proc(a::float,b::float) a+b^5*sin(b^3) end proc;

g:= proc(a::float, b::float) a + b^5´sin( b^3 ) end proc

>C(g, optimized);

#include <math.h> double g(a,b) double a;

double b;

{

double t1; double t2; double t5;

{

t1 = b*b;

t2 = t1*t1;

t5 = sin(t1*b); return(a+t2*b*t5);

}

121

122

В результате получился текст процедуры	на языке, не С
требующий никакой дополнительной работы.
Пример 3. Приведем пример использования команды	генерации кодов
языка Фортран с сохранением текста результата в файл:

>fortran(g,optimized,filename="res.for");

Врезультате выполнения команды будет создан файлres. for со следующим текстом:

doubleprecision function g(a,b) doubleprecision a doubleprecision b

doubleprecision t1 doubleprecision t2 doubleprecision t5

t1 = b**2

t2 = t1**2

t5 = sin(t1*b) g = a+t2*b*t5 return

end

Начиная с версии Maple 6.0 появилась возможность подключения внешних процедур, написанных на алгоритмических языках. Для описания и вызова внешних процедур используются соответственно команды

define_external и call_extarnal. В документации по пакету и в справочной системе дано описание этих команд и приведен пример процедуры. При вызове внешних процедур важно согласование типов данныхMaple и языков программирования, соответствие которых изложено в руководстве по пакету. Отметим, что по умолчаниюMaple использует транслятор Microsoft С для операционной системыWindows. Таким образом, процедуры, написанные на С(или другом языке, поддерживающем интерфейс С), и находящиеся в библиотеках (DLL в среде Windows), могут теперь подключаться кMaple динамически и вызываться как команды

Maple.

Преобразование документов Maple в форматы LaTeX, RTF, HTML

В этом разделе мы рассмотрим взаимодействиеMaple с системами подготовки научных публикаций, как традиционных, так и электронных. Замечательная способность Maple представлять математические результаты

в форматах, стандартных для систем публикаций, используется уже давно.

Maple позволяет	автоматически					переводить		рисунки	и	формулы,
полученные в результате громоздких вычислений, в нужный формат без
дополнительной ручной обработки. В настоящее время система верстки
LaTeX фактически является стандартом для научных публикаций. В LaTeX
существует свой язык для написания формул.
Для перевода математического выражения ехрr в формат системы
редактирования LaTeX в		Maple		используется команда latex(ехрг)						или
latex(expr."name.ext")
Во втором варианте результат работы команды выводится в файл.
Полученные выражения можно легко вставлять LaTeXв -документы, но
следует помнить, что полученную формулу необходимо включить в нужное
окружение (например, в		символы $				для	формул	внутри	текста или
конструкции \begin{equation}... \end{equation}							для выделенных		в	строку
формул). Рассмотрим следующий пример:
Пример 4. Обращение к команде latex:
> Int(1/(x^2+1), х) = int(1/(x^2+1), x);
		ó		1
		ô		1	dõ = arctan ( x )
		ô
		ô	2
		ô	2	+ 1
		ôx		+ 1
		õ

> latex(%);

\int \! \left( {x}^{2}+1 \right) ^{-1}{d\mbox {{\tt `х`}}}=\arctan\left( x \right)

В LaTeX-документе эта формула при ее размещении в отдельной строке должна выглядеть следующим образом:

\begin{equation}

\int \! \left( {x}^{2}+1 \right) ^{-1}{d\mbox {{\tt `х`}}}=\arctan \left( x \right)

\end{equation)

Обратим внимание на то, что результат преобразования выражения

отличается от вида	выражения Mapleв -документе, так		как здесь
используется отрицательная степень, а не дробь. Таким образом, любое
математическое выражение можно преобразовать в формат LaTeX.
В Maple существует возможность перевода		в различные форматы
всего Maple-документа.	Преобразовать рабочий	документ	можно из

основного меню Maple, выбрав пункт File, а затем Export As или Save As. После этого надо выбрать требуемый формат документа при помощи дополнительного меню. Список возможных форматов дан в таблице.

ТИП ДОКУМЕНТА	ОПИСАНИЕ
Maple text	Текстовый формат с записью математических

123

124

выражений на языке Maple

Format). Эта

возможность позволяет

использоватьMaple и

как

среду

Plain text

Текстовый

формат

имитацией

автоматической

разработки

математических

электронных

публикаций.

математических выражений

Поскольку последние версии Microsoft Word поддерживают HTML-формат,

Maple explorer

Формат, близкий к формату LaTeX

то

это

предоставляет

еще

одну

возможность

автоматического

LaTeX

LaTeX-документ

преобразования

Maple-документов

текстовые

документыWord.

RTF (Rich text format)

Расширенный текстовый формат

результате преобразования по умолчанию создается основной файл с

расширением .html и именем, совпадающим с именемMaple-документа,

HTML

Гипертекстовый формат

При преобразовании Maple-документа

в LaTeX

все

рисунки

который должен загружаться программами, поддерживающими фреймы,

например Netscape или Microsoft Explorer. Кроме

того,

создается

ряд

автоматически

преобразуются

форматEncapsulate

PostScript,

дополнительных HTML-файлов и файлы с рисунками, причем все формулы

математические

выражения

переводятся

на язык формул пакетаLaTeX.

рисунки преобразуются в растровые графические файлы форматаGIF.

Рисунки сохраняются в файлах с именами, состоящими из имени документа

Все эти файлы имеют имена

номерами. В основном файле

содержатся

и номера

рисунка. При

записи формул Maple использует свои команды и

ссылки на дополнительные HTML-файлы. Перед конвертацией появляется

окружения, которые реализованы в пакете дляLaTeX mapl e2e. Стилевые

диалоговое

окно, в котором

предлагается

выбрать

имя

каталога для

файлы пакета maple2e находятся в каталоге ETC.

размещения

графических файлов

можно

отказаться

от

использования

В Maple не предусмотрена языковая поддержка LaTeX, значит, для

фреймов.

русификации текста необходимо подключить соответствующие библиотеки.

Русификация будет зависеть от используемой версииLaTeX. Так, в случае

пакета MikTeX и кодировки Windows необходимо после строки с командой

\documentclass вставить следующие команды:

\usepackage[cpl251]{inputenc} \usepackage[russian]{babel}

После этого документ может быть обработан трансляторомLaTeX.

В результате будет получен DVI-файл, который может быть распечатан или

выведен на экран. Отметим, что для правильной работы транслятора файлы

пакета

maple2e

должны

находиться

каталоге

транслируемым

документом или в каталоге LaTeX со стилевыми файлами.

После трансляции документLaTeX отличается от исходного

документа. В частности, рисунок в форматеEPS будет иметь больший

размер и иное представление, чем оригинал, что объясняется спецификой

работы драйвера Maple преобразования рисунков в формат EPS.

Другим распространенным инструментом подготовки публикаций

является

текстовый

редактор Microsoft Word. Начиная с версии Maple 6.0

рабочий документ автоматически преобразуется со всеми формулами и

графиками

в RTF-формат,

что

позволяет

работать

полученным

документом в наиболее популярных текстовых редакторах (Microsoft Word,

Page Maker и Quark X Press). При преобразовании документа в этот формат

все графики

формулы

внедряются RTFв -файл

виде

растровых

графических объектов, причем при этом может произойти потеря качества

рисунка.

Начиная с версии 5.1 в Maple появилась функция перекодировки

рабочих

документов

вHTML-формат

(Hyper

Text

Markup

Language

125

126

Список использованной литературы

исчисление. М.: Эдиториал, 2000.

1)Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. М.: Наука. 1989.

2)Говоров В.М., Дыбов П.Т., Мирошин Н.В., Смирнова С.Ф. Сборник

конкурсных задач по математике(с методическими указаниями и решениями): Учебн. пособие. – 2-е изд. – М.: Наука. Гл. ред. физ.- мат.

лит, 1986. - 384 с.

3)Говорухин В.Н., Цибулин В.Г. Введение в Maple V. Математический пакет для всех. М.: Мир, 1997.

4)Голоскоков Д.П. Уравнения математической физики. Решение задач в системе Maple. Учебник для вузов – СПб.: Питер, 2004. – 539с.

5)Дьяконов В. Maple 6. Учебный курс. – СПб: Питер. 2001. - 544с.

6)Дьяконов В. Maple 7: учебный курс. – СПб: Питер, 2002. - 672 с.

7)Зеркина А.В., Картак В.В., Картак В.М. Многомерная геометрия и линейная алгебра: Курс лекций. – Уфа: РИО БашГУ, 2004. -120с.

8)Ильин В.А., Позняк Э.Г. Аналитическая геометрия. М.: Наука. 1970.

9)Ильин В.А., Позняк Э.Г. Линейная алгебра. М.: Наука. 1970.

10)Манзон Б. Maple V Power Edition. - М: Информационно-издательский дом Филинъ, 1998. - 224с.

11)Минорский В.П. Сборник задач по высшей математике. Изд-е 8-е. -

М., Наука, 1964. - 360с.

12)Никольский С.М. Курс математического анализа(2 т.). М.: Наука. 1991.

13)Прохоров Г..В, Колбеев В..В, Желнов К.И., Леденев М.А., Математический пакет Maple V Release 4. – Калуга: Облиздат,1998. – 200с.

14)Савотченко С.Е., Кузьмичева Т.Г. Методы решения математических задач в Maple: Учебное пособие – Белгород: Изд. Белаудит, 2001. – 116 с.

15)Сдвижков О.А. Математика на компьютере: Maple 8. – М.:СОЛОН-

Пресс, 2003. – 176с.

16)Сканави М.И., Егерев В.К., Кордемский Б.А., Зайцев В.В. и др. Сборник задач по математике для поступающих во втузы: Учебн. пособие. Изд-е 5-е, перераб. и доп. – М.: ВШ, 1998. - 431 с.

17)Тарасевич Ю. Ю. Численные методы на Mathcad’е. – Астраханский гос. пед. ун-т: Астрахань, 2000, 70с.

18)Филиппов А.Ф. Сборник задач по дифференциальным уравнениям.

Изд-е 5-е, испр. - М., Наука, 1979. - 128с

19) Эльсгольц	Л.Э. Дифференциальные	уравнения и вариационное
	127	128

Оглавление

Введение					3
ГЛАВА 1					5
Основные правила работы в Maple. Элементарная математика					5
Константы, арифметические операции и функции					7
Синтаксис команд					11
Последовательности, списки					11
Алгебраические и тригонометрические преобразования					12
Решение	алгебраических	и	тригонометрических	уравнений	и
неравенств					15
Лабораторная работа № 1
Функции. Преобразование математических выражений					19
ГЛАВА 2					24
Геометрические построения на плоскости и в пространстве					24
Лабораторная работа № 2
Графика Maple . Решение алгебраических и тригонометрических
уравнений и неравенств					30
ГЛАВА 3					36
Элементы математического анализа					36
Непрерывность функции и точки разрыва					38
Экстремумы. Наибольшее и наименьшее значение функции					39
Исследование функции по общей схеме					40
Аналитическое и численное интегрирование					41
Интегралы, зависящие от параметра. Ограничения для параметров					43
Векторный анализ					45
Вычисление суммы ряда и произведений					48
Разложение функции в степенной ряд и ряд Тейлора					49
Лабораторная работа № 3
Исследование функции. Интегрирование					51
ГЛАВА 4					55
Линейная алгебра					55
Действия с матрицами					55
Спектральный анализ матрицы					59
Системы линейных уравнений и матричные уравнения.					62

Лабораторная работа № 4

129

Линейная алгебра							63
ГЛАВА 5							68
Обыкновенные дифференциальные уравнения							68
Общее решение обыкновенных дифференциальных уравнений							68
Фундаментальная (базисная) система решений							69
Решение задачи Коши или краевой задачи							70
Приближенное решение дифференциальных уравнений с помощью
степенных рядов							71
Численное	решение дифференциальных			уравнений		с помощью
команды	dsolve.	Построение		графиков			решений
дифференциальных уравнений с помощью команды odeplot							73
Структура DESol							76
Пакет Detools							78
Лабораторная работа №5
Решение	дифференциальных		уравнений		и	их	. систем
Геометрические построения, связанные с ОДУ							83
ГЛАВА 6							87
Дифференциальные уравнения с частными производными							87
Решение дифференциальных уравнений с частными производными							87
Пакет PDEtools							89
Пример решения смешанной задачи для уравнения теплопроводности
методом Фурье							92
Лабораторная работа		6№. Применение		метода		разделения
переменных							97
ГЛАВА 7							100
Процедуры
Определение и вызов процедур							100
Передача параметров							102
Локальные и глобальные переменные							105
Параметры описания процедур							106
Возвращаемые значения							107
ГЛАВА 8							113
Взаимодействие Maple с другими программами
Генерация кодов Maple в С и Фортран							113
Преобразование документов Maple в форматы LaTeX, RTF, HTML							116
			130

Список использованной литературы

120

131

132

<<< < Предыдущая 1 23 / 33

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.11.2019237.06 Кб28Pod_zvon_gitary_shestistrunnoy.doc
#
18.03.2016582.6 Кб690poliolimp_1-2.pdf
#
17.05.2015290.82 Кб35polozhenie_po_kursovim_1 (1).doc
#
17.05.2015289.79 Кб45polozhenie_po_kursovim_1_1.doc
#
21.09.201947.28 Кб37Polozhenie_po_praktike.docx
#
17.05.2015948.67 Кб70posobie_Maple.pdf
#
17.11.201916.77 Mб162Posobie_po_AYa_-_Sbornik_uprazhneny_1_kurs_nach...doc
#
09.11.20192.29 Mб38pourochnye_razrabotki_russkiy_yazyk_5_klass..doc
#
17.05.201542.85 Кб24PPD.docx
#
27.11.2019199.17 Кб21Prakticheskaya_rabota_5.doc
#
27.11.2019164.82 Кб9Prakticheskie_zanyatia_po_istorii (1).docx