ЛАБОРАТОРНАЯ РАБОТА № 1 ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ МЕТОДОМ

НАИМЕНЬШИХ КВАДРАТОВ

1.1Цель работы

Освоение обработки экспериментальных данных методом наименьших квадратов.

1.2Постановка задачи

Экспериментальные данные, полученные в лабораторных или промышленных условиях, являются основой для проведения дальнейших исследований.

Эти данные обычно используются:

-для определения констант известных теоретических соотношений (коэффициент диффузии, массопередачи и др.);

-как исходный материал для установления аналитических зависимостей (зависимость константы скорости реакции от температуры, зависимости плотности смеси от состава и т.д.).

Во втором случае в результате проведения эксперимента исследователь получает некоторую таблицу значений функции y при фиксированных значениях аргумента x:

Если аналитическое выражение наблюдаемой зависимости между y и x неизвестно, то встает практически важная задача - найти эмпирическую зависимость

расчеты по которой либо совпадают, либо приближаются наилучшим образом к экспериментально наблюдаемым значениям.

Геометрически задача построения эмпирической зависимости (1.1) состоит в том, чтобы построить некоторую кривую, которая была бы в определенном смысле близка к системе точек (xi, yi ), i=1,n.

Если вид зависимости заранее известен, то задача сводится к отысканию наилучших значений параметров этой зависимости, в противном случае вид этой зависимости также подлежит определению. По существу обе эти задачи решаются аналогично. Если вид зависимости y = f(x) заранее неизвестен, то исследователь по ряду соображений указывает узкий класс функций, которому должна принадлежать искомая функциональная зависимость. После того как выбран класс приближающих функций, не-

2

обходимо из него выбрать одну определенную функцию, воспользовавшись некоторым критерием оценки степени приближения.

1.3Аппроксимация экспериментальных данных методом наименьших квадратов

Пусть задана последовательность точек (xi, yi ),(i=1,n) и аппроксимируется зависимостью

Действительно, к виду (1.3) может быть приведен широкий класс функций. Например, зависимость f(x,a0 ,a1 ,a2 )=a0 +a1 x+a2 x2 может быть представлена в виде

данных является выбор метода отыскания наилучших значений параметров искомой зависимости. Наилучшие значения параметров ai (i=1,m) могут быть найдены относительно просто, для чего используется метод, называемый методом наименьших квадратов (МНК).

Согласно МНК наилучшими коэффициентами (в смысле приближения расчетных значений к экспериментальным) будут те, которые найдены исходя из условия минимума суммы квадратов отклонений экспериментальных значений от расчетных:

, ,…, , , ,…, , (1.5)

При фиксированных значениях xi функция Φ(a0 ,a1 ,...,am ) имеет минимум. Необходимым условием существования экстремума функции нескольких переменных является равенство нулю частных производных по каждой из переменных. Таким образом, аналитически существование экстремума выражения (1.5) запишется в виде

4

В некоторых случаях модели, нелинейные по параметрам, удается привести к линейному виду с помощью специальных преобразований. Например, уравнение

(1.9)

где а1, а2 - искомые параметры модели; х, у - входная и выходная координаты.

Введем обозначения lny = y1, lna1 = b0, a2 = b1, придем к линейному уравнению

у1 = b0 + b1x

Часто это не удается сделать. Например, уравнение

у

таким образом привести к линейному виду не представляется возможным. В этом случае процедура идентификации усложняется. Задача определения параметров нелинейной модели может быть сведена к минимиза-

ции суммы квадратов отклонений значений выходных координат yi и при одинаковых входных воздействиях х = хi:

(1.10)

Экстремум полученной функции также находится по соотношениям

Однако эти соотношения будут определять уже систему нелинейных алгебраических или трансцендентных уравнений, решение которых представляет самостоятельную и непростую задачу.

Параметры нелинейных моделей могут также находиться итеративно. Причем на каждой итерации исходная функция линеаризуется путем разложения в ряд Тейлора. Однако данный алгоритм может либо вообще не сходиться, либо сходиться очень медленно, с большими колебаниями оценок параметров.

В связи с этим более эффективным является непосредственный поиск экстремума функции Φ, основанный на использовании одного из методов оптимизации, например метода Ньютона.

1.4Порядок выполнения лабораторной работы

Постановка задачи: В таблице 1.1 приведены экспериментальные данные зависимости выходной координаты yэ от входной xэ. Целью лабораторной работы является подбор уравнения, которое описывало бы

5

наилучшим образом экспериментальные данные. Возможные варианты аппроксимирующих уравнений приведены в таблице 1.2. Ниже приведена и программа параметрической идентификации модели объекта.

Таблица 1.1 - Экспериментальные значения выходной координаты у

Таблица 1.2 − Аппроксимирующие формулы

1

2

1

3

6

Одним из универсальных способов решения рассматриваемой задачи с помощью программы EXCEL является использование поискового метода Ньютона.

Порядок выполнения работы следующий:

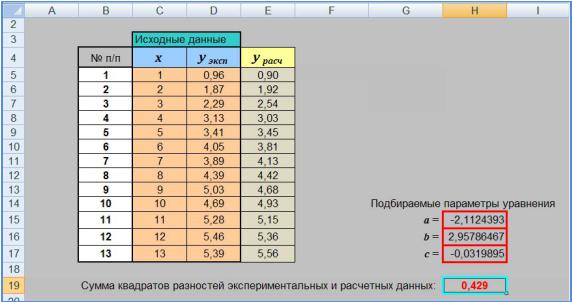
1)После запуска программы LP1.XLS вводятся исходные данные в

окне, приведенном на рисунке 1.3. В столбце обозначенной урасч вводят расчётные формулы из таблицы 1.2 и в ячейках, обозначенных буквами a, b, c, вводят примерные значения подбираемых параметров аппроксимирующего уравнения.

2)В ячейки, обозначенной «Сумма квадратов разностей», рассчитывается функция минимизации по формуле

и по её значению оценивается качество описания экспериментальных данных.

Таблица 1.3 – Окно ввода исходных данных

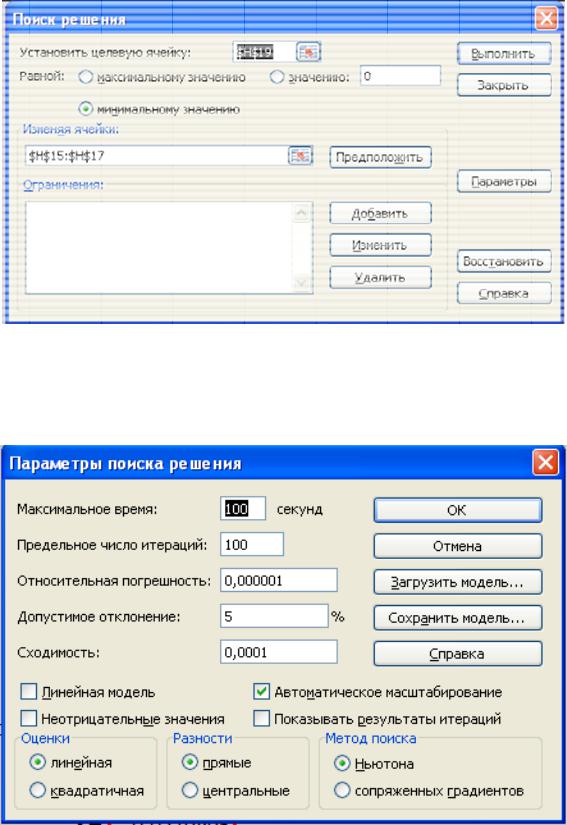
3) Для выполнения решения поставленной задачи надо войти в позицию Сервис/Поиск решения. На экране раскроется диалоговое окно Поиск решения (см. рисунок 1.4).

•Установите целевую ячейку. Для этого в текстовом поле необходимо указать адрес ячейки ($H$19), в которой вычисляются значения Φ по формуле (1.11).