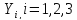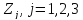-
Проверим продуктивность матрицы а;
Достаточным условием продуктивности является требование, чтобы суммы элементов столбцов матрицы были меньше 1. Непосредственной проверкой устанавливаем, что для заданной матрицы это требование выполняется.
Вычислим обратную матрицу:
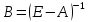
Вычисления производятся по формуле:
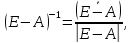
где:
 – определитель
матрицы;
– определитель
матрицы;
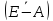 – присоединенная
матрица, которая образована алгебраическими
дополнениями элементов транспонированной
матрицы
– присоединенная
матрица, которая образована алгебраическими
дополнениями элементов транспонированной
матрицы
 .
.

Находим
определитель
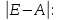
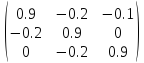 =0.9*0.9*0.9+(-0.2)*0*0+(-0.1)*(-0.2)*(-0.2)-(-0.1)*0.9*0-0.9*0*(-0.2)-(-0.2)*(-0.2)*0.9=0.729-0.004-0.036=0.689
=0.9*0.9*0.9+(-0.2)*0*0+(-0.1)*(-0.2)*(-0.2)-(-0.1)*0.9*0-0.9*0*(-0.2)-(-0.2)*(-0.2)*0.9=0.729-0.004-0.036=0.689
Транспонируем матрицу B, то есть:
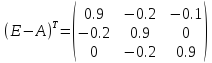 =
=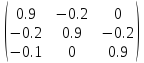
Находим алгебраические дополнения:
В матрице вычеркиваем строку 1 и столбец 1.
|
M1,1 = |
|
== |
00.81 |
|||||
|
A1,1 = (-1)1+1M1,1 = |
0.81 |
|||||||
В матрице вычеркиваем строку 1 и столбец 2.
|
M1,2 = |
|
= |
-0.2 |
|||||
|
A1,2 = (-1)1+2M1,2 = |
0.2 |
|||||||
В матрице вычеркиваем строку 1 и столбец 3.
|
M1,3 = |
|
= |
0,09 |
|||||
|
A1,3 = (-1)1+3M1,3 = |
0.09 |
|||||||
В матрице вычеркиваем строку 2 и столбец 1.
|
M2,1 = |
|
= |
-0.18 |
|||||
|
A2,1 = (-1)2+1M2,1 = |
0.18 |
|||||||
В матрице вычеркиваем строку 2 и столбец 2.
|
|
|
M2,2 = |
|
= |
00.81 |
||||||||
|
|
|
|
|
||||||||||
|
A2,2 = (-1)2+2M2,2 = |
0.81 |
||||||||||||
В матрице вычеркиваем строку 2 и столбец 3
|
M2,3 = |
|
= |
-0.02 |
|||||
|
A2,3 = (-1)2+3M2,3 = |
0.02 |
|||||||
В матрице вычеркиваем строку 3 и столбец 1.
|
M3,1 = |
|
= |
00.04 |
|||||
|
A3,1 = (-1)3+1M3,1 = |
0.04 |
|||||||
В матрице вычеркиваем строку 3 и столбец 2.
|
M3,2 = |
|
= |
-0.18 |
|||||
|
A3,2 = (-1)3+2M3,2 = |
0.18 |
|||||||
В матрице вычеркиваем строку 3 и столбец 3.
|
M3,3 = |
|
= |
00.77 |
|||||
|
A3,3 = (-1)3+3M3,3 = |
0.77 |
|||||||
Выпишем матрицу алгебраических дополнений:
|
|
|

Проверим результаты вычислений с помощью программного продукта MSExcel (функции МОБР):
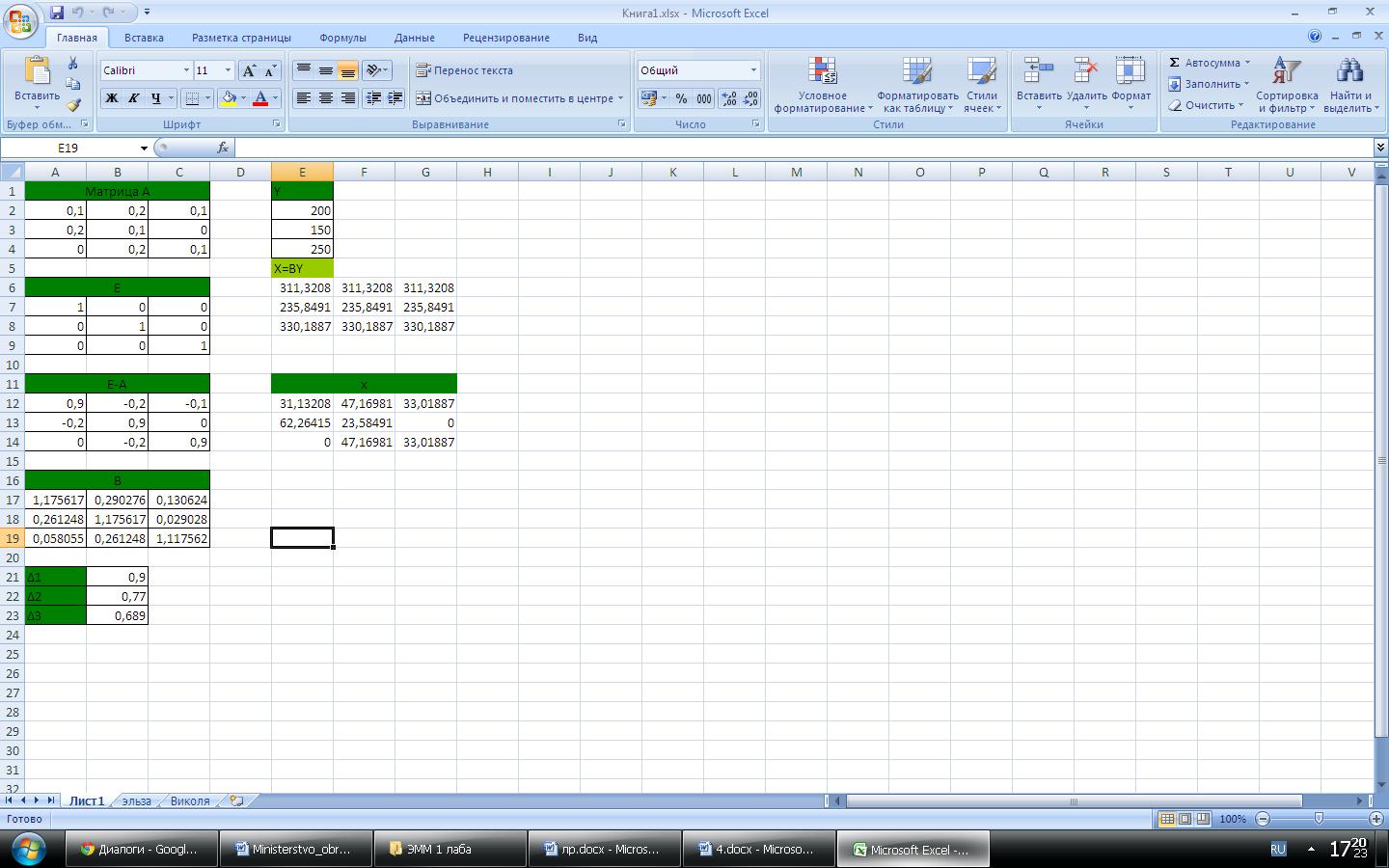
Рис. 1 – Результаты вычислений обратной матрицы
Все элементы матрицы B не отрицательны, это подтверждает что матрица Aпродуктивна.
Находим вектор валовой продукции:

Проверим найденное решение, с помощью MSExcel:
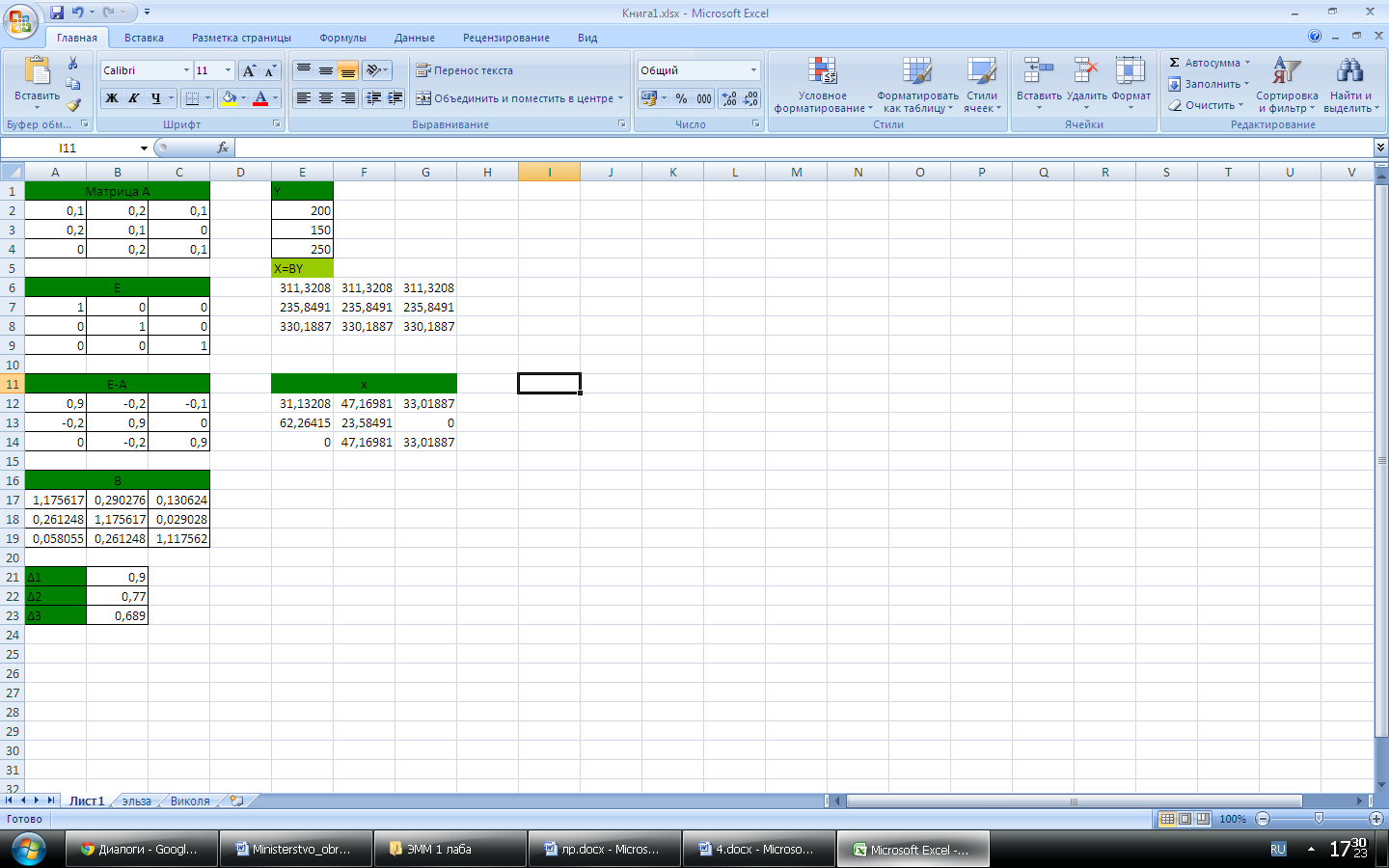
Рис. 2 – Результаты вычислений вектора валовой продукции
Найдём
межотраслевые поставки
 ,
которые вычисляются по формуле:
,
которые вычисляются по формуле:
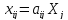 .
.
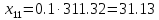
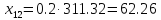
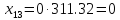
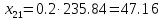
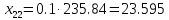
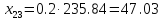
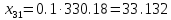
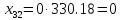
Проверим найденное решение, с помощью MS Excel:
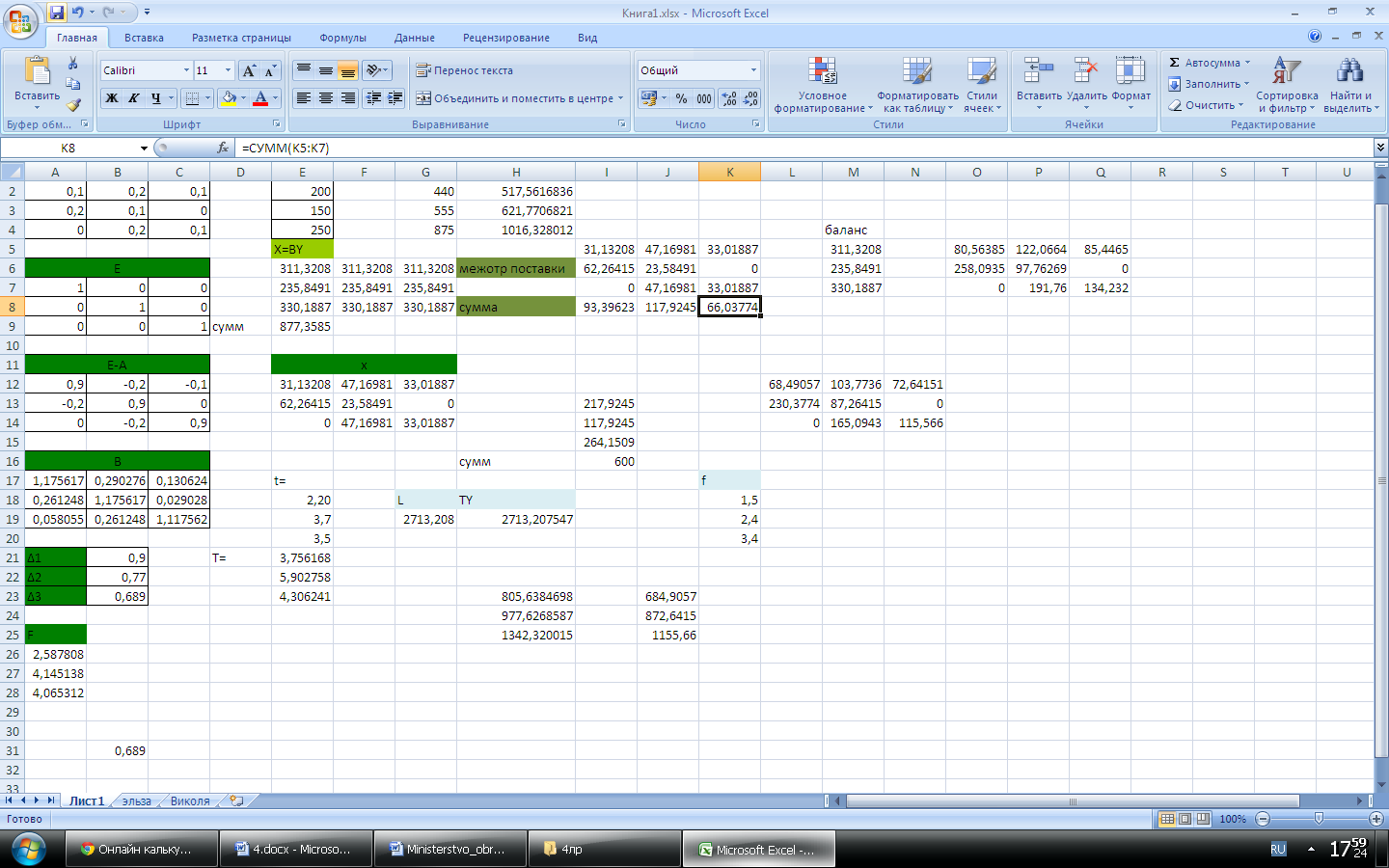
Рис. 3 – Результаты вычислений межотраслевых поставок.
Заполним схему Межотраслевого баланса:
Таблица 4 - МОБ
|
Производящие отрасли |
Потребляющие отрасли |
Конечная
продукция
|
Валовая
продукция
|
||||
|
1 |
2 |
3 |
|
|
|||
|
1 |
31,13208 |
47.16 |
33.01 |
200 |
311.32 |
||
|
2 |
62,269 |
23,58 |
0 |
150 |
235.45 |
||
|
3 |
0 |
47,16 |
33,01 |
250 |
330.18 |
||
|
Материальные издержки |
93.39 |
117.92 |
66.03 |
|
|
||
|
Условно-чистая
продукция
|
217,93 |
117,53
|
264,15
|
600 |
|
||
|
Валовая продукция |
311.32 |
235.45 |
330.18 |
|
877,35 |
||
Из таблицы 4, видно что:
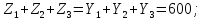
Соблюдается принцип единства стоимостного и материального состава национального дохода.

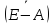 =
=