Исходные данные к задаче № 6

Вариант	Величины
	, В	, Ом	Фаза А		Фаза B		Фаза С
				характер нагрузки		характер нагрузки		характер нагрузки
1	220	5	1	R	0,866	R,	0,866	R,
2	380	10	0		1	R	0
3	660	12,7	1	R	0		0
4	220	20	0		1	R	0
5	380	25	1	R	0		0
6	660	30	0		0		1	R
7	220	35	0,5	R,	0,5	R,	0,5	R,
8	380	40	0,866	R,	0,866	R,	1	R
9	660	44	1	R	0		0
10	220	50	1	R	0		0
11	380	55	0		1	R	0
12	660	60	0,5	R,	1	R	1	R
13	220	80	1	R	0		0
14	380	100	0		1	R	0
15	660	127	0,705	R,	0,705	R,	1	R
16	220	5	1	R	0		0
17	380	10	1	R	0		0
18	660	10	1	R	0,5	R,	0,5	R,
19	220	12,7	0		1	R	1	R
20	380	12,7	0,705	R,	0,705	R,	0,705	R,
21	660	20	0		0		1	R
22	220	22	1	R	1	R	0,5	R,
23	380	24	0,866	R,	1	R	0,866	R,
24	660	25	0		0		1	R
25	220	30	0		0		1	R

Ход решения задачи

Трехфазная система питания электрических цепей представляет собой совокупность трех синусоидальных эдс или напряжений, одинаковых по частоте и амплитудному значению, сдвинутых по фазе относительно друг друга на угол , т. е. на 120.

При соединении фаз трехфазного источника питания или потребителя электроэнергии по схеме «звезда» напряжения ,,, действующие между началами и концами фаз потребителя, называются фазными напряжениями. Напряжения,,, действующие между началами фаз потребителя, являются линейными напряжениями.

Линейные токи в питающих линиях (,,) при соединении трехфазного источника питания и трехфазного потребителя электроэнергии по схеме «звезда» одновременно являются и фазными токами, протекающими по фазам потребителя (,,).

Линейные напряжения при соединении трехфазного источника питания и трехфазного потребителя электроэнергии по схеме «звезда» отличаются от фазных в раз:

.

 Расчет токов проводят с применением символического метода на основе закона Ома, предварительно выразив фазные напряжения и сопротивления каждой фазы приемника в виде комплексного числа, в котором действительной частью является активное сопротивление, а мнимой частью – реактивное сопротивление:

; ;;

 

; ;;

 

; ;,

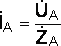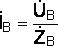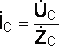где – фазные напряжения потребителей, В;,– модуль и фаза сопротивления нагрузки.

Комплексный ток в нейтральном проводе находят в соответствие с уравнением, составленным по первому закону Кирхгофа для нейтральной точки n:

.

 Комплексный ток в нейтральном проводе можно найти из векторной диаграммы, сложив векторы фазных токов, как показано на рис. 6.1.

 

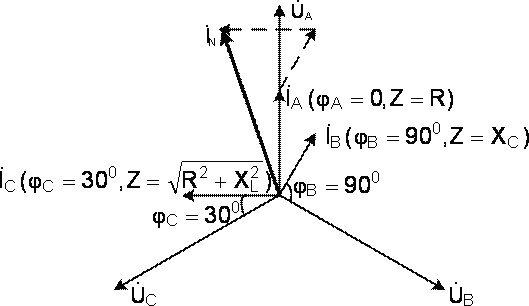
 Рис. 6.1. Векторная диаграмма токов и напряжений

Трехфазная четырехпроводная система обеспечивает потребителя электроэнергии симметричным питанием. При этом активная, реактивная и полная мощности могут быть определены по следующим формулам с учетом знака реактивных сопротивлений:

;

;

,

где P, Q, S – активная, реактивная и полная мощности соответственно;  R, X – активное и реактивное сопротивления каждой фазы.

 

Задача № 7

РАСЧЕТ ТРЕХФАЗНЫХ ЧЕТЫРЕХПРОВОДНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

В трехфазную четырехпроводную электрическую сеть с симметричными фазными эдс включены три потребителя электроэнергии с сопротивлениями ,и, соединенные по схеме «звезда». Составить электрическую схему питания потребителей электроэнергии с указанием токов и напряжений, действующих в системе, и с учетом приведенных в табл. 7.1 для каждого варианта задания данных, определить фазные напряжения,и, напряжение смещения, падение напряженияна сопротивлениинейтрального провода, фазные токи,и, токв нейтральном проводе, фазные коэффициенты мощности,,, активные,,, реактивные,,и полные,,мощности фаз, а также активную, реактивнуюи полнуюмощности трехфазного потребителя электроэнергии. Внутренними сопротивлениями источников эдс пренебречь.

Построить векторную диаграмму напряжений и токов на плоскости комплексных чисел.

Таблица 7.1