2. Принцип Ферма. Оптическая длина пути. Таутохронность и стационарность пути. Примеры.

Принцип Ферма гласит: из всех возможных путей между двумя точками свет проходит по тому, по которому время прохождения наименьшее.

Из принципа Ферма следует, что в однородной среде (в такой среде скорость света всюду одинакова) свет должен распространяться прямолинейно: прямая - кратчайшее расстояние между двумя точками, следовательно, и время распространения - наименьшее.

Покажем теперь, что закон отражения света - тоже прямое следствие принципа Ферма.

Из принципа Ферма можно получить и закон преломления света (точнее - световых лучей). Здесь речь идет о переходе света из одной среды в другую через границу раздела между ними. Различие сред состоит в том, что в них различны скорости распространения света.

В этом и заключается закон преломления для нашего случая: отношение синуса угла падения к синусу угла преломления равно отношению скоростей распространения света в вакууме и в среде, которая с ним граничит. Отношение - величина постоянная, характерная для данной среды. Она называется показателем преломления вещества и обозначается буквой n, так что sinα/sinβ = n. В общем случае, когда свет переходит из произвольной среды, в которой скорость света равна υ1, в среду со скоростью света в ней υ2, закон преломления имеет вид sinα/sinβ = n₂₁, где n₂₁ - относительный показатель преломления сред 2 и 1.

Оптической длиной пути называется произведение геометрической длины d пути световой волны в данной среде на абсолютный показатель преломления этой среды n.

Если оптические длины пути двух лучей равны, то такие пути называются таутохронными (не вносящими разности фаз). В оптических системах, дающих стигматические изображения источника света, условию таутохронности удовлетворяют все пути лучей, выходящих из одной и той же точки источника и собирающихся в соответствующей ей точке изображения.

Например, при попадании светового луча внутрь стеклянного параллелепипеда принцип Ферма подскажет нам, на какой угол преломится луч. Весь вопрос сведется к тому, по какому пути должен распространяться луч внутри стекла, чтобы на это ушел минимум времени, учитывая, что в стекле свет распространяется медленнее, чем в воздухе. Поскольку луч в стекле затормаживается, он неизбежно отклонится от направления, под которым он вошел в стекло, иначе возрастет время луча в пути. С другой стороны, если луч внутри стекла пойдет строго перпендикулярно к поверхности стекла, это приведет к увеличению общего пути, пройденного лучом, включая отрезки за пределами стекла, и, как следствие, также к увеличению затраченного времени. Следовательно, для нахождения кратчайшей по времени траектории пути луча между двумя точками нужно найти компромисс между увеличением совокупного пути луча и сокращением пути луча в тормозящей его среде.

3. Применение принципа Ферма для получения основных законов геометрической оптики.

Как ответ на 2 вопрос

4. Тонкая линза. Формула тонкой линзы. Фокусное расстояние. Формула тонкой линзы.

Линза может быть ограничена двумя выпуклыми сферическими поверхностями (двояковыпуклая линза - рис. а), выпуклой сферической поверхностью и плоскостью (плоско-выпуклая линза - рис. б), выпуклой и вогнутой сферическими поверхностями (вогнуто-выпуклая линза - рис. в). Эти линзы посередине толще, чем у краев, и все они называются выпуклыми:

Линзы, которые посередине тоньше, чем у краев, называются вогнутыми. На рисунке изображены три вида вогнутых линз: двояковогнутая -а, плосковогнутая -б, выпукло-вогнутая -в:

Тонкая линза.

Мы будем рассматривать наиболее простой случай, когда толщина линзы l=|AB| пренебрежимо мала по сравнению с радиусами R1 и R2 поверхностей линзы и расстоянием предмета от линзы.

Такую линзу называют тонкой линзой. В дальнейшем, говоря о линзе, будет подразумеваться именно тонкая линза.

Точки А и B в тонкой линзе расположены столь близко друг к другу, что их можно принять за одну точку, которую называют оптическим центром линзы и обозначают точкой О. Луч света, проходящий через оптический центр линзы, практически не преломляется.

П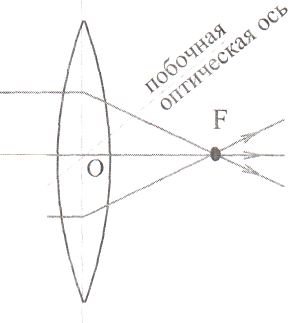рямую Q₁Q₂, проходящую через центры сферических поверхностей, которые ограничивают линзу, называют ее главной оптической осью. Главная оптическая ось тонкой линзы проходит через оптический центр. Любую другую прямую, проходящую через оптический центр, называют побочной оптической осью. Подобно плоскому зеркалу линза создает изображения источников света. Это означает, что свет, исходящий из какой-либо точки предмета (источника), после преломления в линзе снова собирается в одну точку (изображение), независимо от того, через какую часть линзы прошли лучи. Если по выходе из линзы лучи сходятся, они образуют действительное изображение. В случае же, когда прошедшие через линзу лучи являются расходящимися, пересекаются в одной точке не сами лучи, а их продолжения. Изображение тогда мнимое. Его можно наблюдать глазом непосредственно или с помощью оптических приборов. Точка, в которой пересекаются после преломлений в собирающей линзе лучи, падающие на линзу параллельно главной оптической оси, называется главным фокусом линзы. Эту точку обозначают буквой F.

главная оптическая ось

Пустим три параллельных луча под углом к главной оптической оси. Мы увидим тогда, что пересечение произойдет не в главном фокусе линзы, а в другой точке. Точки пересечения лучей, падающих на линзу параллельными пучками, и при различных углах, образуемых этими пучками с главной оптической осью, располагаются в плоскости, перпендикулярной главной оптической оси и проходящей через главный фокус.

Фокальная плоскость

Вогнутые линзы являются рассеивающими. Преломленные лучи будут расходящимися, а их продолжения пересекаются в главном фокусе рассеивающей линзы. В этом случае главный фокус является мнимым, и находится на расстоянии F от линзы.

Формула тонкой линзы

Величина d - расстояние от предмета до линзы, величина F- расстояние от линзы до изображения, Формула тонкой линзы:

1/F = 1/f + 1/d

Величины d, f, F могут быть как положительными, так и отрицательными. Если линза собирающая, то ее фокус действительный, и перед членом «1//F/» ставится знак «+». В случае рассеивающей линзы F больше 0 и в правой части формулы будет стоять отрицательная величина - «1//F/». Перед членом «1//f/» ставится знак «+», если изображение действительное, и знак «-», если изображение мнимое. Перед членом «1//d/» ставят знак «+» в случае действительной светящейся точки, и «-», если она мнимая (т.е. на линзу падает сходящийся пучок лучей, продолжения которых пересекаются в одной точке).