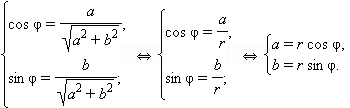1. Комплексные числа Обозначим через С множество пар упорядоченных действительных чисел: . Определение. Упорядоченную пару действительных чисел  называют комплексным числом. Пусть , .

Операция сложения. Определение. Сложением двух комплексных чисел  и  называется такое комплексное число  с координатами , где , , т.е. . Свойства:

• ;

• 

• ;

• для 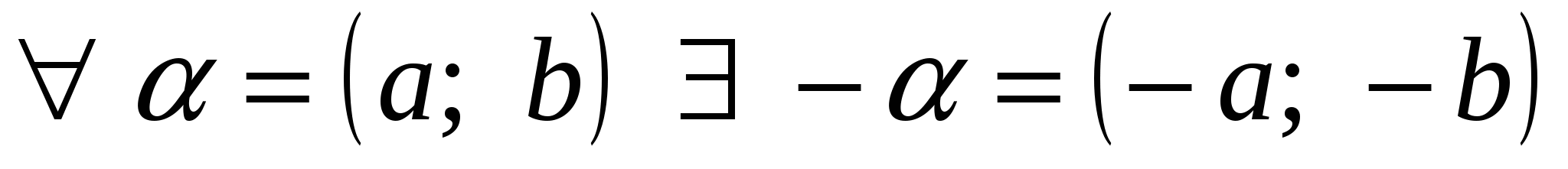, что .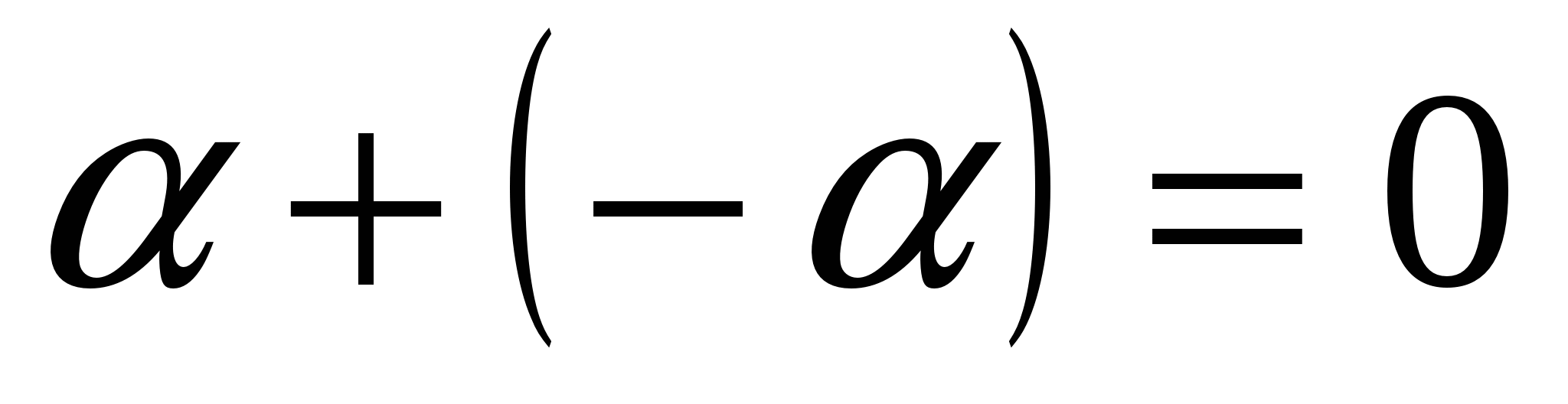

Операция умножения. Определение. Произведением двух комплексных чисел  и  называется такое комплексное число  с координатами , где , , т.е. . Свойства:

• ;

• 

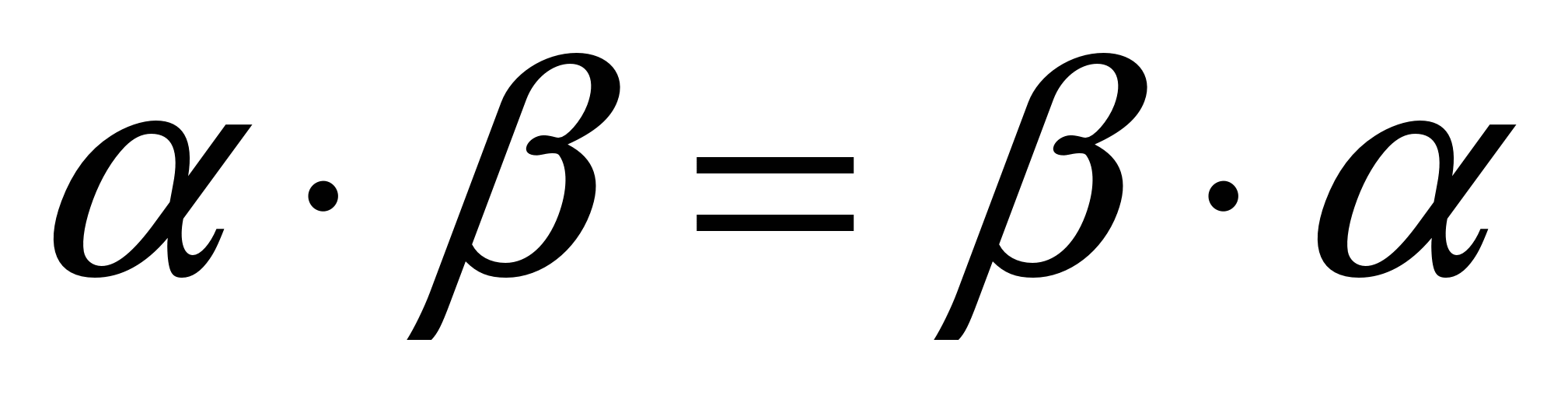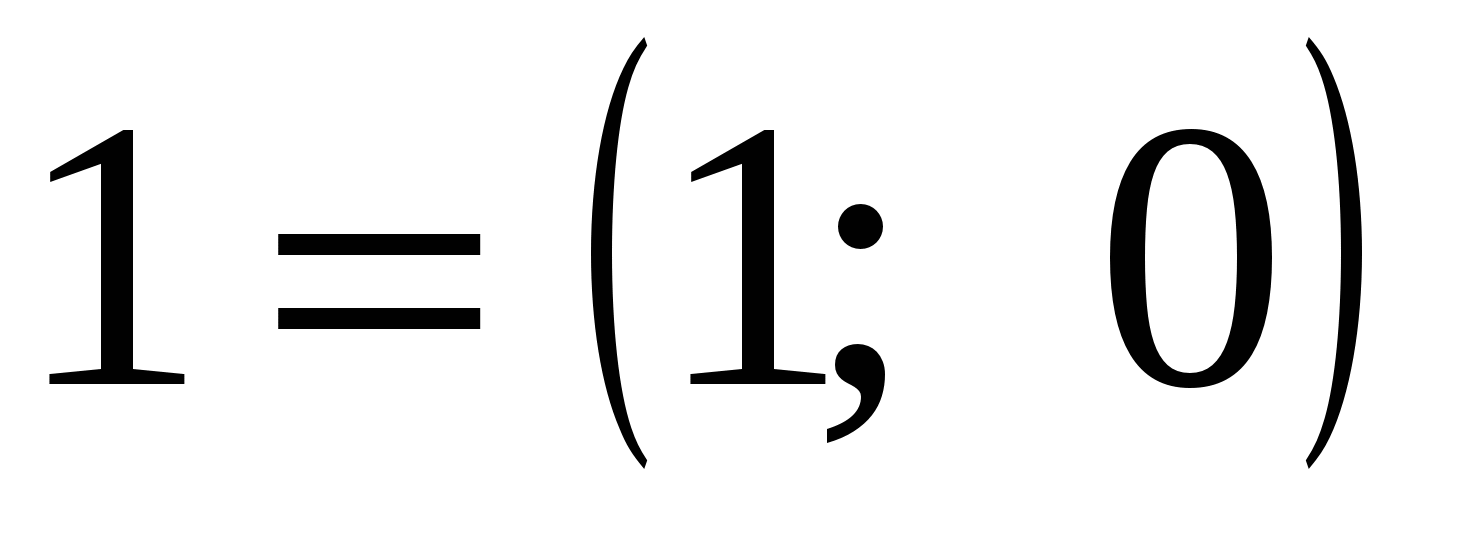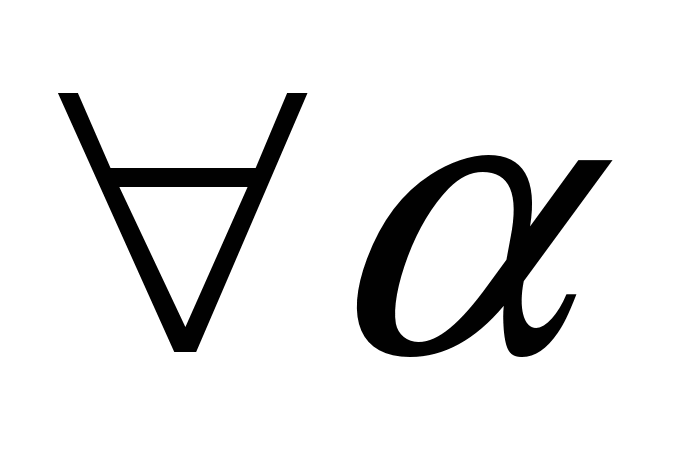
• , для  , что ;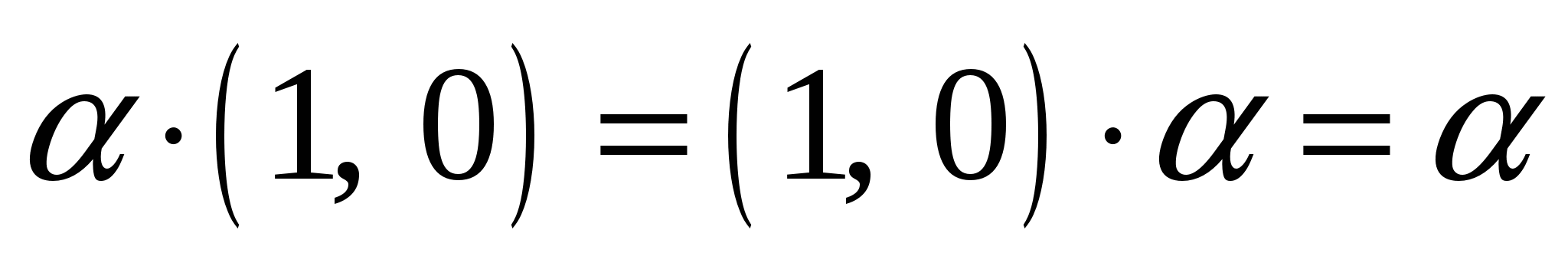

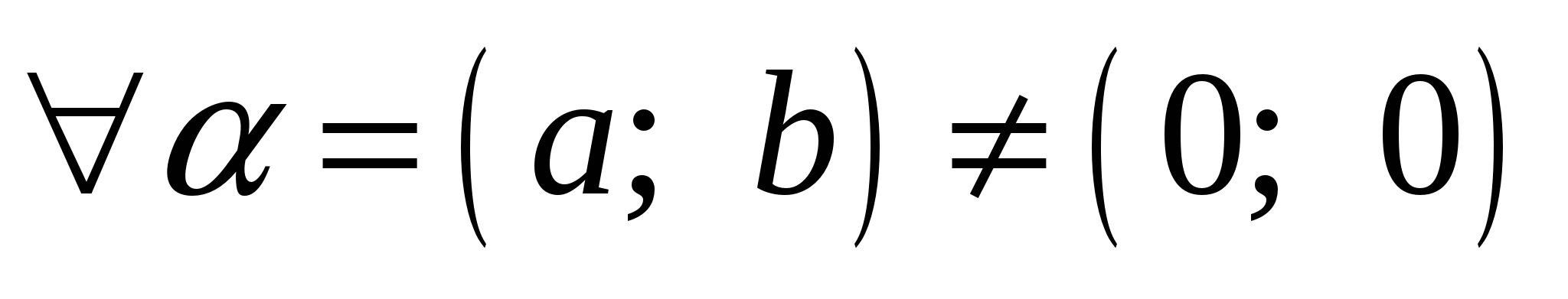
• для  , что .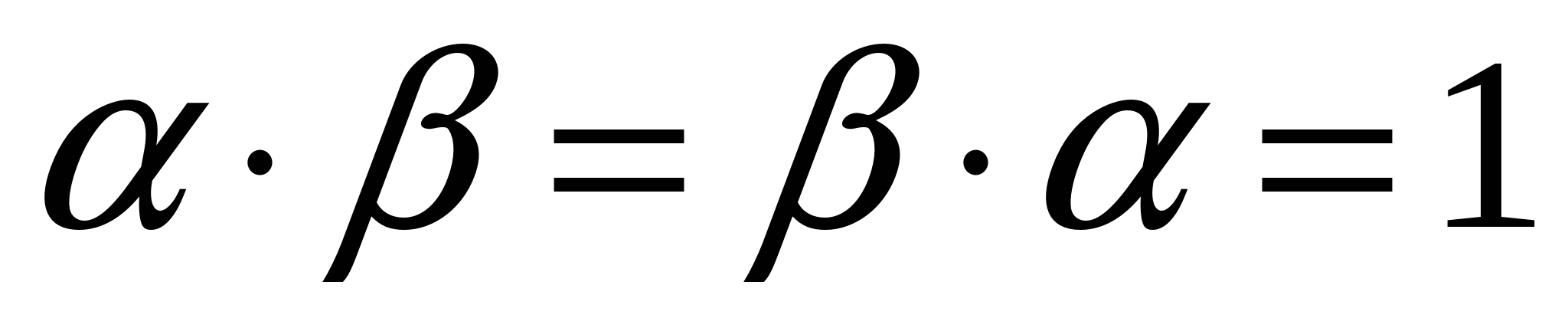

Если комплексное число имеет вид , то данное число находится на числовой оси  и можно записать просто в виде действительного числа , следовательно . Если обозначить , то получим, что  Таким образом любое комплексное число  можно записать в другом виде:  , здесь  и – действительные числа,  мнимое число.

2) Комплексным числом z называется пара (x, y) действительных чисел x и y. При этом равенство, сумма и произведение упорядоченных пар, а также отождествление некоторых из них с действительными числами определяются следующим образом:

1) два комплексных числа z₁ = (x₁, y₁) и z₂ = (x₂, y₂) называются равными, если x₁ = x₂ и y₁ = y₂;

2) суммой комплексных чисел z₁ и z₂ называется комплексное число z вида

z = (x₁ + x₂, y₁ + y₂);

3) произведением комплексных чисел z₁ и z₂ называется комплексное число

z = (x₁x₂ - y₁y₂, x₁y₂ + x₂y₁);

4) множество комплексных чисел , отождествляется с множеством действительных чиселR.

Разностью комплексных чисел z₁ и z₂ называется комплексное число z такое, что z₂ + z = z₁, откуда находим z = z₁ - z₂ = (x₁ - x₂, y₁ - y₂).

Частным комплексных чисел z₁ и z₂ называется комплексное число z такое, что . Отсюда находим

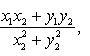
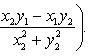
Комплексное число (0, 1) обозначается символом i = (0, 1). Тогда , т. е. i² = -1. Произвольное комплексное число z можно записать в виде

z = (x, y) = (x, 0) + (0, y) = (x, 0) + (0, 1)(y, 0) = x + iy.

Эта запись называется алгебраической формой комплексного числа. Комплексное число  называется сопряженным по отношению к комплексному числу z = (x, y) = x + iy.

Модулем комплексного числа называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длинарадиус-вектора, который на чертеже обозначен красным цветом.

Модуль комплексного числа стандартно обозначают: или 

По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: . Данная формула справедлива для любых значений «а» и «бэ».

Аргументом комплексного числа называется угол между положительной полуосьюдействительной оси и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: .

Аргумент комплексного числа стандартно обозначают: или 

3) Та запись комплексного числа, которую мы использовали до сих пор, называется алгебраической формой записи комплексного числа. Часто бывает удобна немного другая форма записи комплексного числа. Пусть  и φ = arg z. Тогда по определению аргумента имеем: 

Отсюда получается 

z = a + bi = r(cos φ + i sin φ).

Такая форма называется тригонометрической формой записи комплексного числа. Как видно, для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.

.2. Деление комплексных чисел в тригонометрической форме записи.

Теорема. (О делении комплексных чисел в тригонометрической форме)

Пусть , где и , где – два произвольных комплексных числа записанных в тригонометрической форме. Тогда

             .                (2)

   Доказательство. Воспользуемся следствием формулы Муавра и правилом умножения комплексных чисел в тригонометрической форме записи. Получаем:

 

, ч.т.д.

Пример 1. Запишите комплексные числа и в тригонометрической форме и найдите их произведение и частное .

Решение. 1) Комплексное число на комплексной плоскостинаходится во второй четверти, поэтому

, .

2) Комплексное число на комплексной плоскости находится во четвертой четверти, поэтому

, .

3) 

.

Ответ: , 

Возведение комплексных чисел в степень

Начнем со всем любимого квадрата.

Пример 9

Возвести в квадрат комплексное число 

Здесь можно пойти двумя путями, первый способ это переписать степень как произведение множителей и перемножить числа по правилу умножения многочленов.

Второй способ состоит в применение известной школьной формулы сокращенного умножения :

Для комплексного числа легко вывести свою формулу сокращенного умножения: . Аналогичную формулу можно вывести для квадрата разности, а также для куба сумма и куба разности. Но эти формулы более актуальны длязадач комплексного анализа, поэтому на данном уроке я воздержусь от подробных выкладок.

Что делать, если комплексное число нужно возвести, скажем, в 5-ую, 10-ую или 100-ую степень? Ясно, что в алгебраической форме проделать такой трюк практически невозможно, действительно, подумайте, как вы будете решать пример вроде ?

И здесь на помощь приходит тригонометрическая форма комплексного числа и, так называемая, формула Муавра: Если комплексное число представлено в тригонометрической форме , то при его возведении в натуральную степень справедлива формула:

Пример 12

Возвести в степень комплексные числа , , 

Здесь тоже всё просто, главное, помнить знаменитое равенство.

Если мнимая единица возводится в четную степень, то техника решения такова:

Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и»,  получая четную степень:

Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить:

4) Виды матриц

1. Прямоугольные: m и n - произвольные положительные целые числа

2. Квадратные: m=n

3. Матрица строка: m=1. Например, (1 3 5 7 ) - во многих практических задачах такая матрица называется вектором

4. Матрица столбец: n=1. Например

5. Диагональная матрица: m=n и a_ij=0, если i≠j. Например

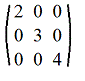
6. Единичная матрица: m=n и

7. Нулевая матрица: a_ij=0, i=1,2,...,m

j=1,2,...,n

8. Треугольная матрица: все элементы ниже главной диагонали равны 0.

Пример.

9. Симметрическая матрица: m=n и a_ij=a_ji (т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательно A'=A

Например,

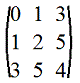
10. Кососимметрическая матрица: m=n и a_ij=-a_ji (т.е. на симметричных относительно главной диагонали местах стоят противоположные элементы). Следовательно, на главной диагонали стоят нули (т.к. при i=j имеем a_ii=-a_ii)

Пример.

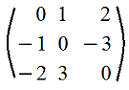
Ясно, A'=-A

11. Эрмитова матрица: m=n и a_ii=-ã_ii (ã_ji - комплексно - сопряженное к a_ji, т.е. если A=3+2i, то комплексно - сопряженное Ã=3-2i)

Пример

Действия над матрицами.

1. Сложение матриц - поэлементная операция

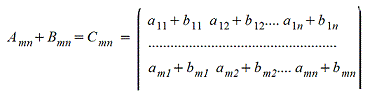
2. Вычитание матриц - поэлементная операция

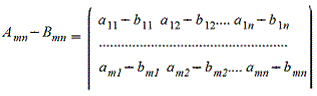
3. Произведение матрицы на число - поэлементная операция

4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)

A_mk*B_kn=C_mn причем каждый элемент с_ij матрицы C_mn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.

5. Возведение в степень

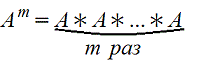
m>1 целое положительное число. А - квадратная матрица (m=n) т.е. актуально только для квадратных матриц

6. Транспонирование матрицы А. Транспонированную матрицу обозначают A^T или A'

5) Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Это многочлен, комбинирующий элементы квадратной матрицы таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов. Т.е., определитель характеризует содержание матрицы. В частности, если в матрице есть линейно-зависимые строки или столбцы определитель равен нулю. Определитель играет ключевую роль в решении в общем виде систем линейных уравнений, на его основе вводятся базовые понятия. В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.

Определитель матрицы А обозначается как: det(A), |А| или Δ(A).