3О. Условие совместности слу.

Теорема 2. (теорема Кронекерра–Капелли). Для того, чтобы система (1) была совместной, необходимо и достаточно, чтобы ранг ее расширенной матрицы был равен рангу основной матрицы, т.е.

.

Доказательство. Очевидно, что .

Для доказательства перепишем систему (1) в виде:

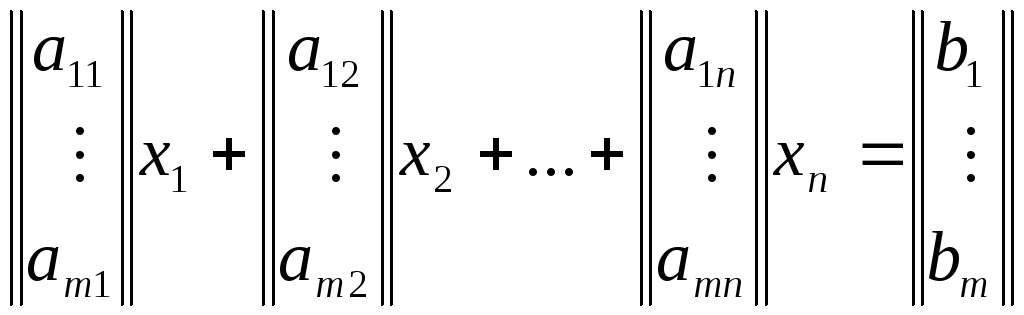(4)

где выделены столбцы матрицы , являющиеся элементами .

Необходимость. Если существует решение , то запись (4) означает, что столбец свободных членов есть линейная комбинация столбцов матрицы . Значит, добавление этого столбца не изменяет числа линейно независимых столбцов .

Достаточность. Пусть . В этом случае базисный минор матрицы является базисным и для . Это и означает, что столбец свободных членов есть линейная комбинация тех столбцов матрицы , в которых расположен базисный минор, а значит, и всех столбцов матрицы (остальные можно взять с коэффициентом 0). Очевидно, что коэффициенты этой линейной комбинации и являются решениями системы (1), т.е. есть хотя бы одно решение.

4О. Построение решений слу.

Теорема Кронекера–Капелли устанавливает совместимость СЛУ, но не дает практического рецепта их нахождения. Ниже дается один из возможных способов.

Пусть рассматривается произвольная система уравнений с неизвестными и пусть .

Определение 7. Число , равное рангу матриц и , называется рангом системы (1).

Не ограничивая общности, будем считать, что базисный минор матрицы расположен в левом верхнем углу (этого всегда можно добиться применением нумерации неизвестных и перестановкой уравнений). Обозначим этот минор :

.

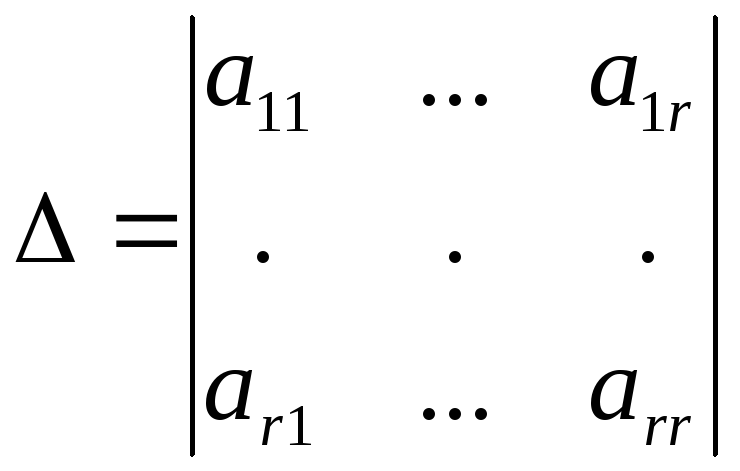Минор является базисным и для , поэтому строки матрицы с номерами , …, являются линейными комбинациями первых ее строк (теорема о базисном миноре). Это означает, что уравнения с номерами , …, представляют собой линейные комбинации первых уравнений, так что система (1) эквивалентна системе

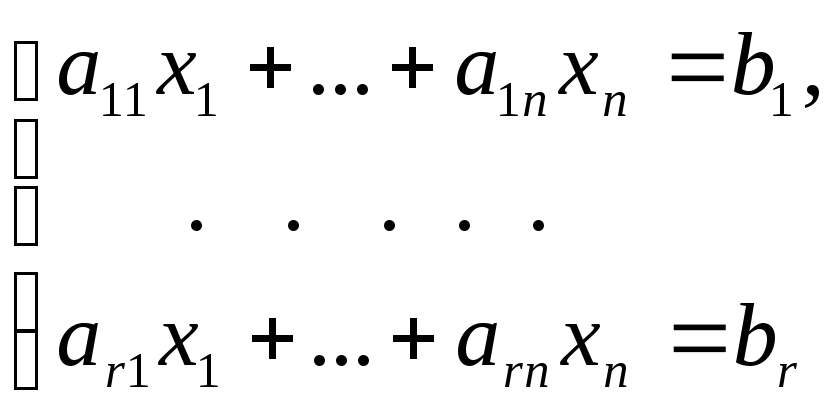(5)

(так как все решения (5) обращаются в тождество все последующие уравнения).

Если , то (5) система с определителем неравным нулю и она (и значит система (1)) имеет единственное решение, определяемое по правилу Крамера. Т.о., справедлива следующая теорема.

Теорема 3. Если , то система (1) имеет единственное решение.

Пусть далее . Оставим в левых частях лишь те слагаемые, коэффициенты которых образуют базисный минор , остальные перенесем вправо.

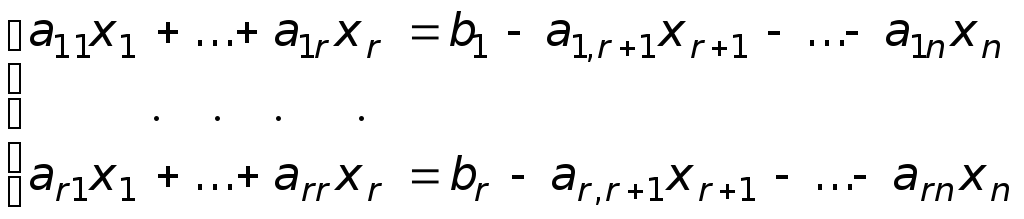(6)

Определение 8. Неизвестные называются базисными, а переменные – свободными.

Свободным переменным можно придать произвольные значения. Тогда базисные неизвестные определяются по формулам Крамера:

,

Здесь – определитель, получающийся из заменой -ого столбца на столбец свободных членов системы (6). Пользуясь свойствами определителя, последнюю формулу можно переписать в виде:

.

Введем обозначения: , .

Тогда имеем

.

Добавляя сюда очевидные равенства: , …, , имеем

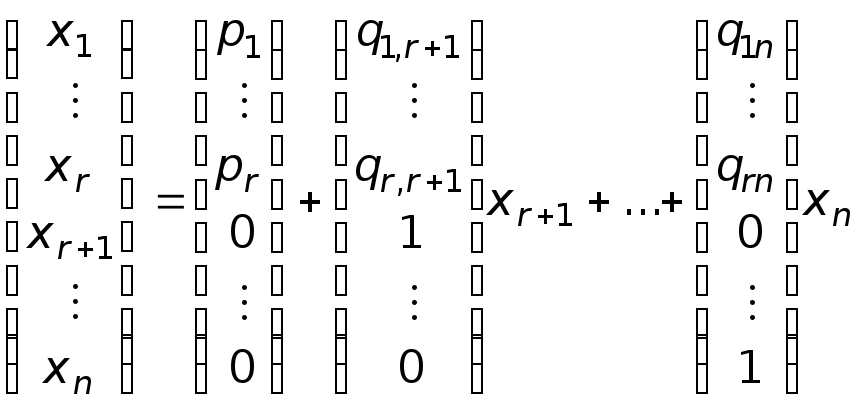(7)

Формулы (7) дают общее решение системы (1), т. к. выражают все неизвестные через свободные неизвестные .

Покажем, что формулы (7) содержат все варианты решения системы (1). В самом деле, если , – решение СЛУ (1), то имеют определенные числовые значения  подставляя их в систему (1) и повторяя все предыдущие выкладки, получим (7).

Таким образом, доказано.

Теорема 4. Если (1) совместна и ее ранг меньше , то эта система имеет бесконечное множество решений.