Приклади розв’язування задач

Приклад 1. Частинка здійснює гармонічні коливання вздовж осі х біля положення рівноваги х = 0. Циклічна частота коливань  = 4 c^-1. В момент часу t = 0 координати частинки х₀ = 25,0 см, а її швидкість υ = 100 см/с. Знайти координату х і швидкість υ цієї частинки через t = 2,40 с.

Дано:

 = 4 с^-1

х₀ = 25,0 см

υ= 100,0 см/с

t = 2,40 с

___________

х – ? υ – ?

Розв’язування. Рівняння гармонічних коливань має вигляд:

x = A cos ( t + ). (1)

Швидкість частинки в довільний момент часу дорівнює:

υ = - A  sin ( t + ) . (2)

В початковий момент часу t = 0 величини х і υ відповідно дорівнюють х₀ і υ₀:

x₀ = A cos  i υ₀ = - A sin  . (3)

Розв’язавши систему рівнянь (3), одержимо значення амплітуди коливань і початкової фази:

= 1 звідки А = ;

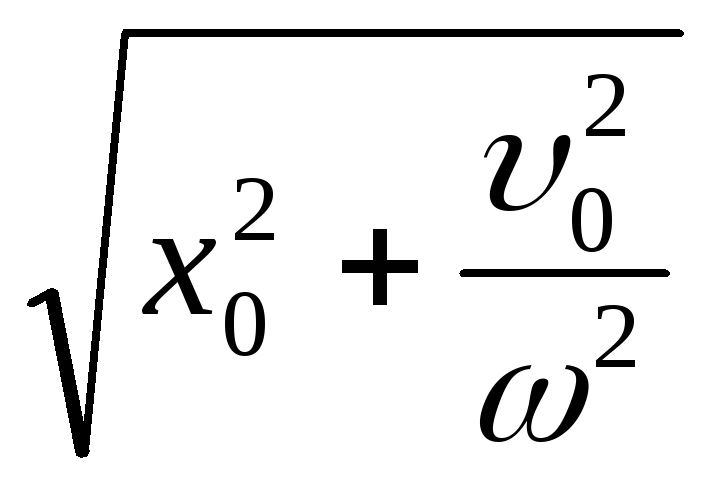cos  = звідки  = arc cos .

Числові значення амплітуди і початкової фази в одиницях умови задачі

A = =35,5 cм,

 = arc cos .

Скориставшись значеннями амплітуди коливань і початкової фази, знаходимо координату х і швидкість υ в момент часу t:

x = 35,5 cos (4  2,40 + /4) = - 20,2 см,

υ = - 35,5  4sin (4  2,40 + /4) = 115,7 см/с.

Відповідь: х = - 20,2 см; υ = 115,7 см/с.

Приклад 2. В результаті додавання двох гармонічних коливань однакового напрямку і близьких частот одержали результуюче рівняння x = A cos 2,1 t cos 50,0 t см. Визначити циклічні частоти коливань, які додаються, і період биття.

Дано:

x = A cos 2,1 t cos 50,0 t см

_______________________

₁ – ? ₂ – ? Т_б – ?

Розв’язування. Відомо, що при додаванні двох гармонічних коливань з близькими частотами ₁ і ₂ рівняння результуючого руху має вигляд:

х = .

Порівнюючи це рівняння і рівняння умови задачі, маємо

= 2,1 c^-1 i = 50,0 c^-1

Звідки ₁ = 47,9 c^-1; ₂ = 52,1 c^-1.

Періодичність зміни амплітуди визначається періодичністю зміни модуля косинуса:

T_б = ,

де Т_б – період биття.

Знаходимо період биття

T_б = = 1,49 с

Відповідь: ₁ = 47,9 с^-1; ₂ = 52,1 с^-1; Т_б = 1,49 с.

Приклад 3. Задаються рівняння руху частинки х = Аsin t і

y = В cos t, де А і В – амплітуди коливань частинки вздовж координатних осей х і y. Знайти: а) рівняння траєкторії частинки у(х) і напрям її руху вздовж цієї траєкторії; б) прискорення а в залежності від напряму радіуса вектора .

Дано:

х = Аsin t

y = В cos t

___________

у(х) – ? а – ?

Розв’язування. Рівняння траєкторії частинки одержимо, якщо рівняння (1) і (2) записати в такому вигляді:

sin t = , cost = .

Піднесемо до квадрата:

= sin²t; = cos² t;

Додавши ці рівняння одержимо:

+ =1 – еліпс.

Будуємо цю траєкторію в декартовій системі координат (рис.1):

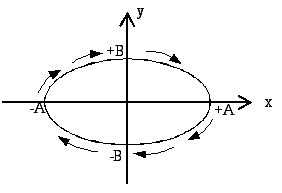
Рисунок 1

Аналізуючи рівняння умови задачі в різні моменти часу, знаходимо, напрям руху частинки вздовж траєкторії:

а) при t = 0, х = 0 і у = В – початок руху ;

б) при t = /4, х = А і у = 0 – наступна точка;

в) при t = T/2, х = 0 і у = -В і т. д.

Результуюче прискорення руху частинки визначаємо із відповідних прискорень руху вздовж осей х і у:

υ_х = А сos t; а_х= - А ² sin t = - ² x;

υ_y = - В  sin t; a_y= - В² cos t = - ² y;

.

Модуль вектора дорівнює

a = ² =² r ,

де – модуль радіуса-вектора частинки в довільний момент часу.

Радіус-вектор частинки завжди направлений від початку координат до положення точки на траєкторії. Вектор результуючого прискореннязавжди направлений від положення частинки на траєкторії руху до початку координат, тобто

.

Приклад 4. Однорідний стрижень поклали на два блоки, які швидко обертаються, як це показано на рис.2. Відстань між осями блоків l = 20 см, коефіцієнт тертя ковзання між стрижнем і блоками k = 0,18. Показати, що стрижень буде здійснювати гармонічні коливання. Знайти період цих коливань.

Дано: l = 20 см k = 0,18 ________ Т – ?

Рисунок 2

Розв’язування. При зміщенні стрижня вліво на величину х від положення рівноваги сили тертя F₁ i F₂, які виникають між стержнем і блоками дорівнюють

F₁ = F₂ =

де  – густина матеріалу стрижня;

S – переріз стрижня;

k – коефіцієнт тертя ковзання.

Повертаюча сила, яка виникне в цьому випадку, буде дорівнювати:

F = – (F₁ -F₂) = - 2  g S k x. (1)

За другим законом Ньютона ця ж сила дорівнює:

F = m a. (2)

Порівнюючи праві частини рівностей (1) і (2), маємо

ma + 2  g S k x = 0

aбо

x = 0 . (3)

Одержане диференціальне рівняння (3) є рівнянням гармонічних коливань. Циклічна частота цих коливань визначається співвідношенням:

² =

звідки

T = 2

або врахувавши, що m = lS, одержимо:

T = 2 .

Підставимо числові значення:

T = 6,28= 1,5 с.

Відповідь: Т = 1,5 с.

Приклад 5. Фізичний маятник у вигляді тонкого прямого стрижня довжиною 120 см коливається біля горизонтальної oсі, яка проходить перпендикулярно до стрижня через точку, віддалену на деяку відстань а від центра мас стрижня. При якому значенні а_е період коливань буде мати найменше значення? Знайти величину цього періоду?

Дано:

l = 120 см

_________

а_e – ?

Т_min – ?

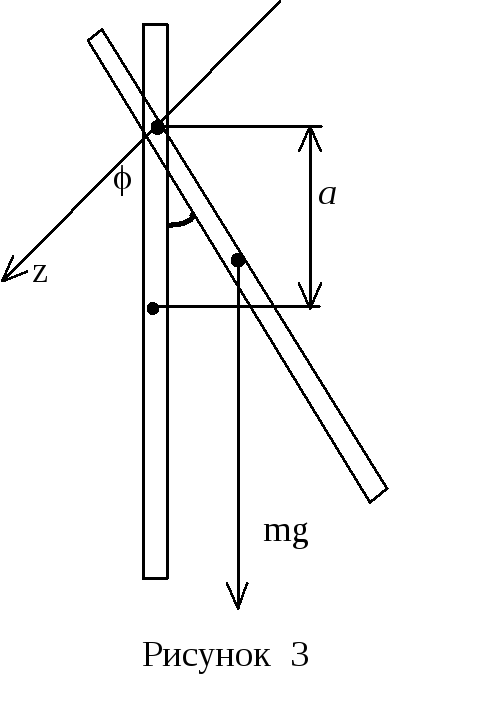
Розв’язування. Відведений від положення рівноваги стрижень буде здійснювати коливання відносно закріпленої осі, яка збігається з віссю Z (рис.3). Покажемо, що при малих кутах відхилення ( < 7), ці коливання будуть гармонічними. В будь-який момент часу на стрижень діють дві сили, сила тяжіння і сила реакції опори. Однак, обертаючий момент створюється лише силою тяжіння.

M =- mga sin , (1)

де а – відстань від осі обертання до центра мас стрижня;

 – кут відхилення стрижня від положення рівноваги.

Для малих кутів sin = , а напрям вектора протилежний до напрямку осіZ, тому

M_z = - mga  , (2)

Згідно з основним рівнянням динаміки обертального руху цей момент дорівнює:

M_z = І . (3)

Прирівняємо праві частини рівностей (2) і (3), одержимо:

I +mga  = 0.

Звідки:

= 0. (4)

Рівняння (4) є диференціальним рівнянням гармонічних коливань, квадрат циклічної частоти яких дорівнює:

(5)

де І – момент інерції стрижня відносно осі обертання;

а – відстань від точки підвісу до центра мас.

Момент інерції стрижня знайдемо за теоремою Штейнера згідно з якою:

I = I₀ + m a²,

де І₀ = ml² – момент інерції стрижня відносно осі, яка проходить через центр мас стрижня. Тому

І = m l² + ma² . (6)

Підставимо (6) в (5) і визначимо період коливань

T = 2 . (7)

Для визначення екстремальної відстані а_е від центра мас до точки підвісу, похідну за а підкореневого виразу формули (7) прирівняємо до нуля:

= 0 , .

Звідки

2 a² - - a² = 0;

a_e =  . (8)

a_e =  0,34 м.

Величину а_е з (8) підставимо в (7) і знайдемо значення найменшого періоду коливань фізичного маятника:

T_min = 2 =1,67 c.

Відповідь: а_е = 34 см; Т_min = 1,67 c.

Приклад 6. Кулька масою m і радіусом r котиться без ковзання по внутрішній поверхні циліндра радіусом R, виконуючи малі коливання біля положення рівноваги. Визначити період коливань кульки.

Рисунок 4

Розв’язування: На відведену від положення рівноваги кульку діють дві сили, сила тяжіння mg і сила реакції опори з точкою прикладання о₁. Обертаючий момент відносно миттєвої точки о₁ створюється лише силою тяжіння (рис.4.):

М = - mgr sin , (1)

де mg – сила тяжіння;

r – радіус кульки;

 – кут відхилення радіуса-вектора кульки від положення рівноваги.

У випадку, коли кут  < 7, sin  = . В цьому випадку

M = - mgr. (2)

За основним рівнянням динаміки обертального руху момент сили тяжіння дорівнює

М = І , (3)

де І – момент інерції кульки відносно миттєвої осі, яка проходить через точку о₁ ;

 – кутове прискорення кульки відносно точки о₁.

Прирівняємо праві частини рівностей (2) і (3):

I  + mgr  = 0. (4)

Момент інерції кульки відносно миттєвої осі знаходимо за теоремою Штейнера:

I = mr² + mr² = mr². (5)

Кутове прискорення кульки  можна визначити через дотичне прискорення а_ і радіус кульки r:

a_ =  r . (6)

Дотичне прискорення а_ також можна визначити відносно точки о циліндра:

a_ =  (R - r) , (7)

де  – кутове прискорення кульки відносно точки о, яке пов’язане із зміною кута повороту  за часом ( =  );

(R - r) – відстань від точки о до центра мас кульки.

Прирівняємо праві частини рівностей (6) і (7) і визначимо :

 = . (8)

Значення І з ( 5) і  з (8) підставимо в (4), одержимо:

+ mgr  = 0.

Звідки

= 0. (9)

Диференціальне рівняння (9) є рівнянням гармонічних коливань. Циклічна частота цих коливань дорівнює

 = .

Отже період коливань кульки:

T = 2 .

Приклад 7. Тіло масою 1 кг знаходиться у в’язкому середовищі з коефіцієнтом опору r = 0,05 кг/с. З допомогою двох однакових пружин жорсткістю k = 50 Н/м кожна тіло утримується в положенні рівноваги, пружини при цьому недеформовані. Тіло змістили від положення рівноваги, як це показано на рис.5, і відпустили. Визначити: а) коефіцієнт згасання ; б) частоту  коливань; в) логарифмічний декремент коливань δ; г) число N коливань за час, протягом якого амплітуда коливань зменшиться в е разів; д) добротність коливальної системи.

Д

ано:

m = 1 кг

r = 0,05 кг/с

k = 50 Н/м

_____________

 – ?  – ? δ – ?

N – ?  – ?

Рисунок 5

Розв’язування. На відведене від положення рівноваги тіло (рис.5) діють дві однакові сили F₁ = F₂ = kx, які направлені в один бік. Повертальна сила в цьому випадку дорівнює:

F_n = - 2kx. (1)

При русі тіла у в’язкому середовищі з боку останнього виникає сила опору, яка пропорційна швидкості руху тіла:

F₀ = - r .(2)

Інших сил в напрямі руху тіла при здійсненні коливань не існує. За другим законом Ньютона результуюча цих двох сил призводить до виникнення прискорення, тобто можна записати:

(3)

Рівняння (3) можна перетворити:

= 0, (4)

де =2,  – коефіцієнт згасання;

= ₀², ₀ – власна циклічна частота.

З урахуванням позначень рівняння (4) набуде вигляду:

= 0. (5)

Рівняння (5) є диференціальним рівнянням згасаючих коливань, розв’язком якого є функція:

x = A₀ e^-t cos (t + ). (6)

Розв’язування: а) коефіцієнт згасання дорівнює

 = = 0,025 c^-1;

б) частоту коливань  знайдемо за формулою:

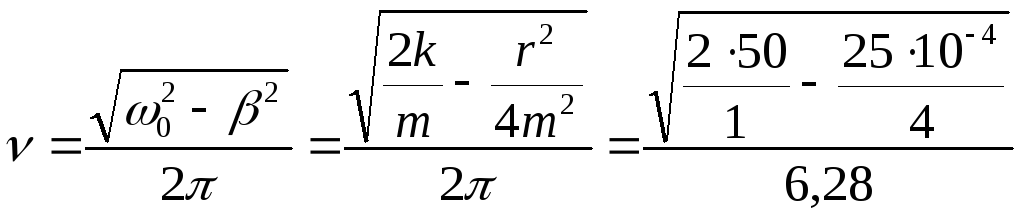= 1,59 c^-1;

в) логарифмічний декремент згасання дорівнює

δ = ln =0,0157;

г) число коливань, які виконані коливальною системою за час , протягом якого амплітуда зменшиться в е разів, дорівнює

N = ,

де  – час, за який амплітуда зменшується в e paзів;

Т – період згасаючих коливань.

Спочатку знайдемо час 

1 = ln =  ,

звідки

 = .

Тоді

N =

д) добротність коливальної системи

= 200.

Відповідь:  = 1,59 с^-1; δ= 0,0157; N = 64;  = 200.

Приклад 8. Частинку змістили від положення рівноваги на відстань А₀ = 1 см і відпустили. Який шлях пройде ця частинка, здійснюючи згасаючі коливання, до повної зупинки, якщо логарифмічний декремент згасання δ = 0,01 ?

Дано:

А₀ = 1 см

δ = 0,01

_________

S – ?

Розв’язування. Зміщена від положення рівноваги частинка за першу чверть періоду, після того, як її відпустили, пройде шлях S₁ = A_0. За кожну наступну половину періоду частинка буде проходити відповідно шляхи

S₂ =2A₀ ; S₃ = 2A₀ ; S₄ = 2 A₀  i т.д.

Весь шлях руху частинки буде дорівнювати

S = S₁ + S₂ + S₃ +....+ S_n.

Або

S = А₀ + 2А₀ + 2А₀ + 2А₀ +...+ 2А₀ .

Після спрощення одержимо

S = A₀  .

В круглих дужках нескінченно спадна геометрична прогресія, сума членів якої визначається за формулою

S_n = ,

де а₁ = – перший член геометричної прогресії;

q = – знаменник прогресії.

Тому

S = A₀  .

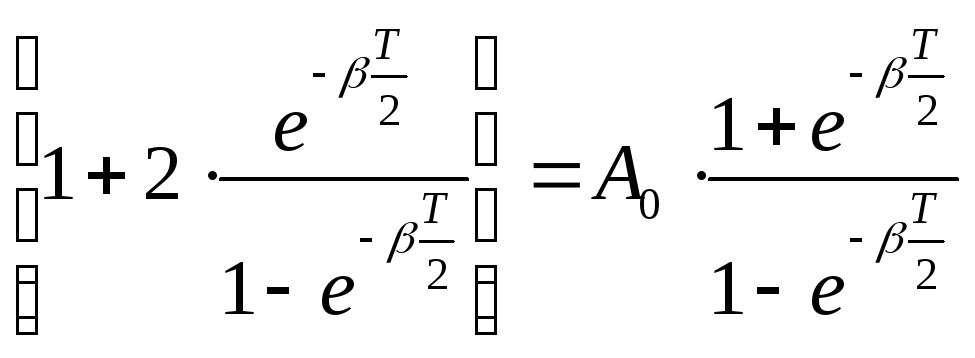Врахувавши те, що Т =δ, одержимо

S = 0,01  = 4 м

Відповідь: S = 4 м.

Приклад 9. До спіральної пружини жорсткістю 10 Н/м підвісили тягарець масою 10 г і занурили всю систему у в’язке середовище. Прийнявши коефіцієнт опору середовища рівним 0,1 кг/с, визначити: а) частоту ₀ власних коливань; б) резонансну частоту _рез; в) резонансну амплітуду А_рез, якщо вимушувальна сила змінюється за гармонічним законом і її амплітудне значення F₀ = 0,02 Н; г) відношення резонансної амплітуди до статичного зміщення пiд дією сили F₀.

Дано:

k = 10 Н/м

m = 10 г

r = 0,1 кг/с

____________________

₀ – ? _рез – ? А_рез – ? – ?

Аналіз теорії задачі. На тягарець, який здійснює коливання, окрім сили тертя і пружної сили, діє зовнішня сила, яка змінюється за гармонічним законом. З урахуванням дії всіх сил диференціальне рівняння коливань матиме вигляд:

m+ r+ kx = F₀ cos  t. (1)

Поділимо рівняння (1) на масу тягарця m і введемо позначення:

; ;, одержимо

+ 2 +₀² x = f cos t. (2)

Рівняння (2) є неоднорідним лінійним диференціальним рівнянням другого порядку. Рoзв’язком такого рівняння є функція, яка складається з двох частин:

x = A₀e^-t cos(t + ) + A cos (t + ) . (3)

Через деякий час під дією вимушувальної сили коливання тягарця стануть стабільними. Тому розв’язком рівняння (2) буде лише функція

x = A cos (t + ). (4)

Першу та другу похідні від (4) підставимо в (2):

= - A sin (t + ) = Acos (t +  + /2),

= - A² cos (t + ) = A² cos (t +  + ) ,

A² cos (t +  + ) + 2  A cos (t +  + /2) +

+ A² cos (t + ) = f₀ cos t. (5)

Введемо позначення: А₁ = A²; A₂ = 2  A; A₃ = A ₀²; A₄ = f₀.

Для знаходження амплітуди А вимушених коливань скористаємось векторною діаграмою, на якій відкладемо амплітуди А₁, А₂, А₃, А₄ згідно з (5) (рис.6)

A₄² = A₂² + (A₃ - A₁)²

або врахувавши позначення, одержимо:

f₀² = 4² A² ² + (₀² - ²) A².

Звідки маємо: Рисунок 6

A = . (6)

Аналіз виразу (6) амплітуди вимушених коливань:

а)  << ₀, тобто   0

A_ст =, (7)

де А_ст – статичне зміщення тягарця під дією сталої сили F₀;

б)   ₀

A_р = , (8)

де А_р – резонансне значення амплітуди (при   0, А_p  ).

Для знаходження резонансної частоти і резонансної амплітуди дослідимо на максимум підкореневий вираз формули (6):

= 0 .

Звідки

_р = , (9)

де _р – резонансна частота вимушених коливань.

Значення _р з (9) підставимо в (6)

A_р = . (10)

Якщо   0, то A_р = , що збігається з формулою (8).

Розв’язування: а) частота ₀ власних коливань тягарця дорівнює

₀ = =5,03 c^-1;

б) резонансна частота знаходиться за формулою (9)

_р =

= 4,91 c^-1 ;

в) резонансну амплітуду знайдемо за формулою (10)

A_рез = =6,4  10^-3 м;

г) відношення резонансної амплітуди до статичного зміщення тягарця, тобто добротність коливальної системи, дорівнює

= = 160.

Відповідь: ₀ = 5,03 с^-1; _р = 4,91 с^-1; А_р = 6,4 мм;  = 160.