2.2. Другий закон Ньютона. Рівняння руху точки

Другий закон Ньютона є основним законом динаміки. Він виконується лише в інерційних системах відліку. Це фундаментальний закон природи, которий є узагальненням багатьох дослідних фактів. Формулюється другий закон Ньютона так:

Прискорення, набуте матеріальною точкою або тілом, пропорційне рівнодійній всіх діючих сил і обернено пропорційне масі матеріальної точки або тіла.

, або . (2.2.1)

Більш загальне формулювання другого закону Ньютона таке:

Швидкість зміни імпульсу тіла дорівнює діючій на нього силі.

. (2.2.2)

Векторна величина називається елементарним імпульсом сили. Згідно з другим законом Ньютона зміна імпульсу матеріальної точки або тіла дорівнює імпульсу діючої на точку або тіло сили, тобто

. (2.2.3)

Основний закон динаміки матеріальної точки виражає принцип причинностів класичній механіці. Суть цього принципу визначає однозначний зв’язок між зміною в часі стану руху і положення в просторі матеріальної точки або тіла і діючої сили. Це дозволяє використати початкові умови стану матеріальної точки та розрахувати її стан в довільний наступний момент часу.

Другий закон Ньютона, записаний у вигляді

, (2.2.4)

називається рівнянням руху точки. Така форма запису другого закону Ньютона використовується для розв’язування задач стосовно матеріальної точки або твердого тіла.

У механіці велике значення має принцип незалежної дії сил. Якщо на матеріальну точку діють одночасно кілька сил, то кожна з них надає матеріальній точці прискорення у відповідності з другим законом Ньютона. Згідно з цим принципом сили й прискорення можна проектувати на координатні осі, що суттєво полегшує розв’язування задач.

Дотичне (тангенціальне) й нормальне (доцентрове) прискорення матеріальної точки або твердого тіла, можна визначати за допомогою відповідних складових сил:

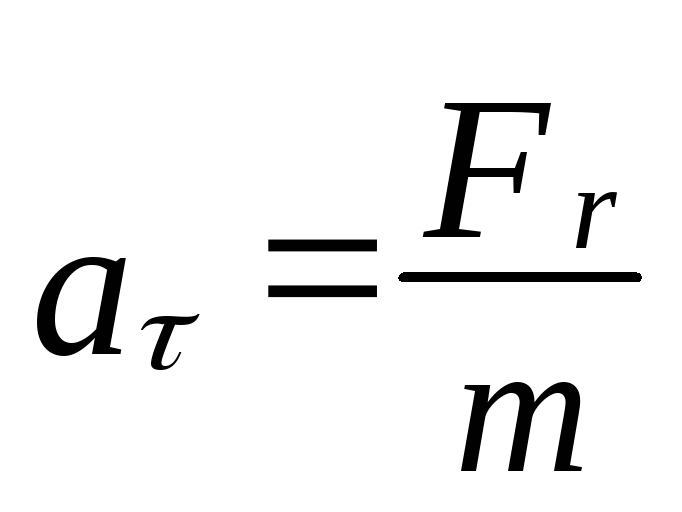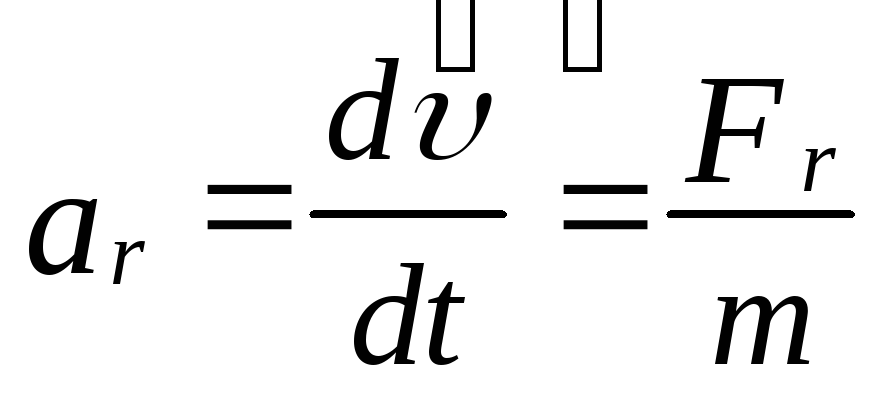; ;, (2.2.5)

а також

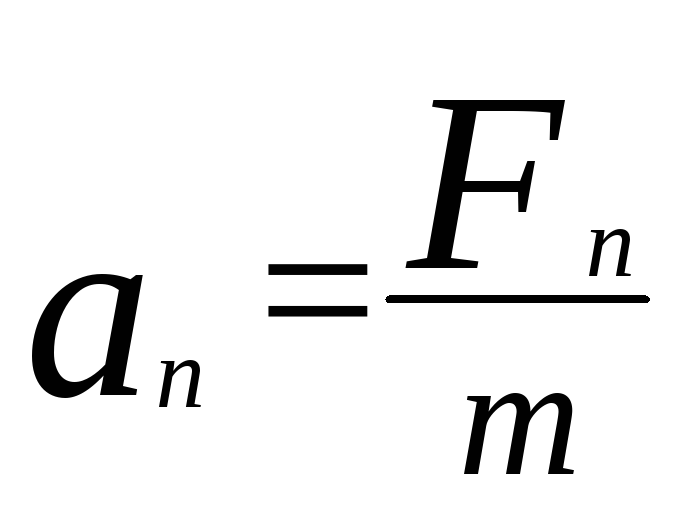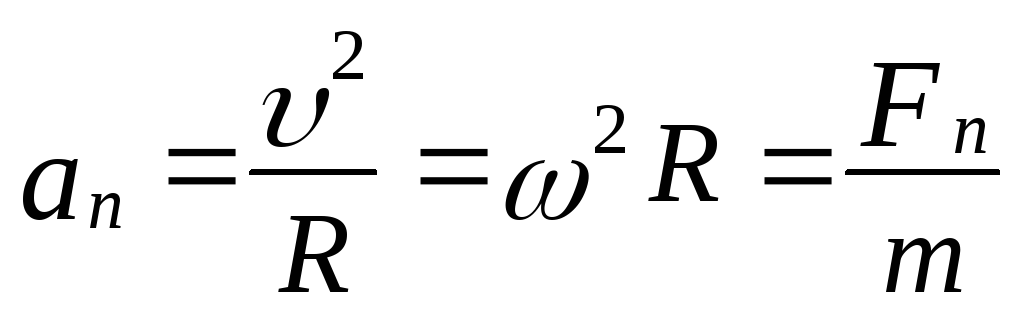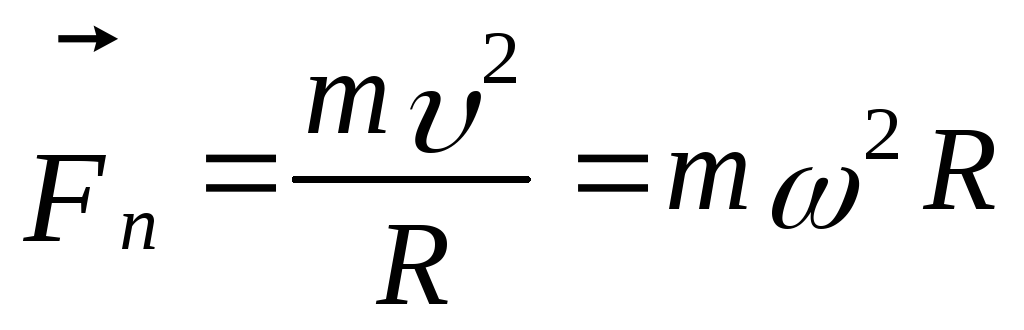; ;, (2.2.6)

де - дотична складова діючої сили;- нормальна складова сили.

Короткі висновки:

• другий закон Ньютона є експериментальним законом. Він виник у результаті оброблення величезної кількості експериментальних фактів;

• у випадку, коли результуюча всіх діючих сил = 0, тобто при відсутності дії на тіло інших тіл, прискорення з яким рухається тіло теж буде дорівнювати нулю. Цей висновок збігається з першим законом Ньютона, тому можна вважати, що перший закон Ньютона є окремим випадком другого закону.

2.3. Третій закон Ньютона. Закон збереження імпульсу

Сили, з якими взаємодіють тіла або матеріальні точки, завжди рівні за модулем й протилежні за напрямком.

Це і є формулювання третього закону Ньютона.

Результатом третього закону Ньютона є ствердження того, що сили взаємодії направлені уздовж прямої, яка з’єднує взаємодіючі тіла або матеріальні точки, тобто

. (2.3.1)

У співвідношенні (2.3.1) сили іприкладені до різних тіл, а тому не можуть зрівноважувати одна одну. Додавати за правилом векторного додавання можна лише сили, прикладені до одного тіла. Сили, прикладені до різних матеріальних точок (тіл), завжди діють парами і є силами однієї природи.

Третій закон Ньютона дозволяє перейти від динаміки окремої матеріальної точки до динаміки системи матеріальних точок, оскільки дозволяє звести будь-яку взаємодію до сил парної взаємодії між цими матеріальними точками.

Доведемо що в довільній замкненій системі сумарний імпульс всіх матеріальних точок або тіл цієї системи з часом не змінюється (закон збереження імпульсу).

Розглянемо механічну систему, яка складається із n матеріальних точок або тіл, маси і швидкості яких відповідно дорівнюють m₁, m_2,m_3,… m_nі,,,...

Запишемо другий закон Ньютона для кожного із тіл (матеріальних точок) цієї системи:

,

. . . . . . . . . . . .

, (2.3.1)

де - рівнодійні всіх внутрішніх сил, діючих на відповідні тіла або матеріальні точки системи;- рівнодійні всіх зовнішніх сил.

Додамо почленно ці рівняння, одержимо:

. (2.3.2)

або

. (2.3.3)

У відповідності з третім законом Ньютона всі внутрішні сили мають парний характер, а тому взаємно компенсують одна одну

. (2.3.4)

Для замкненої механічної системи , зовнішні сили на тіла ізольованої системи не діють. Тому

,

звідки

. (2.3.5)

Вираз (2.3.5) є законом збереження імпульсу в механіці.

У відповідності з законом збереження імпульсу відбувається рух ракет, взаємодіють між собою матеріальні точки або тверді тіла тощо.

Короткі висновки:

• при відсутності дії зовнішніх сил сумарний імпульс усіх тіл замкнутої системи з часом не змінюється. (наслідок закону збереження імпульсу);

• сумарний імпульс залишається сталим і для незамкнутої системи при умові, що зовнішні сили в сумі не дорівнюють нулю. Однак і в цьому випадку проекції суми цих сил на відповідні напрямки мають дорівнювати нулю.

В класичній механіці Ньютона через те, що маса тіла не залежить від швидкості руху (v << c), імпульс системи тіл може бути виражений через швидкість її центра мас.

Центром мас (або центром інерції) системи матеріальних точок називається деяка точка в тілі або системі матеріальних точок, положення якої характеризує розподіл маси цієї системи.

Радіус-вектор центра мас системи матеріальних точок або твердих тіл (рис. 2.1.) дорівнює

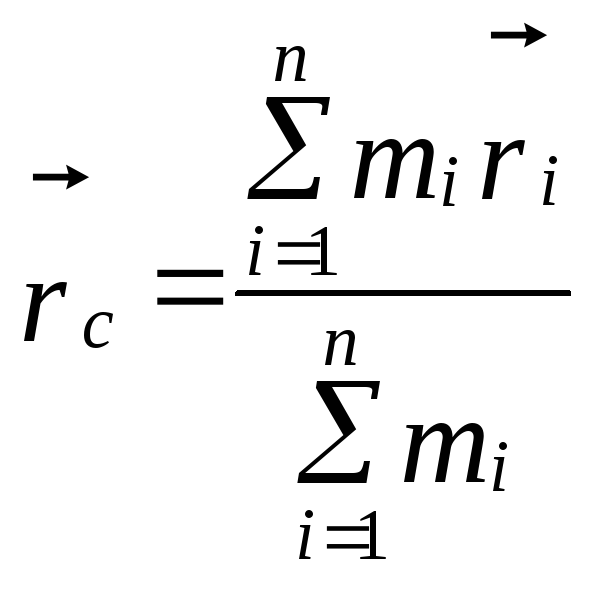, (2.3.6)

де і- маса і радіус-вектор і -ї точки в системі;- сумарна маса всіх тіл або матеріальних точок системи.

У цьому випадку імпульс системи матеріальних точок визначається формулою:

. (2.3.7)

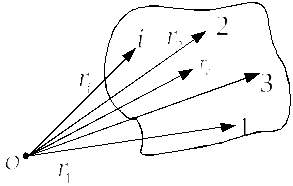
Рис.2.1.

Центр мас системи рухається як матеріальна точка, в якій зосереджена маса всієї системи. Рівняння руху центра мас системи можна записати так:

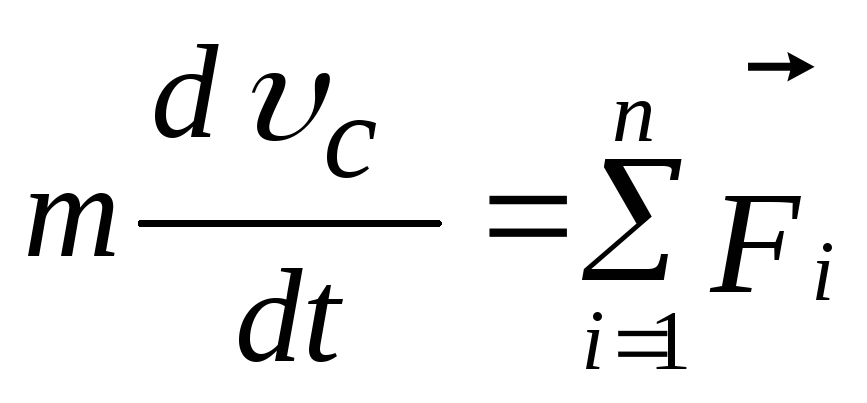. (2.3.8)

Із закону збереження імпульсу витікає, що центр мас замкнутої системи або рухається рівномірно й прямолінійно, або залишається в стані спокою.

Зупинимося коротко на характеристиці сил, які діють в механіці.

В системі відліку зв’язаною із Землею, на будь-яке тіло масою m діє сила тяжіння.

, (2.3.9)

де – прискорення сили земного тяжіння. Біля поверхні землі g=9,81 м/с². Сили тяжіння діють на всі тіла. Не завжди сила тяжіння може бутивагою тіла.

Вага тіла– це сила, з якою тіло діє внаслідок тяжіння на опору або підвіс. Вага тіла може дорівнювати силі тяжіння лише у випадку перебування його в стані спокою на горизонтальній підставці (рис. 2.2)

Вага тіла чисельно дорівнює реакції опори, однак направлена по лінії дії сили тяжіння.

. (2.3.10)

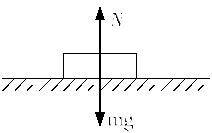
Рис.2.2.

В усіх інших випадках вага тіла не дорівнює силі тяжіння.

Невагомість – це стан тіла, при якому воно рухається тільки під дією сили тяжіння. Будь-яке вільно падаюче тіло перебуває завжди в стані невагомості.

Крім гравітаційних сил широко поширені сили пружності, які проявляються при взаємодії тіл у виглядідеформацій.

В межах пружності тіл пружні сили, як правило, пропорційні величині деформацій

, (2.3.11)

де - величина деформації; k - коефіцієнт пружності, різний для різних тіл.

Природа пружних сил пов’язана з електромагнітними взаємодія-ми.

Сили тертявиникають при ковзанні одних тіл по поверхні інших тіл. У цьому випадку сила тертя пропорційна силі нормального тиску, тобто

_тер = k·, (2.3.12)

де k – коефіцієнт тертя (залежить від оброблення поверхонь ковзання); N – сила нормального тиску.

Сила тертя завжди перешкоджає направленому руху тіла. Природа сили тертя теж пов’язана із електромагнітними взаємодіями.