
- •С.Г.Авдєєв, т.І.Бабюк
- •Лекція 1
- •1.2. Рух точки по колу. Кутова швидкість і кутове прискорення
- •1.3. Тангенціальне й нормальне прискорення. Зв’язок між кінематичними величинами криволінійного руху
- •Лекція 2
- •2.2. Другий закон Ньютона. Рівняння руху точки
- •2.3. Третій закон Ньютона. Закон збереження імпульсу
- •Лекція 3
- •3.2. Консервативні й неконсервативні сили. Потенціальна енергія. Зв’язок роботи й потенціальної енергії
- •Знайдемо роботу переміщення матеріальної точки з положення м1 в положення м2. Для цього спочатку знайдемо роботу переміщення точки (тіла) з точки “м1” в точку “о” і з точки “м2” в точку “о”.
- •3.3.Сила й потенціальна енергія. Поняття градієнта
- •3.4. Закон збереження й перетворення механічної енергії
- •Лекція 4
- •4.2. Моменти інерції найпростіших тіл: диск, стержень, куля.
- •4.4. Закон збереження моменту імпульсу і його використання. Гіроскопи. Гіроскопічний ефект
- •Лекція 5
- •5.2. Наслідки перетворення координат Лоренца.
- •5.3. Зв’язок маси і енергії
- •Лекція 6
- •6.2. Електричне поле і його напруженість. Принцип суперпозиції полів. Поле точкового заряду
- •6.3. Теорема Гаусса і її використання
- •З рисунка видно, що
- •За теоремою Гаусса
- •7.2. Потенціал електростатичного поля. Різниця потенціалів. Принцип суперпозиції
- •7.3. Зв’язок між потенціалом і напруженістю електростатич-ного поля. Приклади розрахунку полів
- •Рис 7.5
- •Лекція 8
- •8.2. Електроємність окремого провідника. Конденсатори. Ємність конденсаторів різної форми
- •8.3. Енергія взаємодії електричних зарядів. Енергія окремого провідника і конденсатора
- •8.4. Енергія електростатичного поля. Густина енергії електро-статичного поля
- •Лекція 9
- •9.2. Вектор електричного зміщення. Теорема Гаусса для поля в
- •Лекція 10
- •Струм і існує у зовнішній ділянці кола і створюється полем . Струміснує у джерелі і створюється полем сторонніх сил.
- •10.2. Закон Джоуля-Ленца в інтегральній формі. Опір провідників. Потужність струму
- •10.3. Закони Ома для ділянки кола, неоднорідної ділянки кола й замкнутого кола. Правила Кірхгофа
- •10.4. Закони Ома й Джоуля-Ленца в диференціальній формі. Густина електричного струму в провіднику
- •Лекція 11
- •11.2. Закон Біо-Савара-Лапласа та його використання у найпростіших випадках
- •Лекція 12
- •12.2. Ефект Холла. Магнетогазодинамічний генератор та його використання
- •12.3. Явище електромагнетної індукції
- •12.4. Самоіндукція. Індуктивність. Е.Р.С. Самоіндукції
- •Лекція 13
- •13.2. Магнетний потік. Теорема Гаусса для магнетного поля
- •13.3. Робота переміщення провідника із струмом і контуру із струмом у магнетному полі
- •13.4. Енергія магнетного поля
- •Лекція 14
- •Розглянемо цей випадок трохи детальніше. Скористаємось другим законом Ньютона
- •14.2. Магнетна сприйнятливість і проникність
- •14.3. Циркуляція намагнечування. Вектор напруженості магнетного поля
- •14.4. Феромагнетики та їх основні властивості
- •Д о д а т о к Програма першої частини
- •Плани практичних занять
- •Графік виконання лабораторних робіт
- •Контрольні запитання для захисту лабораторних робіт
- •Тренувальні варіанти контрольної роботи 1 Варіант 1
- •Варіант 2
- •Варіант 3
- •Колоквіум 1
Розглянемо цей випадок трохи детальніше. Скористаємось другим законом Ньютона
![]() ,
(14.1.6)
,
(14.1.6)
де
![]() - електрична сила індукована змінним в
часі магнетним полем;m– маса електрона;
- електрична сила індукована змінним в
часі магнетним полем;m– маса електрона;![]() - прискорення гальмування.
- прискорення гальмування.
З рівняння (14.1.6) прискорення руху електрона дорівнює
![]() .
(14.1.7)
.
(14.1.7)
Напруженість вихрового електричного поля Е знайдемо з рівняння Максвелла (14.1.5)
![]() ,
,
де
![]()
![]() ,
а
,
а![]() ,
тому
,
тому![]() ,
звідки
,
звідки![]() .
.
Тому
![]() ,
або
,
або![]() .
.
Інтегруємо останній вираз у межах зміни швидкості відодо , а індукції магнетного поля від 0 до В
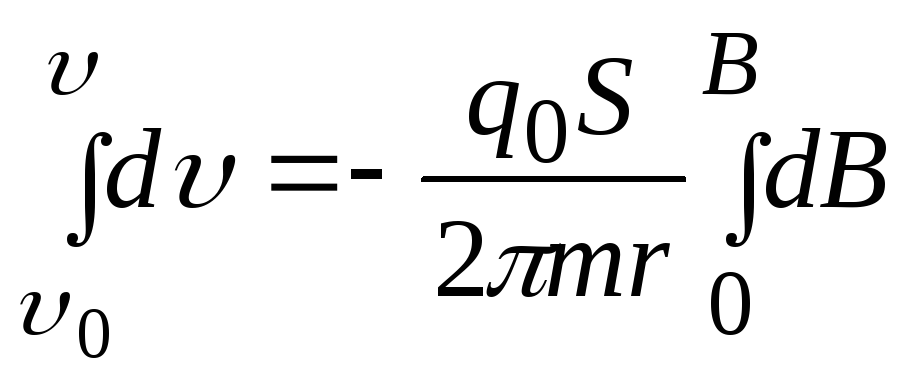 .
.
Після інтегрування одержимо:
![]() .
(14.1.8)
.
(14.1.8)
Значення швидкості з (14.1.8) підставимо у вираз орбітального магнетного моменту (14.1.3)
![]() .
(14.1.9)
.
(14.1.9)
Для атома, в якому є zелектронів, одержимо:
![]() ,
(14.1.10)
,
(14.1.10)
де
![]() - складова, яка пов’язана з орбітальним
рухом електрона в атомі;
- складова, яка пов’язана з орбітальним
рухом електрона в атомі;![]() - складова, яка появляється лише у
зовнішньому магнетному полі.
- складова, яка появляється лише у
зовнішньому магнетному полі.
Одержана формула (14.1.10) показує, що магнетний момент атома у випадку дії змінного в часі магнетного поля зменшується за рахунок намагнечування атома у протилежному напрямі.
Магнетики, для яких характерна ця особливість, називаються діамагнетиками.
Покажемо, що у
випадку, коли
![]() не збігається з напрямком дії змінного
в часі магнетного поля, такі атоми
здійснюють прецесію. Частота цієї
прецесії дорівнює
не збігається з напрямком дії змінного
в часі магнетного поля, такі атоми
здійснюють прецесію. Частота цієї
прецесії дорівнює
![]() ;
;
але
![]() ,
тому
,
тому
![]() ,
де
,
де
![]() .
.
Величину
![]() - називають гіромагнетним відношенням,
а
- називають гіромагнетним відношенням,
а![]() - Ларморова частота прецесії.
- Ларморова частота прецесії.
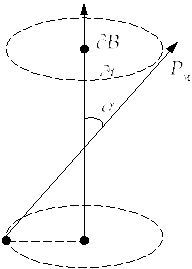
Рис.14.3
14.2. Магнетна сприйнятливість і проникність
Якщо магнетики
намагнечуються у ту ж сторону, що і
![]() ,
то вони називаютьсяпарамагнетиками.
,
то вони називаютьсяпарамагнетиками.
Кількісною мірою намагнечування є вектор намагнеченості, який можна подати через одиницю об’єму речовини:
![]() ,
(14.2.1)
,
(14.2.1)
де n– концентрація атомів або їх число в
одиниці об’єму магнетика;![]() - індукований магнетний момент атома,
друга складова у рівнянні (14.1.10).
- індукований магнетний момент атома,
друга складова у рівнянні (14.1.10).
З урахуванням викладеного одержуємо
![]() ,
,
або
![]() .
(14.2.2)
.
(14.2.2)
Величину ![]() називають магнетною сприйнятли-вістю.
називають магнетною сприйнятли-вістю.
Якщо магнетна сприйнятливість <0, то такі магнетики називаютьдіамагнетиками.
За розрахунками Кюрі-Венса для парамагнетиків
![]() .
.
У цьому випадку магнетна сприйнятливість обернено пропорційна до абсолютної температури.
З інших міркувань встановлено, що
![]() ,(14.2.3)
,(14.2.3)
де - відносна магнетна проникність середовища;- магнетна сприйнятливість.
Із співвідношення (14.2.3) одержуємо:
> 1- парамагнетики; < 1 - діамагнетики.
Прикладом діамагнетних речовин є металевий вісмут. При внесенні шматочка вісмуту, підвішеного до нитки у зовнішнє магнетне поле, останнє цей шматочок виштовхує з магнетного поля.
Парамагнітна мідь або латунь слабо втягуються у зовнішнє магнетне поле.
14.3. Циркуляція намагнечування. Вектор напруженості магнетного поля
Нехай у деякому середовищі діє зовнішнє магнетне поле, напрям якого показаний на рис. 14.4
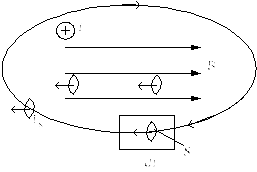
Рис.14. 4
Замкнутий контур, показаний на рис.14.4, охоплює певну кількість атомних струмів іk, а також струм провідностіІ.
Знайдемо циркуляцію
вектора
![]() вздовж замкнутого контуру
вздовж замкнутого контуру
![]() ,
(14.3.1)
,
(14.3.1)
де І – струм
провідності;
![]() - алгебраїчна сума всіх атомних струмів,
нанизаних на цей контур.
- алгебраїчна сума всіх атомних струмів,
нанизаних на цей контур.
Виділимо об’єм Sdl, у якому міститьсяidNелементарних атомних струмів. У виділеному об’ємі
![]() ,
(14.3.2)
,
(14.3.2)
де j –вектор намагнеченості магнетика.
З урахуванням (14.3.2) алгебраїчну суму всіх атомних струмів можна записати так:
![]() . (14.3.3)
. (14.3.3)
Закон повного струму (14.3.1) з урахуванням останніх зауважень буде мати вигляд:
![]() ;
(14.3.4)
;
(14.3.4)
або
![]() , (14.3.5)
, (14.3.5)
де
![]() =Н
– напруженість магнетного поля.
=Н
– напруженість магнетного поля.
З урахуванням цього позначення закон повного струму набуде вигляду:
![]() (14.3.6)
(14.3.6)
Оскільки вектор намагнечування магнетика визначається через магнетну сприйнятливість і напруженість магнетного поля співвідно-шенням (14.2.2)
![]() ,
,
то індукція магнетного поля буде дорівнювати
![]() ,
,
або
![]() .
(14.3.7)
.
(14.3.7)
Введемо позначення
![]() ,
тоді
,
тоді
![]() ,
,
де ![]() відносна магнетна проникність середовища;0– магнетна
проникність вакууму.
відносна магнетна проникність середовища;0– магнетна
проникність вакууму.
Оскільки
![]() ,
а
,
а![]() ,
то
,
то
![]() . (14.3.8)
. (14.3.8)
Графічно цю залежність виражають так:
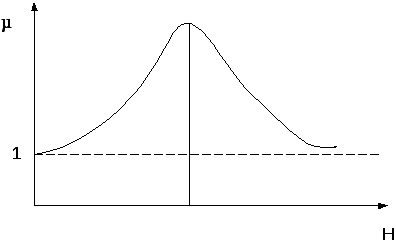
Рис.14.5
Всі магнетики діляться на три групи, для яких:
![]() - діамагнетики;
- діамагнетики;
![]() - парамагнетики;
- парамагнетики;
>>0; >> 1 – феромагнетики.
