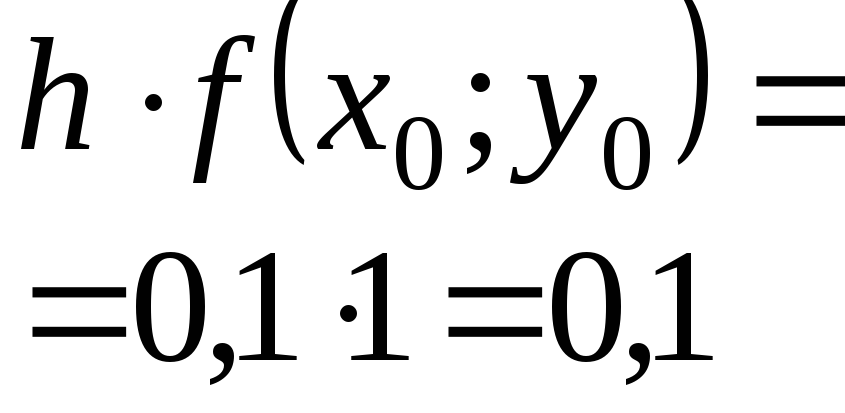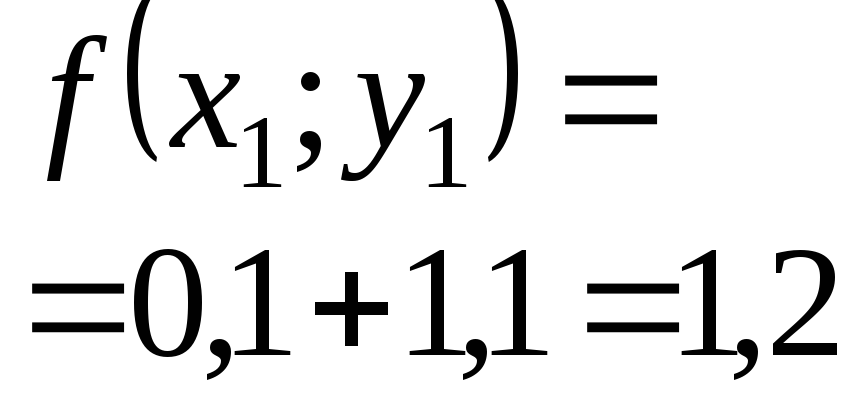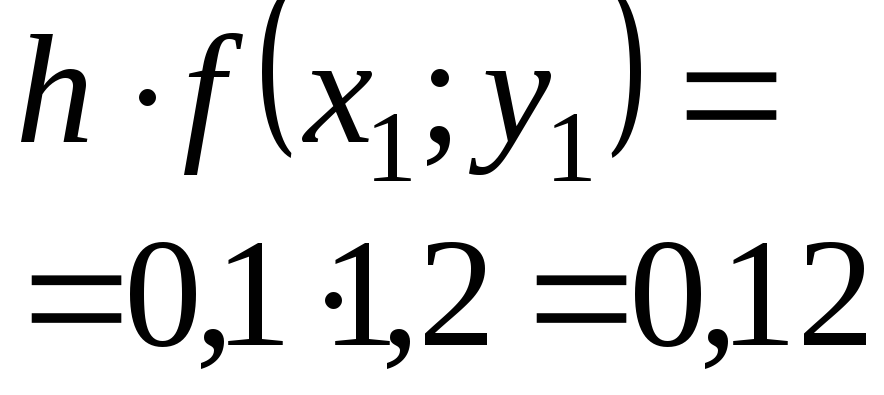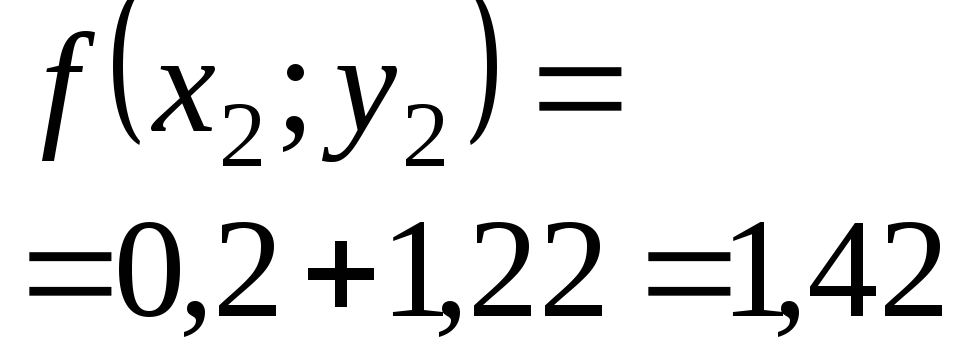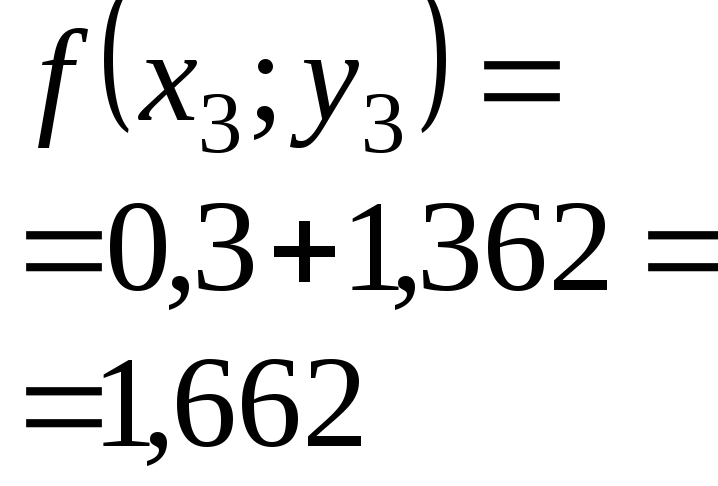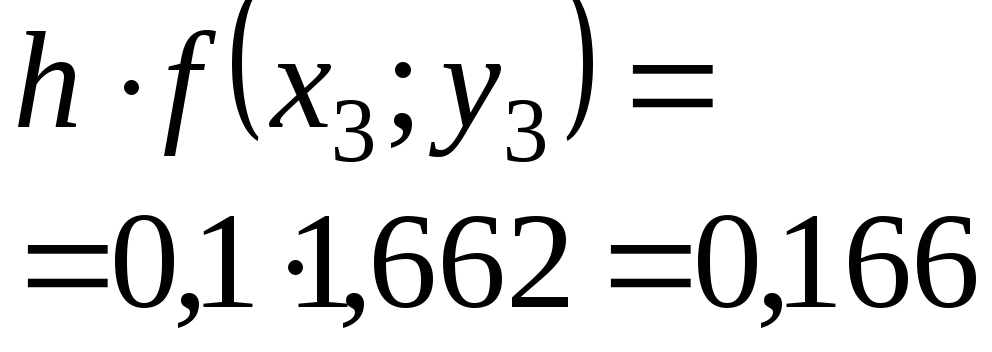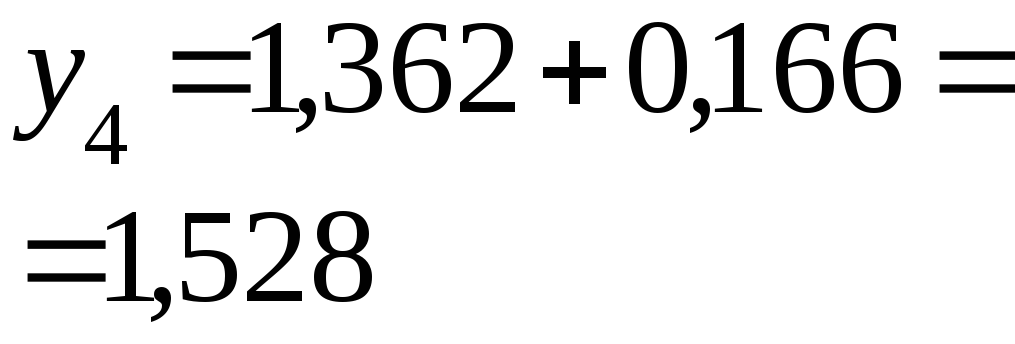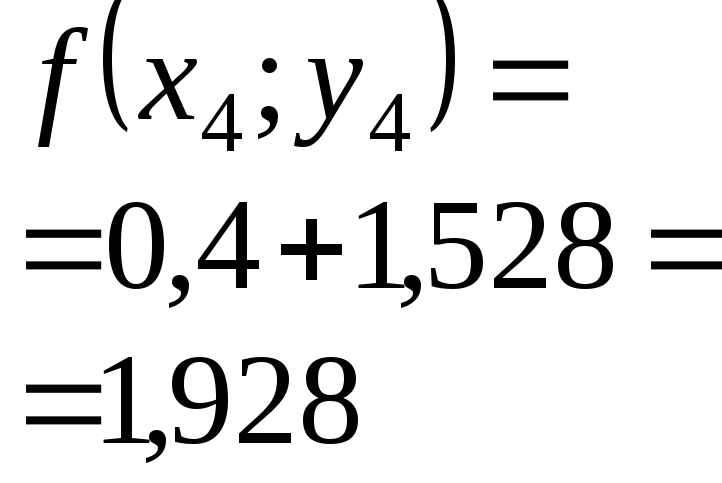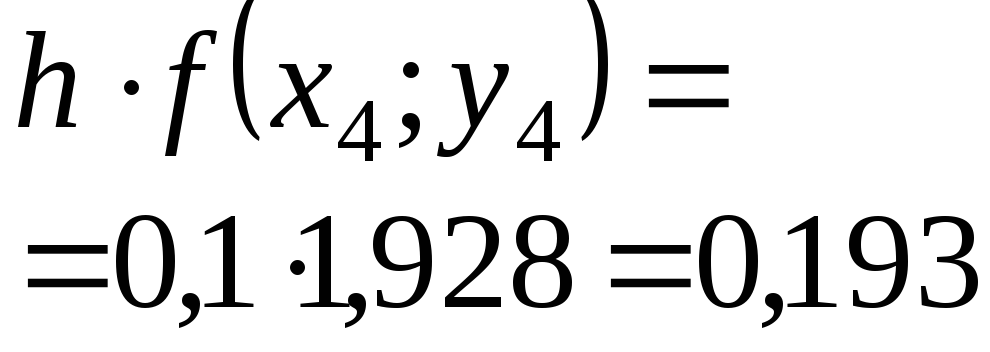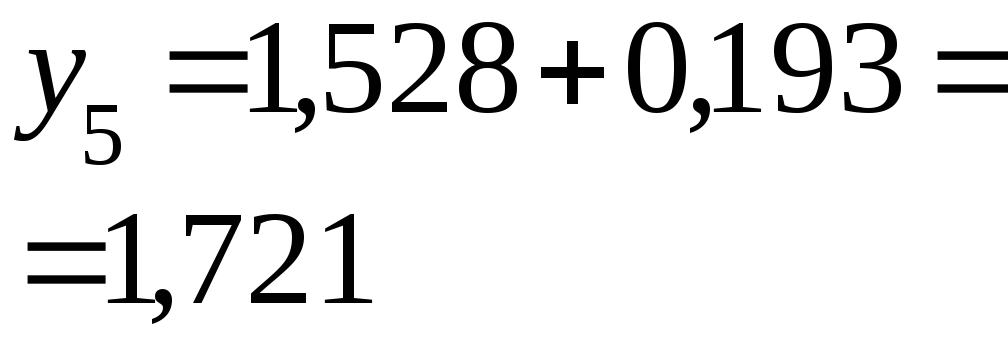Образец выполнения ргр

Задание. Найти решение дифференциального уравнения с начальным условием на отрезке , приняв за шаг .

1. Точное решение

- линейное уравнение.

Подстановка:

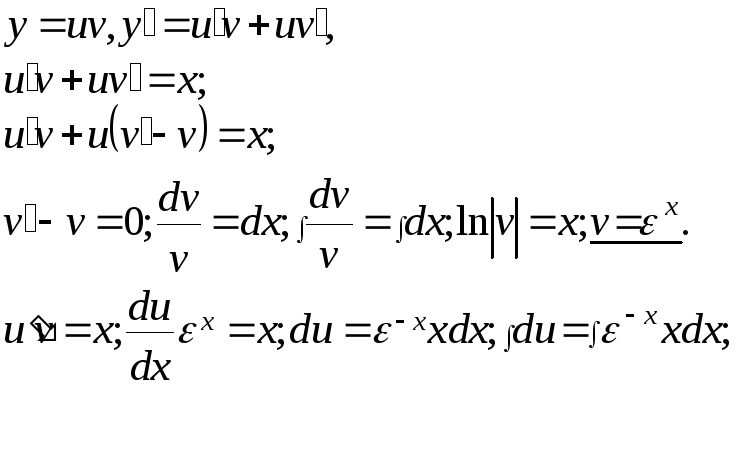
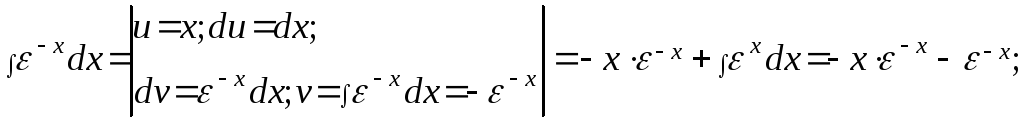
При найдем

- точное решение дифференциального уравнения.

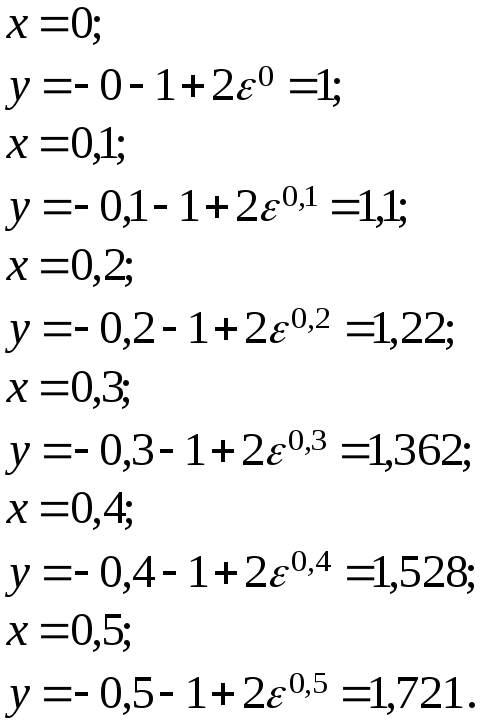
2. Приближенное решение дифференциального уравнения по методу Эйлера.

Т.к. то

0
1
2
3
4
5

3. Приближенное решение дифференциального уравнения по методу Рунге-Кутта

1) Записываем в первой строке

2) Вычисляем тогда

3) Записываем во второй строке:

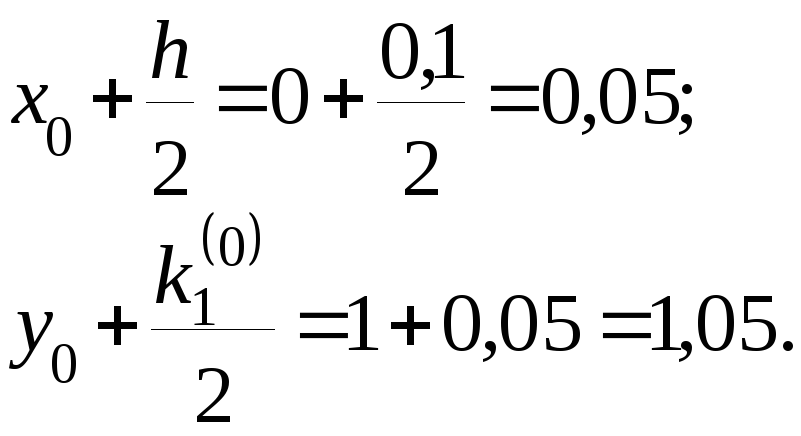
4) Вычисляем 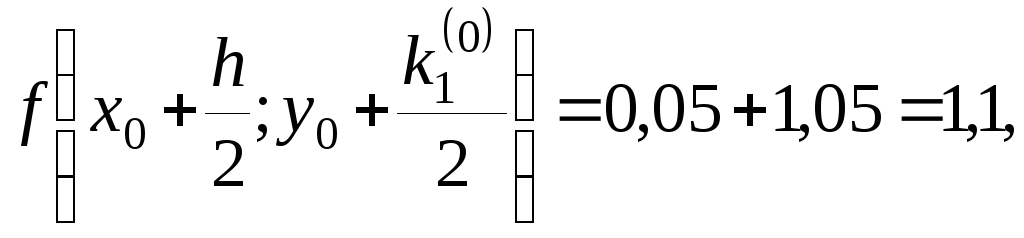тогда

5) Записываем в третьей строке

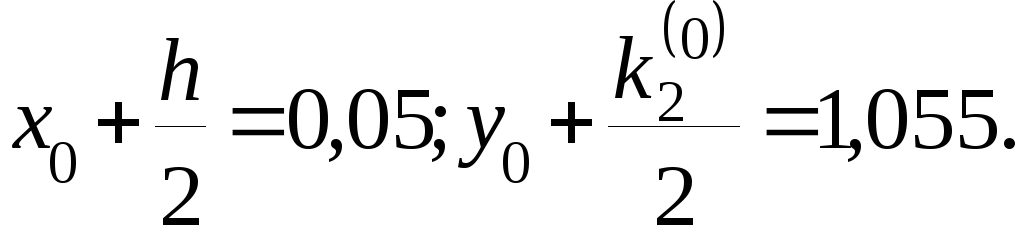
6) Вычисляем 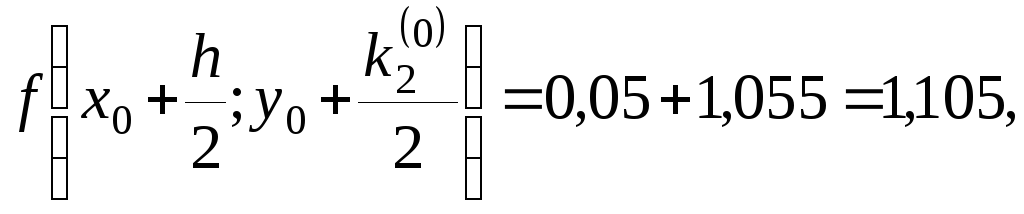тогда

7) Записываем в четвертой строке

8) Вычисляем тогда

9) В столбце записываем

10) Вычисляем

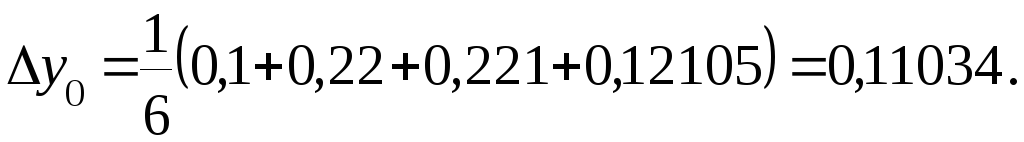
11) Получаем

Значения заносим в строку, помеченную индексом , и снова проводим вычисления по формулам (3).

0	0	1	0,1	0,1
	0,05	1,05	0,11	0,22
	0,05	1,055	0,1105	0,221	0,05
	0,1	1,1105	0,12105	0,12105
1	0,1	1,11034	0,12103	0,12103
	0,15	1,17085	0,13208	0,26417
	0,15	1,17638	0,113264	0,26528	0,051
	0,2	1,24298	0,12429	0,12429
2	0,2	1,2428	0,14428	0,14428
	0,25	1,31494	0,15649	0,31298
	0,25	1,32105	0,15710	0,31421	0,049
	0,3	1,3999	0,16999	0,16999
3	0,3	1,39971	0,16997	0,16997
	0,35	1,48469	0,18347	0,36694
	0,35	1,49144	0,18414	0,36829	0,049
	0,4	1,58384	0,19838	0,19838
4	0,4	1,58364	0,19836	0,19836
	0,45	1,68282	0,21328	0,42656
	0,45	1,69028	0,21403	0,42806	0,05
	0,5	1,79767	0,29977	0,22977
5	0,5	1,79743

Из шестого столбца таблицы видно, что шаг выбран правильно.

Таблица сравнения методов Эйлера, Рунге-Кутта и точного решения уравнения.

x	Метод Эйлера	Метод Рунге-Кутта	Точное решение
	y	y	y
0	1	1	1
0,1	1,1	1,11034	1,11034
0,2	1,22	1,2428	1,2428
0,3	1,362	1,39971	1,3997
0,4	1,528	1,58364	1,58365
0,5	1,721	1,79743	1,79744

17