
- •Федеральное агентство по образованию
- •1. Основные понятия и задачи
- •1.1. Основные задачи теории корреляции
- •1.2. Задачи регрессионного анализа
- •1.3. Корреляционная таблица
- •1.4. Выборочное уравнение прямой линии регрессии по сгруппированным данным. Выборочный коэффициент корреляции
- •1.5. Свойства выборочного коэффициента корреляции
- •1.6. Точечная и интервальная оценки коэффициентов корреляции нормально распределенной генеральной совокупности
- •1.7. Проверка гипотезы о значимости выборочного коэффициента корреляции
- •1.8. Корреляционное отношение
- •1.9. Свойства корреляционного отношения
- •1.10. Проверка однородности нескольких дисперсий, найденных по выборкам одинаковых объемов
- •1.11. Проверка однородности нескольких дисперсий, найденных по выборкам различного объема
- •1.12. Проверка адекватности регрессионной модели
- •1.13. Порядок проверки адекватности модели
- •1.14. Коэффициент детерминации
- •2. Пример выполнения расчетно-графической работы
- •2.1. Определение основных параметров случайных величин и
- •2.2. Построение корреляционной таблицы
- •2.3. Проверка однородности дисперсий случайных величин ипо критерию Бартлетта
- •2.4. Построение линейной регрессионной модели
- •2.9. Нахождение средней квадратической ошибки уравнения
- •2.10. Интервальные оценки параметров квадратичной линии регрессии генеральной совокупности
- •2.11. Нахождение коэффициента детерминации
- •2.12. Проверка адекватности регрессионной модели
- •Список литературы:
1.8. Корреляционное отношение
Ранее рассматривалась теснота линейной корреляционной связи. Вопрос: как оценить тесноту любой корреляционной связи?
Так как все значения
признака
![]() разбиты на группы, можно представить
общую дисперсию признака в виде суммы
внутригрупповой и межгрупповой дисперсии.
разбиты на группы, можно представить
общую дисперсию признака в виде суммы
внутригрупповой и межгрупповой дисперсии.
![]() .
(9)
.
(9)
Определение. Групповой дисперсией называют дисперсию значений признака, принадлежащих группе, относительно групповой средней.
![]() ,
(10)
,
(10)
где
![]() – частота значений
– частота значений![]() при
при![]() ,
,
![]() – номер группы,
– номер группы,
![]() ,
,
![]() –групповая
средняя группы
–групповая
средняя группы
![]() ,
,
![]() – объем группы
– объем группы
![]() .
.
Определение. Внутригрупповой дисперсией называют среднюю арифметическую групповых дисперсий, взвешенную по объемам групп.
![]() ,
(11)
,
(11)
![]() –объем всей
совокупности.
–объем всей
совокупности.
Определение. Межгрупповой дисперсией называют дисперсию групповых средних относительно общeй средней.
![]() ,
(12)
,
(12)
где
![]() – общая средняя.
– общая средняя.
Определение. Общей дисперсией называют дисперсию значений признака всей совокупности относительно общей признака.
![]() .
(13)
.
(13)
Для оценки тесноты нелинейной корреляционной связи вводят корреляционные характеристики:
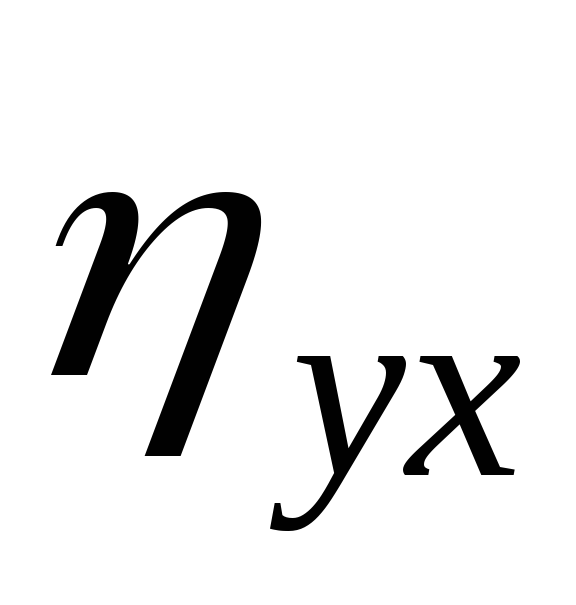 –выборочное
корреляционное отношение
–выборочное
корреляционное отношение
 к
к
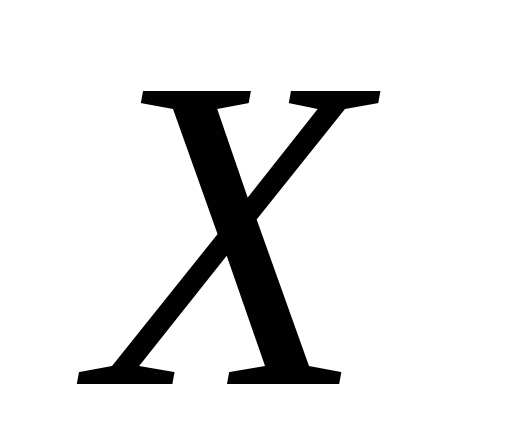 .
.
![]() (14)
(14)
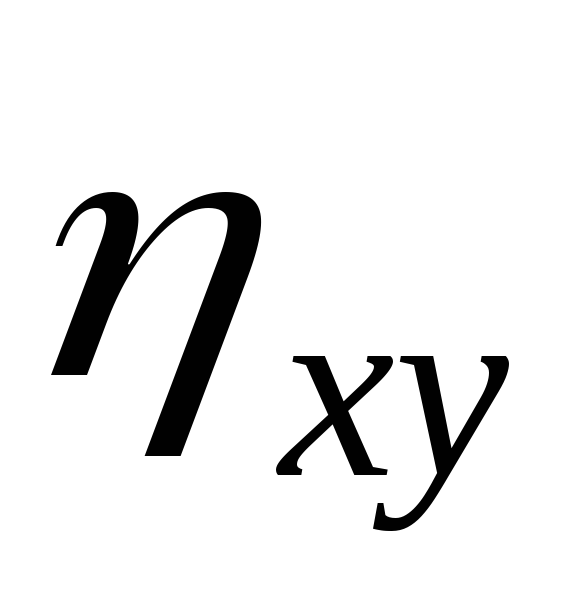 –выборочное
корреляционное отношение
–выборочное
корреляционное отношение
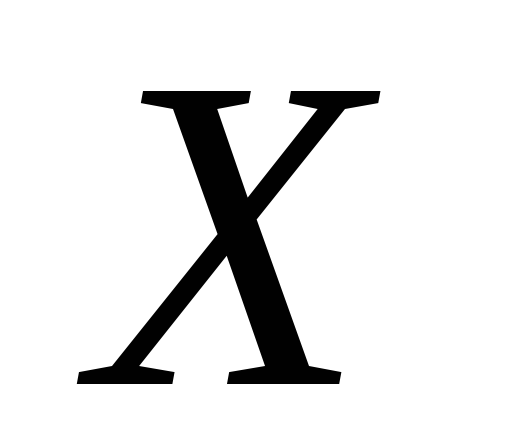 к
к
 .
.
![]() (15)
(15)
1.9. Свойства корреляционного отношения
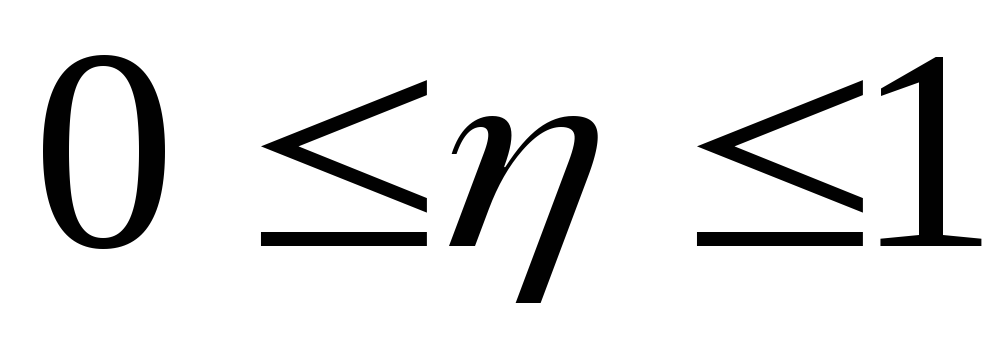 .
.Если
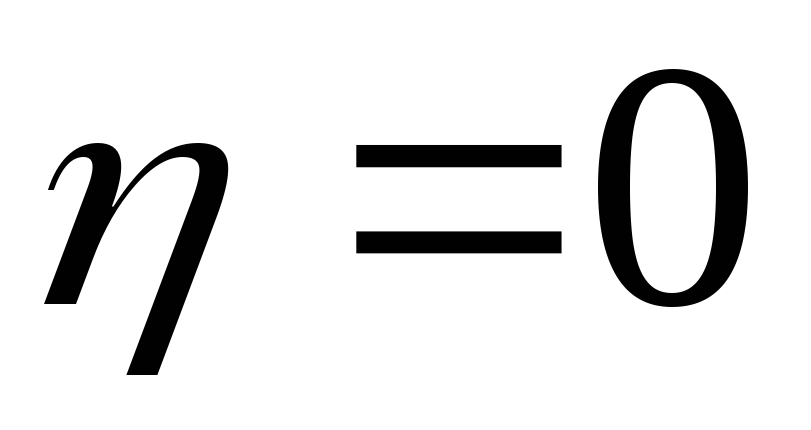 ,
то признак
,
то признак
 с признаком
с признаком
 корреляционной зависимостью не связан.
корреляционной зависимостью не связан.
Если
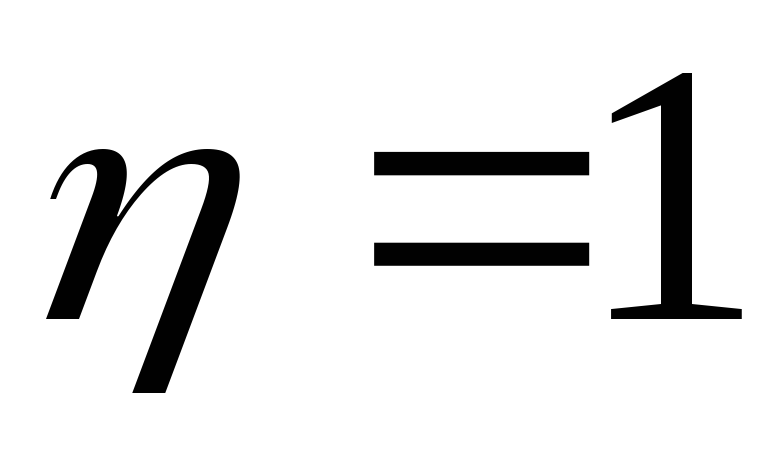 ,
то признак
,
то признак
 с признаком
с признаком
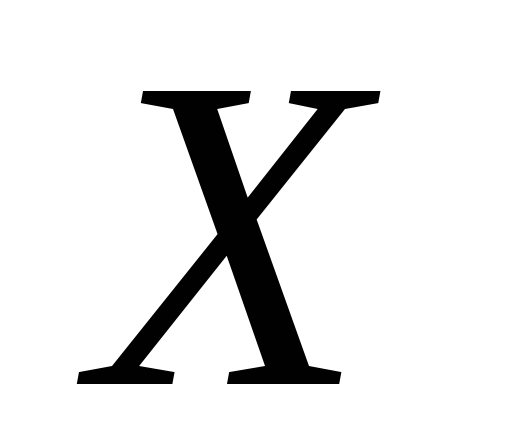 связан функциональной зависимостью.
связан функциональной зависимостью.Выборочное корреляционное отношение не менее абсолютной величины выборочного коэффициента корреляции:
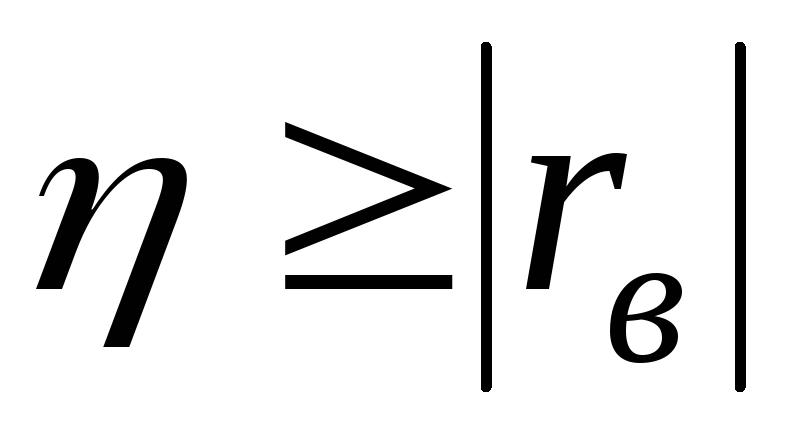 .
.Если выборочное корреляционное отношение равно абсолютной величине выборочного коэффициента корреляции, то имеет место точная линейная корреляционная зависимость.
1.10. Проверка однородности нескольких дисперсий, найденных по выборкам одинаковых объемов
Для проверки
гипотезы
![]() об однородности нескольких дисперсий
при равных объемах всех рассматриваемых
выборок,
об однородности нескольких дисперсий
при равных объемах всех рассматриваемых
выборок,![]() может быть использован
может быть использован![]() – критерий Кочрена.
– критерий Кочрена.
Пусть
![]() – количество выборочных дисперсий,
однородность которых проверяется.
Обозначим эти дисперсии
– количество выборочных дисперсий,
однородность которых проверяется.
Обозначим эти дисперсии![]() .
.
Вычисляется
расчетное
![]() – отклонение по формуле:
– отклонение по формуле:
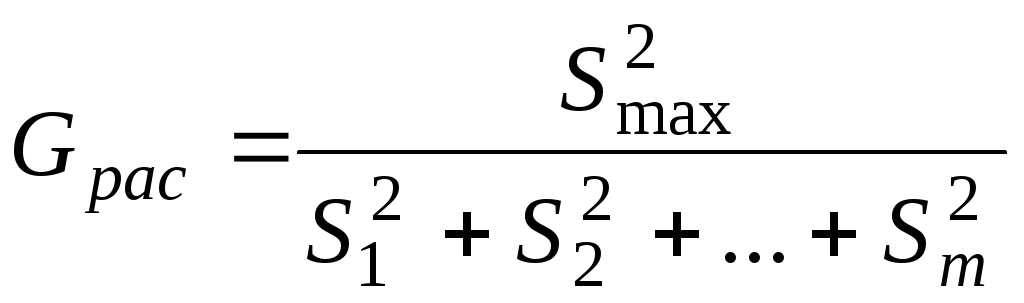 .
(16)
.
(16)
В числителе этой формулы стоит наибольшая из рассматриваемых дисперсий, а в знаменателе – сумма всех дисперсий. Далее обращаются к таблицам распределения Кочрена.
По выбранному
уровню значимостью
![]() ,
числу степеней свободы каждой выборки
,
числу степеней свободы каждой выборки![]() и по количеству выборок
и по количеству выборок![]() ,
из этой таблицы отыскиваем величину
,
из этой таблицы отыскиваем величину![]() .
Если
.
Если![]() ,
то можно принять гипотезу об однородности
дисперсии, в противном случае гипотеза
отвергается.
,
то можно принять гипотезу об однородности
дисперсии, в противном случае гипотеза
отвергается.
1.11. Проверка однородности нескольких дисперсий, найденных по выборкам различного объема
Пусть проверяется
однородность некоторого числа
![]() дисперсий
дисперсий![]() .
Но эти дисперсии найдены по выборкам
различного объема
.
Но эти дисперсии найдены по выборкам
различного объема![]() .
В этом случае используется критерий
Бартлетта.
.
В этом случае используется критерий
Бартлетта.
Предварительно
вычисляют дисперсию воспроизводимости
![]() ,
представляющую собой среднее взвешенное
значение дисперсий, взятое с учетом
числа степеней свободы:
,
представляющую собой среднее взвешенное
значение дисперсий, взятое с учетом
числа степеней свободы:
![]() ,
(17)
,
(17)
где
![]() – число степеней свободы соответствующих
дисперсий,
– число степеней свободы соответствующих
дисперсий,
![]() – сумма всех степеней свободы:
– сумма всех степеней свободы:
![]() .
.
Рассчитываем величину
![]() ,
,
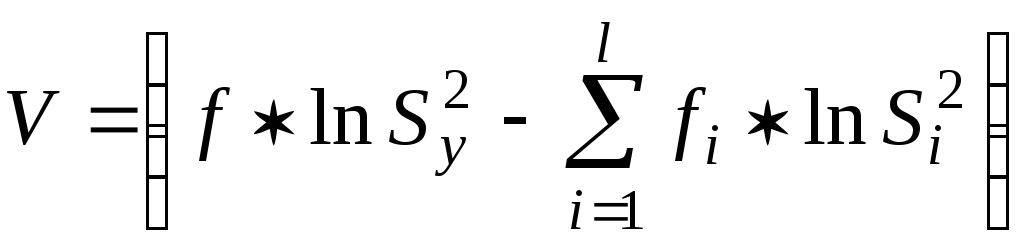 ,
,
 .
(18)
.
(18)
Затем по таблице
«Критерий
![]() »
при уровне значимости
»
при уровне значимости
![]() и числе степеней свободы
и числе степеней свободы![]() ,
отыскивают значение
,
отыскивают значение![]() .
.
Гипотеза об
однородности дисперсий принимается,
если
![]() .
.
Замечание. В данной проверке требуется, чтобы объем каждой выборки был не менее четырех.
Замечание. Критерий Бартлетта чувствителен к отклонениям от нормального распределения.
