
3.2 Синтез ких-фильтров методом окон. Постановка задачи
Методы, основанные на использовании окон, полезны, в частности, при разработке фильтров, задаваемых с помощью эталонных простых частотных характеристик, таких, например, как идеальный низкочастотный, полосовой, режекторный и высокочастотный фильтры. Примеры этих четырех фильтров показаны на рисунке 3.1.
|
а) Идеальный ФНЧ |
б) Идеальный ФВЧ | |||||||||||||||
|
|
| |||||||||||||||
|
в) Идеальный ПФ |
г) Идеальный РФ | |||||||||||||||
|
|
| |||||||||||||||
|
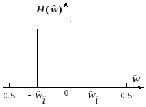
Рисунок 3.1 – Частотные характеристики идеальных фильтров Без потери общности зададимся целью рассчитать коэффициенты (импульсную характеристику) фильтра НЧ (рисунок 3.1,а). Рассматриваемый фильтр имеет идеальную АЧХ, периодически повторяющуюся с частотой дискретизации, а потому его частотная характеристика может быть представлена бесконечным рядом Фурье:
Если
Допустив,
что характеристика
Импульсные
характеристики идеальных фильтров
верхних частот, полосовых и режекторных
приведены в таблице 3.1. Импульсная
характеристика фильтра НЧ изображена
на рисунке 3.2, из которого видно, что
Таблица 3.1 – Идеальная импульсная характеристика стандартных частотно-избирательных фильтров
Рисунок 3.2 – Импульсная характеристика идеального фильтра нижних частот
Описанный
простой подход связан с некоторыми
проблемами. Важнейшая из них следующая:
хотя характеристика
Простейший
путь конструирования физически
возможной передаточной функции состоит
в исключении всех членов ряда (2.3),
имеющих отрицательный индекс
3.2.1 ПРЯМОУГОЛЬНОЕ ОКНО
Наиболее
простой и непосредственный способ
усечения идеальной импульсной
характеристики
как показано на рисунке 3.3:
Рисунок 3.3 – Прямоугольное окно
Результирующая
импульсная характеристика
Рисунок 3.4 Импульсная характеристика а) результат обработки прямоугольным окном б) после переиндексации ПРИМЕР 3.1
Найти
импульсную характеристику после
обработки прямоугольным окном для
идеального ФНЧ с частотой среза
Положим
РЕШЕНИЕ:
Для
Импульсная характеристика фильтра после обработки прямоугольным окном и переиндексации показана на рисунке 3.5.
Рисунок 3.5,а – Импульсная характеристика фильтра для примера 3.1 Результат процедуры усечения с использованием (3.4) позволяет получить частотную характеристику фильтра (рисунок 3.5,б)
и
передаточную функцию
Казалось
бы, решение найдено. Действительно,
подбирая значения
В
результате формируются пульсации АЧХ
как в полосе задерживания, так и в
полосе пропускания; кроме того
образуется переходная полоса
Рисунок 3.5,б – Амплитудно-частотная характеристика фильтра для примера 3.1
а)
Импульсная характеристика,
б)
Амплитудно-частотная характеристика,
Рисунок
3.6 – Импульсная и амплитудная
характеристики идеального усеченного
фильтра с линейной фазовой характеристикой
при
Можно
показать, что причиной появления
всплесков и провалов в характеристике
КИХ-фильтра является частотная
характеристика прямоугольного окна
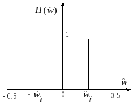
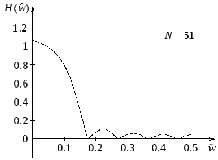
Рисунок 3.7 – Частотная характеристика прямоугольного окна
Это
быстроколеблющаяся функция, резко
спадающая по амплитуде. Область с
максимальной амплитудой называется
главным лепестком, а остальные области
– боковыми лепестками. Ширина всех
лепестков, включая главный, одинакова
и равна
Таким образом, прямоугольное окно позволяет сделать вывод о том, что «хорошее» окно должно обладать двумя свойствами: 1. Ширина главного лепестка частотной характеристики должна быть малой;
2.
Энергия боковых лепестков частотной
характеристики должна быстро уменьшаться
с увеличением частоты
Ясно что, эти два требования несовместимы и необходим компромиссный вариант.
Если
мы хотим разработать фильтры с лучшей
аппроксимацией в области перехода,
то необходимо использовать окно
Был предложен ряд различных окон. Рассмотрим некоторые из них для того, чтобы показать эффект применения окон и их относительные достоинства. 3.2.2 ОКНО БЛЭКМАНА
Окно
Блэкмана при использовании для
разработки КИХ-фильтров позволяет
получить еще меньшее значение колебаний
АЧХ в области подавления (уменьшаются
до
Аналитически оно задаётся выражением:
Однако,
ширина главного лепестка в
амплитудно-частотной характеристике
окна Блэкмана примерно на
3.2.3 МЕТОДИКА СИНТЕЗА КИХ-ФИЛЬТРОВ МЕТОДОМ ОКОН
Напомним,
что отсчеты импульсной характеристики
Методика синтеза включает в себя:
1.
Задание требований к фильтру. Для
этого следует задать «идеальную» или
желаемую частотную характеристику
фильтра
2.
Получить импульсную характеристику
Конечно
же, определение импульсной характеристики
зависит от длины
3.
Выбрать весовую функцию, которая
удовлетворяет требованиям к полосе
пропускания или затуханию, а затем
определить число коэффициентов фильтра
4. Расчет импульсной характеристики реального фильтра.
Расчет
осуществляется по формуле
Поскольку
импульсная характеристика найдена,
то, казалось бы, процедура на этом
должна быть завершена. К сожалению,
вследствие приближенной оценки
параметра
5. Проверка выполнения заданных требований.
Для
проверки выполнения заданных требований
рассчитывается АЧХ: если требования
задания к АЧХ выполняются, то на этом
процедуру конструирования передаточной
функции можно завершить; если требования
не удовлетворяются, то необходимо
увеличить порядок
Может
случиться так, что требования выполняются
с большим запасом, тогда следует
проверить, нельзя ли уменьшить
Может случиться и так, что при выбранном окне длина фильтра оказывается слишком большой, а фильтр такой длины по каким-либо соображениям (большие собственные шумы, обеспечение работы в реальном масштабе времени, элементная база и т.п.) не может быть реализован. Тогда выбирается другое окно и процедура повторяется.
3.2.4 ПЛЮСЫ И МИНУСЫ МЕТОДА ОКОН Важным достоинством метода взвешивания является простота: его просто применять и легко понять. Этот метод включает минимальный объем вычислений даже при использовании сложной функции Кайзера. Главный недостаток метода – отсутствие гибкости. Максимальная неравномерность в ПП и ПЗ примерно равны, так что разработчик может получить фильтр либо со слишком маленькой неравномерностью ослабления в ПП, либо со слишком большим затуханием в ПЗ.
Вследствие
того, что в методе фигурирует свертка
спектра вырезающей функции
Для
функции окон (исключая функцию Кайзера)
максимальная
амплитуда
колебаний в частотной характеристике
фиксирована и не зависит от того,
насколько большим делать
В
некоторых случаях выражения формулы
желаемой АЧХ
| ||||||||||||||||



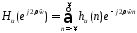 ; (3.1)
; (3.1) известна, то
известна, то можно получить, применив обратное
преобразование Фурье к
можно получить, применив обратное
преобразование Фурье к
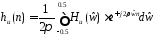 ; (3.2)
; (3.2)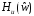 не равна нулю от
не равна нулю от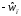 до
до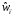 ,
упрощаем интегрирование и получаем
следующую импульсную
характеристику:
,
упрощаем интегрирование и получаем
следующую импульсную
характеристику: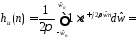
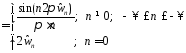 (3.3)
(3.3)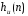 симметрична относительно
симметрична относительно ,
т.е.
,
т.е.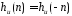 ,
так что фильтр будет иметь линейную
(в данном случае нулевую) фазовую
характеристику.
,
так что фильтр будет иметь линейную
(в данном случае нулевую) фазовую
характеристику. ,
,
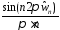

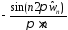
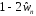
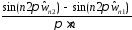
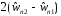
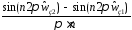
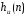 уменьшается при удалении от точки
уменьшается при удалении от точки ,
она длится теоретически до
,
она длится теоретически до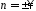 .
Следовательно, полученный фильтр не
является КИХ-фильтром. Кроме того,
такой фильтр физически нереализуем,
т.к.
.
Следовательно, полученный фильтр не
является КИХ-фильтром. Кроме того,
такой фильтр физически нереализуем,
т.к.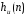 имеет отсчеты при
имеет отсчеты при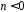 ,
т.е. в нем реакция предшествует
воздействию.
,
т.е. в нем реакция предшествует
воздействию.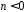 и ограничения (усечения) импульсной
характеристики сверху до
и ограничения (усечения) импульсной
характеристики сверху до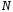 членов.
членов.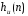 – это оставить неизмененными её
значения в пределах некоторого
интервала, скажем, от
– это оставить неизмененными её
значения в пределах некоторого
интервала, скажем, от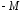 до
до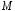 .
Это эквивалентно умножению
.
Это эквивалентно умножению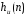 на прямоугольную функцию, задаваемую
выражением:
на прямоугольную функцию, задаваемую
выражением: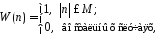 (3.4)
(3.4)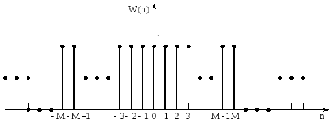
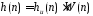 имеет длину
имеет длину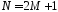 .
Импульсная характеристика после
обработки окном (рисунок 3.4,а) будет
физически нереализуемой, т.е. такой,
что имеет ненулевые значения при
.
Импульсная характеристика после
обработки окном (рисунок 3.4,а) будет
физически нереализуемой, т.е. такой,
что имеет ненулевые значения при .
Для того, чтобы сделать её физически
реализуемой, необходимо сдвинуть
начало отсчета времени до первого
нулевого индекса и переиндексировать
составляющие. Этот процесс проиллюстрирован
на рисунке 3.4
.
Для того, чтобы сделать её физически
реализуемой, необходимо сдвинуть
начало отсчета времени до первого
нулевого индекса и переиндексировать
составляющие. Этот процесс проиллюстрирован
на рисунке 3.4
 .
.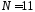 .
.
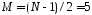
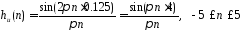
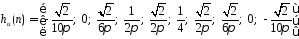

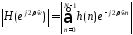 (3.5,а)
(3.5,а) .
(3.5,б)
.
(3.5,б)  и контролируя поведение АЧХ, за
несколько интерраций можно найти
такое
и контролируя поведение АЧХ, за
несколько интерраций можно найти
такое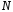 ,
при котором требования к заданному
фильтру будут выполнены. Однако,
усечение ряда Фурье приводит к
существенным ошибкам, которые выражаются
в появлении пульсаций вблизи частоты
среза. Максимум этих пульсаций слева
и справа составляет
,
при котором требования к заданному
фильтру будут выполнены. Однако,
усечение ряда Фурье приводит к
существенным ошибкам, которые выражаются
в появлении пульсаций вблизи частоты
среза. Максимум этих пульсаций слева
и справа составляет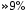 от АЧХ и остается таковым вне зависимости
от величины
от АЧХ и остается таковым вне зависимости
от величины .
Этот феномен получил название Явление
Гиббса.
.
Этот феномен получил название Явление
Гиббса.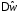 ,
ширина которой тем меньше, чем больше
значения
,
ширина которой тем меньше, чем больше
значения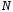 .
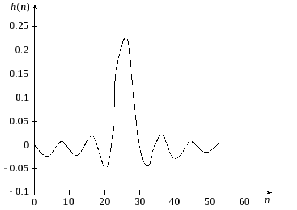
Рисунок 2.6 показывает импульсную
.
Рисунок 2.6 показывает импульсную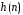 и частотную характеристики
и частотную характеристики ,
полученные при использовании
прямоугольного окна для
,
полученные при использовании
прямоугольного окна для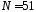 .
.

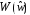 .
График этой функции будет иметь форму,
показанную на рисунке 3.7.
.
График этой функции будет иметь форму,
показанную на рисунке 3.7.
 ,
причем с увеличением
,
причем с увеличением ширина главного лепестка уменьшается
и увеличивается число пульсаций. Так
как ширина главного лепестка определяет
ширину полосы перехода синтезируемого
фильтра, то ясно, что чем больше
ширина главного лепестка уменьшается
и увеличивается число пульсаций. Так
как ширина главного лепестка определяет
ширину полосы перехода синтезируемого
фильтра, то ясно, что чем больше ,
тем уже переходная полоса, тем меньше
амплитуда пульсаций в области полос
пропускания и задерживания при
неизменной величине амплитуды пульсаций
,
тем уже переходная полоса, тем меньше
амплитуда пульсаций в области полос
пропускания и задерживания при
неизменной величине амплитуды пульсаций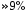 вблизи частоты среза.
вблизи частоты среза.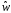 .
. с более плавной амплитудной
характеристикой, чем у прямоугольного
окна. В этом случае идеальная импульсная
характеристика
с более плавной амплитудной
характеристикой, чем у прямоугольного
окна. В этом случае идеальная импульсная
характеристика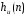 перемножается с функцией окна
перемножается с функцией окна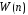 ,
имеющей конечный размер
,
имеющей конечный размер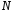 ,
в результате чего получается конечная
импульсная характеристика реального
фильтра
,
в результате чего получается конечная
импульсная характеристика реального
фильтра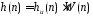 .
. )
по сравнению с окном Хэмминга.
)
по сравнению с окном Хэмминга.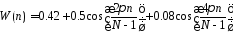 , (3.9)
, (3.9) .
. шире, чем для окна Хэмминга и в три
раза шире, чем для прямоугольного
окна.
шире, чем для окна Хэмминга и в три
раза шире, чем для прямоугольного
окна.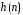 КИХ-фильтров одновременно являются
и коэффициентами
КИХ-фильтров одновременно являются
и коэффициентами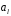 его передаточной функции
его передаточной функции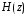 ,
поэтому задача синтеза сводится к
получению импульсной
характеристики.
,
поэтому задача синтеза сводится к
получению импульсной
характеристики.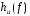
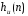 желаемого фильтра, найдя для этого
Фурье–образ частотной характеристики
(формулы 3.2, 3.3). Выражения
желаемого фильтра, найдя для этого
Фурье–образ частотной характеристики
(формулы 3.2, 3.3). Выражения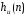 для стандартных частотно-избирательных
фильтров приведены в таблице 3.1. При
этом следует учесть эффект смазывания
характеристики, вводимого весовой
функцией, из-за которого частота среза
получающегося фильтра будет отличаться
от представленной в спецификации. Для
этого во всех расчетных выражениях
для
для стандартных частотно-избирательных
фильтров приведены в таблице 3.1. При
этом следует учесть эффект смазывания
характеристики, вводимого весовой
функцией, из-за которого частота среза
получающегося фильтра будет отличаться
от представленной в спецификации. Для
этого во всех расчетных выражениях
для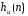 и
и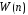 следует в качестве частоты среза
использовать не
следует в качестве частоты среза
использовать не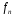 ,
а центр полосы перехода, то есть
,
а центр полосы перехода, то есть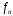 заменяют на
заменяют на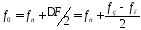 .
.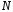 ;
в свою очередь, выбор
;
в свою очередь, выбор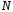 связан с типом используемого окна.
связан с типом используемого окна.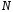 ,
использовав подходящее выражение для
связи длины фильтра с шириной перехода
,
использовав подходящее выражение для
связи длины фильтра с шириной перехода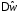 .
В случае выбора окна Кайзера длина
.
В случае выбора окна Кайзера длина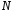 определяется по формуле.
определяется по формуле.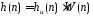 ,
где расчетное выражение
,
где расчетное выражение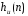 берется из таблицы 3.1 с подстановкой
величины
берется из таблицы 3.1 с подстановкой
величины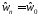 .
.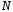 ,
от которого полностью зависит
импульсная
характеристика, а потому и частотные
свойства фильтра, полученный фильтр
крайне редко удовлетворяет заданным
требованиям, что вызывает необходимость
проверить
их выполнение.
,
от которого полностью зависит
импульсная
характеристика, а потому и частотные
свойства фильтра, полученный фильтр
крайне редко удовлетворяет заданным
требованиям, что вызывает необходимость
проверить
их выполнение. и повторить п.п.2–5.
и повторить п.п.2–5.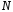 .
Иначе говоря, за некоторое количество
итераций (проб) обязательно найдется
наименьшее значение
.
Иначе говоря, за некоторое количество
итераций (проб) обязательно найдется
наименьшее значение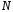 ,
при котором требования выполняются.
,
при котором требования выполняются.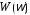 и желаемой характеристики АЧХ
и желаемой характеристики АЧХ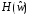 , невозможно
точно задать граничные частоты ПП и
ПЗ.
, невозможно
точно задать граничные частоты ПП и
ПЗ.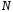 (от величины
(от величины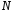 зависит только ширина полосы перехода).
Следовательно, затухание в полосе
подавления фиксировано для данной
функции. Таким образом, для данной
спецификации затухания разработчик
должен выбрать подходящую функцию.
зависит только ширина полосы перехода).
Следовательно, затухание в полосе
подавления фиксировано для данной
функции. Таким образом, для данной
спецификации затухания разработчик
должен выбрать подходящую функцию.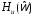 будут настолько сложными, что из
уравнения (3.2) аналитически находить
будут настолько сложными, что из
уравнения (3.2) аналитически находить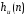 нет смысла. В таких случаях
нет смысла. В таких случаях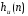 можно получить с помощью метода
частотной выборки, а уже затем применять
весовую функцию.
можно получить с помощью метода
частотной выборки, а уже затем применять
весовую функцию.