Основные понятия теории нечетких множеств |
1 |
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ И ЛИНГВИСТИЧЕСКИХ ПЕРЕМЕННЫХ
1. Понятие и основные характеристики нечеткого множества
Определение 1.1. Пусть X – универсальное множество. Нечетким множеством A на множестве X (нечетким подмножеством A множества X) называется совокупность пар
A = {< μA(x), x >}, (1.1)
где x X, μA(x) [0, 1]. X называется областью определения нечеткого множества A, а μA – функцией принадлежности этого множества. Значение функции принадлежности μA(x) для конкретного элемента x X называется степенью принадлежности этого элемента нечеткому множеству A.
Интерпретацией функции принадлежности является субъективная мера того, насколько элемент x X соответствует понятию, смысл которого формализуется нечетким множеством A. При этом значение, равное 1, означает полное (абсолютное) соответствие, значение, равное 0 – полное (абсолютное) несоответствие.
Определение 1.2. Нечеткие множества с дискретной областью определения называют дискретными нечеткими множествами, не-
четкие множества с непрерывной областью определения – непрерыв-
ными нечеткими множествами.
Обычные (четкие) множества можно также рассматривать в нечетком контексте. Функция принадлежности обычного множества может принимать только два значения: 0, если элемент не принадлежит множеству, и 1, если элемент ему принадлежит.
В литературе можно встретить различные формы записи нечетких множеств. Для дискретной области определения X={x1, x2, …, xn} (возможен также случай n = ∞) существуют следующие формы:
A = {<x1, μA(x1)>, <x2, μA(x2)>, …, <xn, μA(xn)>}; |
(1.2) |
A = {μA(x1)/x1, μA(x2)/x2, …, μA(xn)/xn}; |
(1.3) |
n |
|
A = μA(x1)/x1+μA(x2)/x2+…+μA(xn)/xn = ∑μA (xj ) / xj . |
(1.4) |
j =1
Основные понятия теории нечетких множеств |
2 |
Символы «+» и «Σ» имеют в данном случае смысл поточечного объединения, а не суммирования. Для непрерывного случая возможны
формы записи: |
|
A = < X; μA >; |
(1.5) |
A=∫μA (x) / x , |
(1.6) |
X
где знак интеграла имеет смысл поточечного объединения на X. Кроме того, как для дискретного, так и для непрерывного случаев применяется обобщенная форма записи:
A= μA (x) / x . |
(1.7) |
X |
|
Примерами непрерывных нечетких |
множеств могут являться |
B ={x x ≈ 2} – множество вещественных чисел, приблизительно равных 2, и C ={x x >>1} – множество вещественных чисел, на-
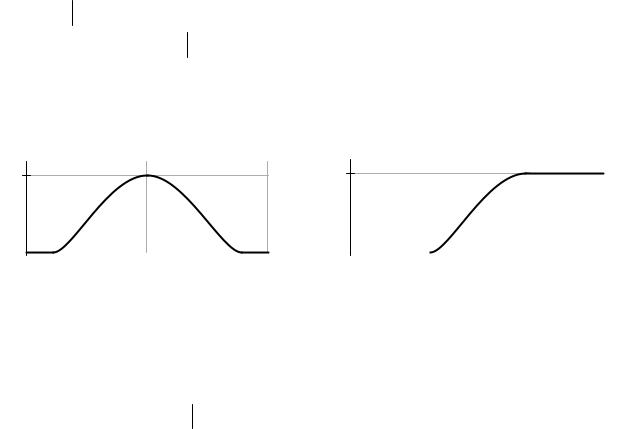
много бóльших 1. Возможные формы функций принадлежности этих множеств схематически представлены на рис. 1.1 и рис. 1.2 соответственно.
С
1
|
|
|
|
|
|
|
0 |
|
|
|
x |
|
|
|
|
|
|
|
1 |
||||
Рис. 1.1. Функция принадлежности |
Рис. 1.2. Функция принадлежности |
||||||||||
нечеткого множества чисел, |
|
нечеткого множества чисел, |
|
||||||||
|
|
приблизительно равных 2 |
|
|
|
намного бóльших 1 |
|
||||
В качестве примера дискретного нечеткого множества можно рассмотреть D ={n n ≈1} – множество целых чисел, близких к 1,
возможная форма задания которого следующая:
N = {0.2/-3; 0.4/-2; 0.6/-1; 0.8/0; 1/1; 0.8/2; 0.6/3; 0.4/4; 0.2/5} (остальные точки имеют нулевую степень принадлежности).
Конкретный вид функции принадлежности зависит от смысла, вкладываемого в формализуемое понятие в условиях конкретной задачи, и часто имеет субъективную природу. Большинство методов построения функций принадлежности в той или иной мере основано на обработке информации, получаемой экспертным путем.
Основные понятия теории нечетких множеств |
3 |
Пусть A – нечеткое множество на множестве X. Введем еще несколько определений.
Определение 1.3. Нечеткое множество называется пустым, если его функция принадлежности тождественно равна нулю на всей области определения.
Определение 1.4. Высотой нечеткого множества называется величина
hA = sup μA (x). |
(1.8) |
x X |
|
Примечание 1. Здесь sup (супремум) – точная верхняя грань функции принадлежности. Если множество X (область определения) является замкнутым, то супремум функции совпадает с ее максимумом.
Определение 1.5. Если hA = 1, то нечеткое множество A называ-
ется нормальным, иначе (hA < 1) – субнормальным.
Определение 1.6. Носителем нечеткого множества A называется множество
Supp A = {x X μA(x) > 0}. |
(1.9) |
Таким образом, носитель нечеткого множества |
содержит все |
элементы области определения, хоть в какой-то степени соответствующие формализуемому понятию.
Примечание 2. Не следует путать обозначения sup и Supp. Первое является сокращением от supremum, второе – от support.
Определение 1.7. Множеством уровня α (α-срезом) нечеткого
множества A (0 < α ≤ 1) называется множество |
|
Aα={x X μA(x) ≥ α}. |
(1.10) |
Можно показать, что для однозначного задания нечеткого множества достаточно указать все его множества уровня. Таким образом, имеется два способа задания нечеткого множества – на основе функции принадлежности и на основе множеств уровня.
Определение 1.8. Множества уровня 1 (1-срез) называется
ядром нечеткого множества A: |
|
Core A = {x X μA(x) = 1}. |
(1.11) |
Ядро нечеткого множества, тем самым, содержит все элементы области определения, полностью соответствующие формализуемому понятию.
Основные понятия теории нечетких множеств |
4 |
Очевидно, что множества уровня обладают свойством монотон-
ности относительно вложения, т.е.
(α ≥ β) (Aα Aβ ) , |
(1.12) |
откуда следует, что элемент, принадлежащий множеству уровня α, принадлежит также всем множествам меньших уровней β ≤ α.
Определение 1.9. Пусть A и B – нечеткие множества на множестве X с функциями принадлежности μA и μB соответственно. Гово-
рят, что A является нечетким подмножеством B (B включает в себя
A), если выполнено следующее условие:
x X μA (x)≤ μB (x) . |
(1.13) |
В качестве примера включения нечетких множеств можно привести нечеткое множество чисел, близких к 1, включающее в себя нечеткое множество чисел, очень близких к 1 (модификатор «очень» в данном случае рассматривается как усиливающий требование выполнения свойства «быть близким»).
Определение 1.10. Нечеткие множества A и B на множестве X
равны (совпадают), если:
x X μA (x) = μB (x) . |
(1.14) |
Среди нечетких множеств с числовой областью определения выделяют также класс нечетких чисел и нечетких интервалов. Для определения этого класса вводится понятие выпуклости нечетких множеств.
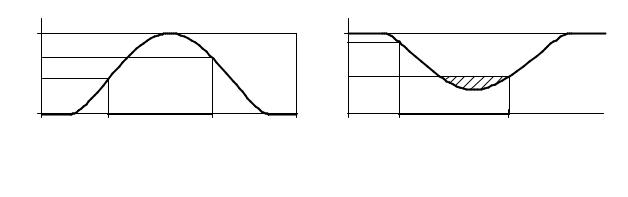
Определение 1.11. Нечеткое подмножество A вещественной оси называется выпуклым, если выполняется следующее условие:
x1, x2 |
X , λ [0, 1] |
(1.15) |
|
μA (λx1 +(1−λ)x2 ) ≥min{μA (x1 ), μA (x2 )}. |
|||
|
|||
На рис. 1.3 показаны примеры выпуклого (слева) и невыпуклого (справа) нечетких множеств.
Рис. 1.3. К определению выпуклости нечеткого множества
Основные понятия теории нечетких множеств |
5 |
Определение 1.12. Нечетким интервалом называется выпуклое нормальное нечеткое множество на числовой области определения, имеющее непрерывную функцию принадлежности и непустое ядро. Нечетким числом называется нечеткий интервал, ядро которого содержит в точности один элемент.
Для нечетких интервалов и чисел существует теорема представления, согласно которой нечеткое подмножество A вещественной оси является нечетким интервалом тогда и только тогда, когда его функция принадлежности представима в виде:
|
LA (x), a0 ≤ x <a1, |
|
|||||
|
|
|
|
|
|
|
|
μA |
1, a 1 ≤ x≤b 1 |
|
|
(1.16) |
|||
(x) = |
R |
|
(x), b < u ≤b |
|
, |
||
|
|
A |
0 |
|
|||
|
|
1 |
|
|
|||
|
|
|
|
иначе. |
|
|
|
|
0, |
|
|
|
|||
Функции LA и RA называются соответственно левой и правой ветвью функции принадлежности нечеткого числа. Эти функции непрерывны, при этом LA на отрезке [a0, a1] возрастает от LA(a0) = 0 до
LA(a1) = 1, а RA на отрезке [b1, b0] убывает от RA(b1) = 1 до RA(b0) = 0 (рис. 1.4).
Рис. 1.4. К определению нечеткого интервала 
Определение 1.13. Пусть A ={A1, A2 ,…, An} – семейство нечетких множеств, заданных на области определения X. Ã называется нечетким разбиением X с параметром α (0 < α ≤ 1), если все множества Aj являются выпуклыми и нормальными, и выполняется условие:
x X j {1,…, n} μAj (x) ≥α |
(1.17) |
(т.е. любой элемент области определения принадлежит хотя бы одному из множеств семейства Ã со степенью, не меньшей α – рис. 1.5).