2. Примеры решения задач

1. Вычислить .

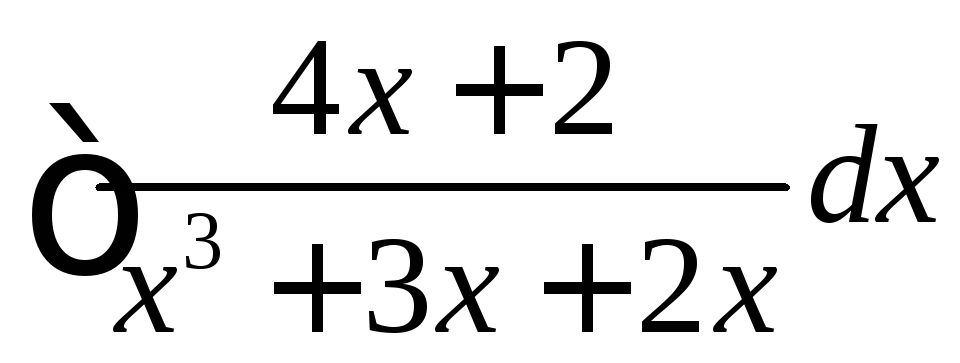◄ Рассматриваемая дробь правильная, так как степень числителя меньше степени знаменателя.

Знаменатель дроби разложим на множители. Сначала вынесем общий множитель x: . Для разложения на множители квадратного трехчленанадо найти его корни:

, ,.

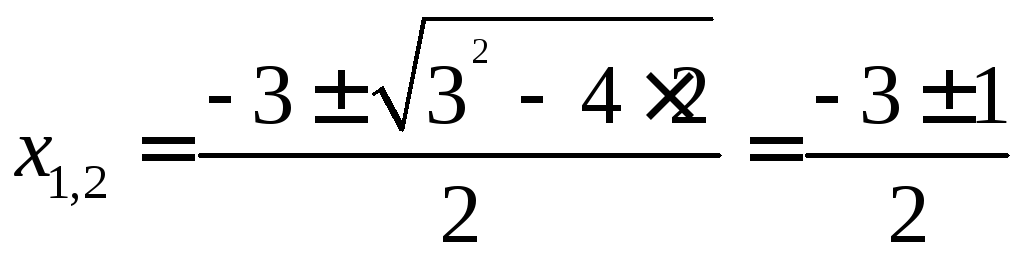Поэтому , а

.

Теперь ищем разложение дроби на сумму простейших в виде

,

где числа A, B и C подлежат определению. Множителю x в знаменателе соответствует простейшая дробь , множителю– дробь , множителю – дробь .

Для нахождения A, B и C приведём правую часть к общему знаменателю (он тот же, что и в левой части)

.

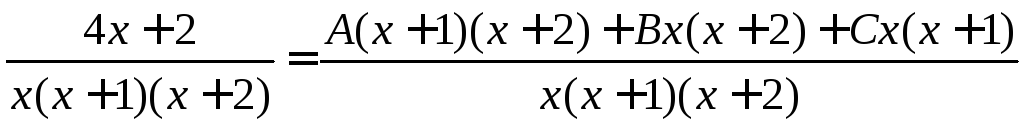Две дроби с одинаковыми знаменателями равны, если их числители равны

.

Полагая в последнем равенстве x равным корням знаменателя, получаем уравнения для нахождения коэффициентов А, В и С:

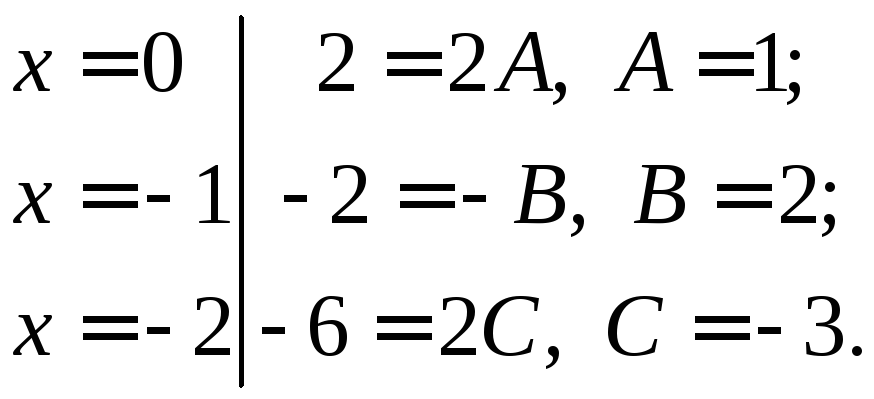
Итак, .

. ►

2. Вычислить .

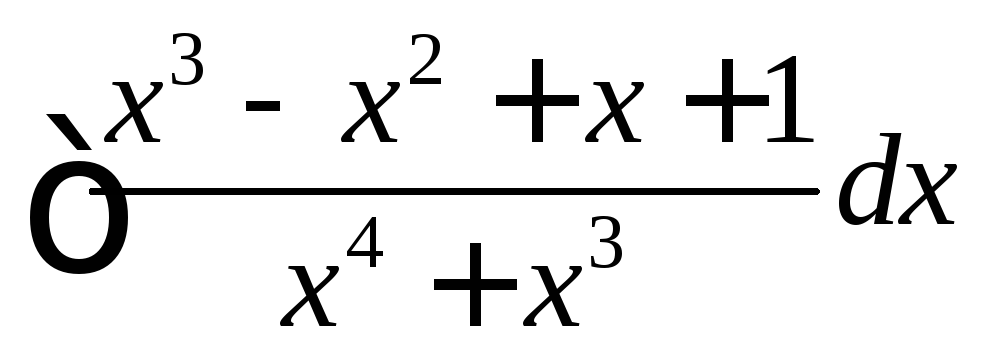◄ Дробь, стоящая под знаком интеграла, правильная. Её знаменатель разлагается на линейные множители:

.

Разложение дроби в сумму простейших ищем в виде

.

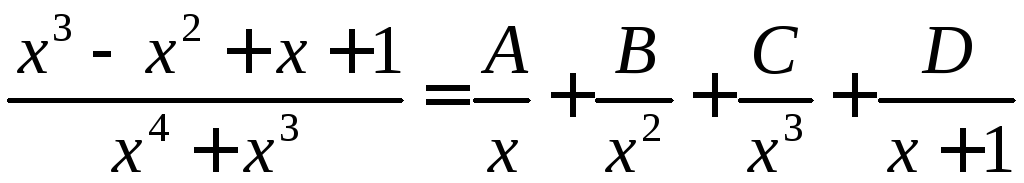Здесь первые три слагаемых соответствуют множителям x (их три), а четвёртое – множителю . Приводим правую часть этого равенства к общему знаменателю, равному, и приравниваем числители

или

.

Для нахождения неизвестных A, B, C, D используем равенство коэффициентов при одинаковых степенях x в многочленах, стоящих справа и слева от знака равенства.

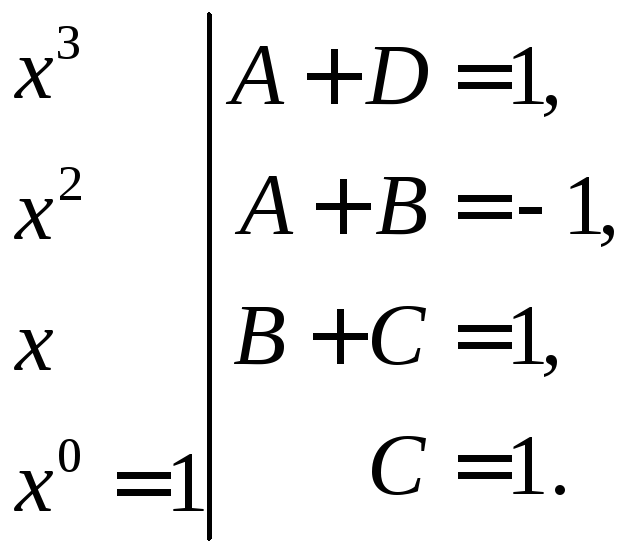
Поставляя найденные значения A, B, C, D в и интегрируя, получаем

. ►

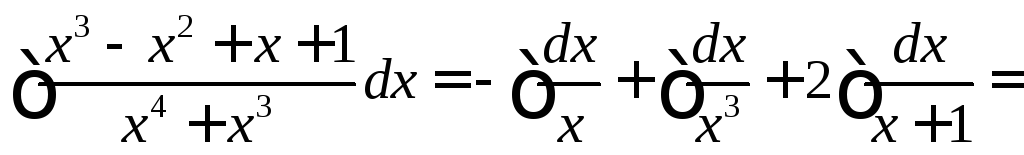
3. Вычислить .

◄ Дробь правильная. Знаменатель разлагается в произведение линейного и квадратичного множителей:. Так какв нуль не обращается, то на линейные множители уже не разлагается.

Ищем разложение дроби в сумму простейших дробей в виде

.

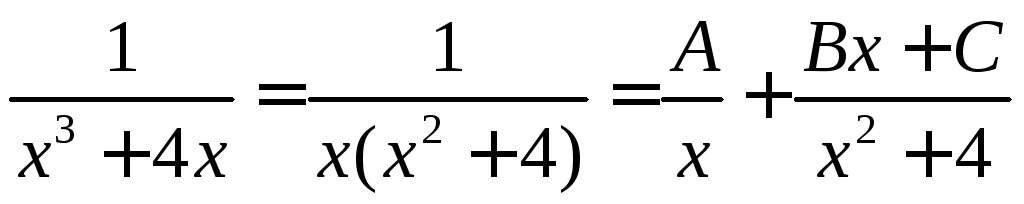Освободимся от знаменателя и найдём A, B и С, используя те же приёмы, что и в предыдущих примерах.

. .

.

.

Приравняем коэффициенты при одинаковых степенях x в многочленах, стоящих слева и справа от знака равенства: ,,. Отсюда,,. Таким образом,,

. ►

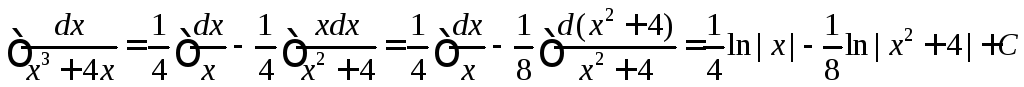4. Вычислить .

◄ Дробь, стоящая под знаком интеграла, неправильная, так как степень числителя больше степени знаменателя. Поэтому её надо представить в виде суммы многочлена (целой части) и правильной дроби, выполнив деление многочлена (числителя дроби) на многочлен (знаменатель дроби).

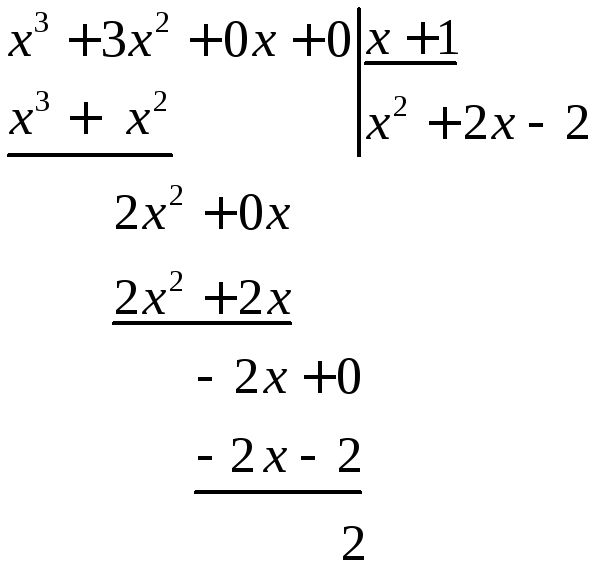
Итак, ,

. ►

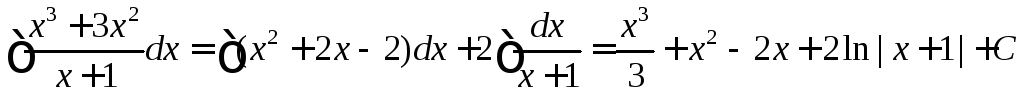3. Задачи для самостоятельного решения

Вычислить интегралы от рациональных дробей.

.	.
.	.
.	.

2. Интегралы от тригонометрических функций

1. Сведения из теории

1. Интегралы вида ,

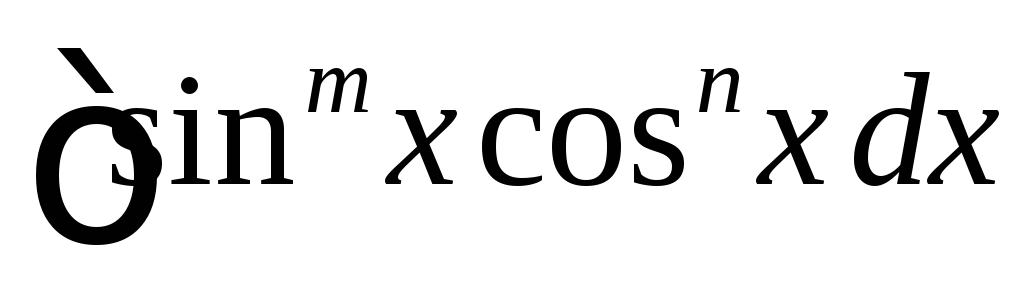где хотя бы одно из чисел m или n нечетное целое число

Пусть, например, – нечетно. Тогда

|| замена ||,

то есть интеграл сводится к сумме табличных интегралов от степеней.

2. Интегралы вида 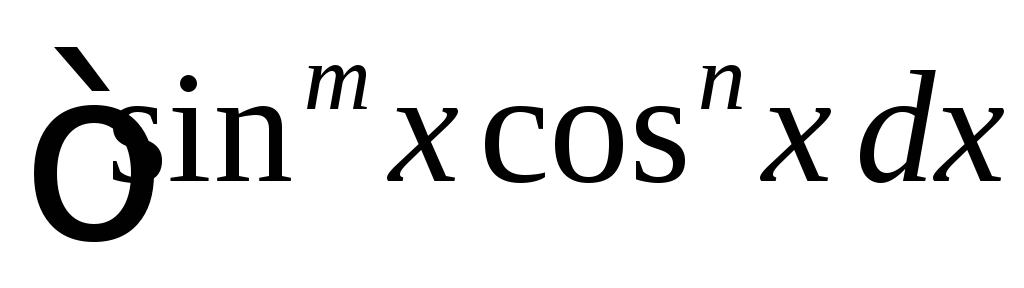, гдеm и n четные целые числа

Если m и n четные целые положительные числа, то используются формулы понижения степени

.

3. Интегралы от произведений синусов и косинусов

различных аргументов

Для их вычисления используются тригонометрические формулы

.

.

.

2. Примеры решения задач

1. Вычислить .

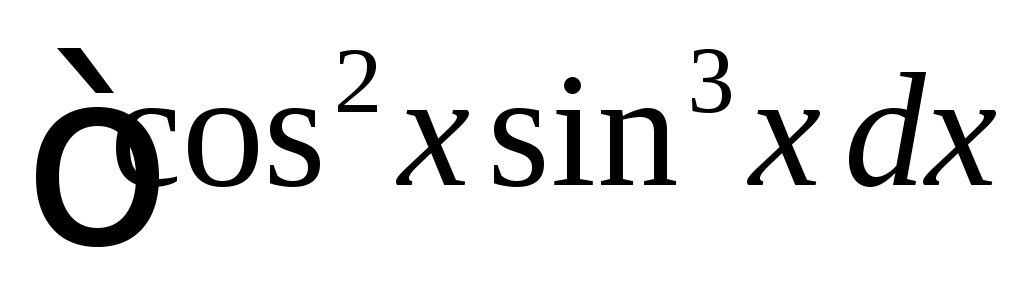◄ Так как стоит в нечетной степени, то

. ►

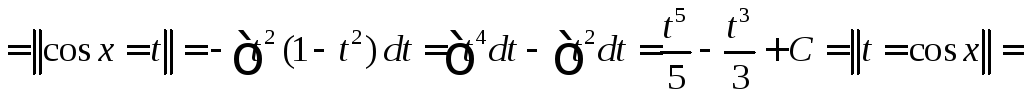
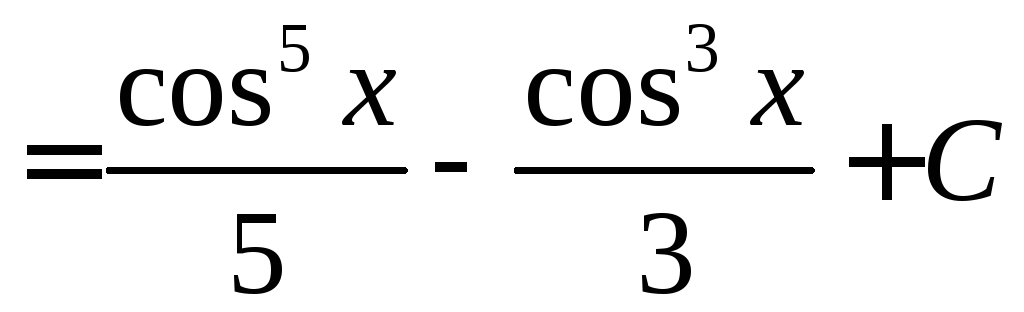2. Вычислить .

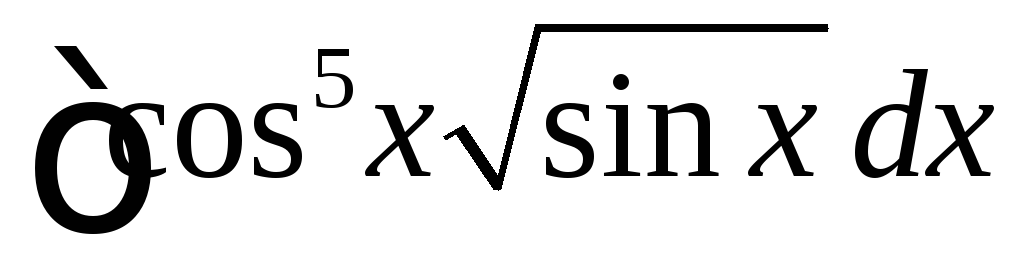◄ Используем то обстоятельство, что косинус стоит в нечётной степени.

=

=. ►

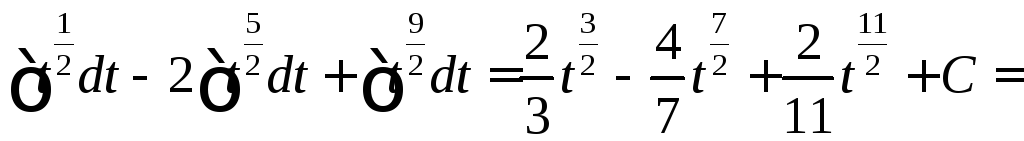
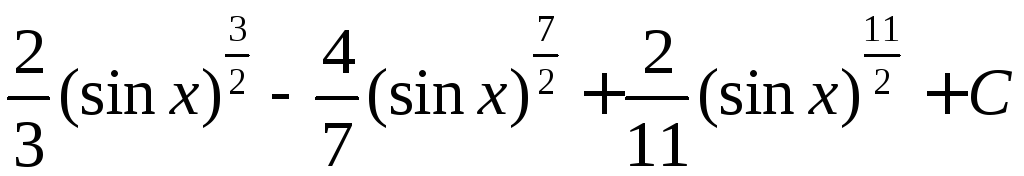3. Вычислить.

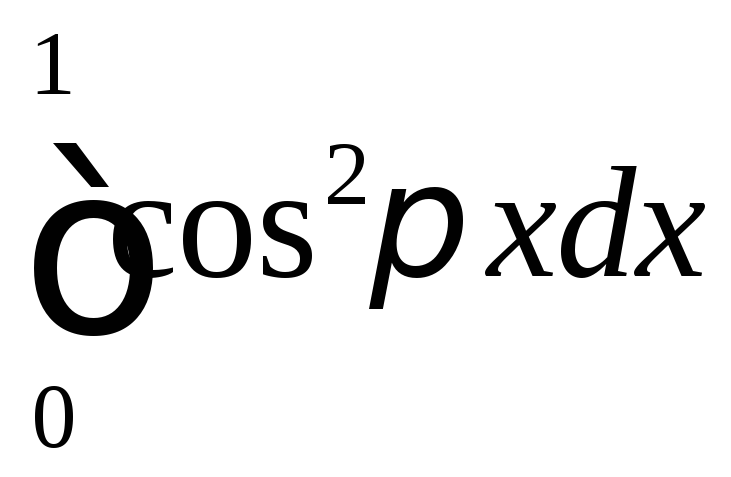◄ Используем вторую из формул понижения степени:

. ►

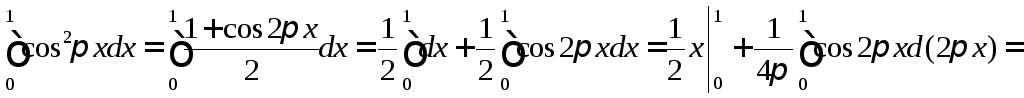
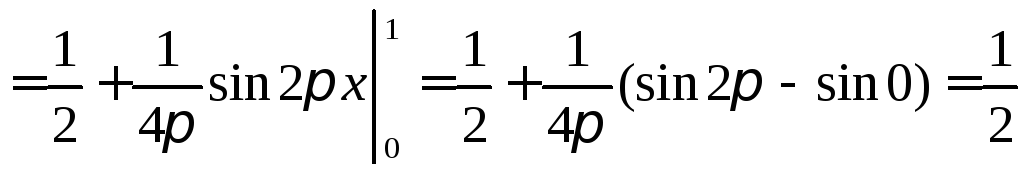4. Вычислить .

◄ Для вычисления этого интеграла от произведения синуса и косинуса в чётных степенях используем формулы понижения степени.

. ►

5. Вычислить .

◄ Используем формулу .

. ►

6. Вычислить .

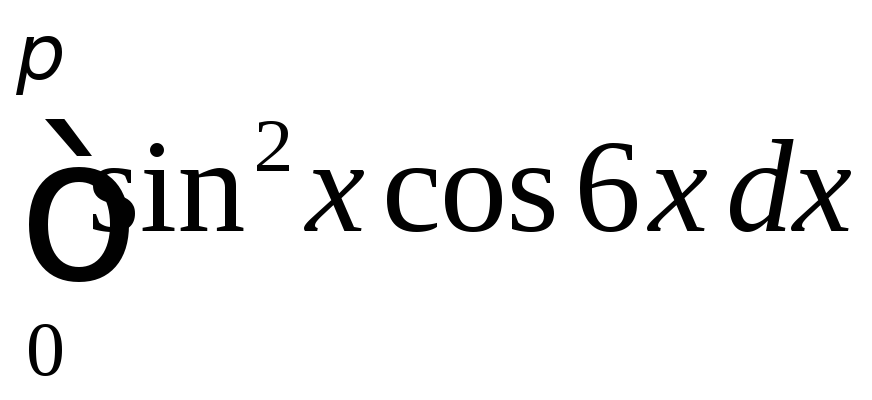◄ Избавляемся от квадрата по третьей из формул понижения степени, а затем используем формулу :

. ►

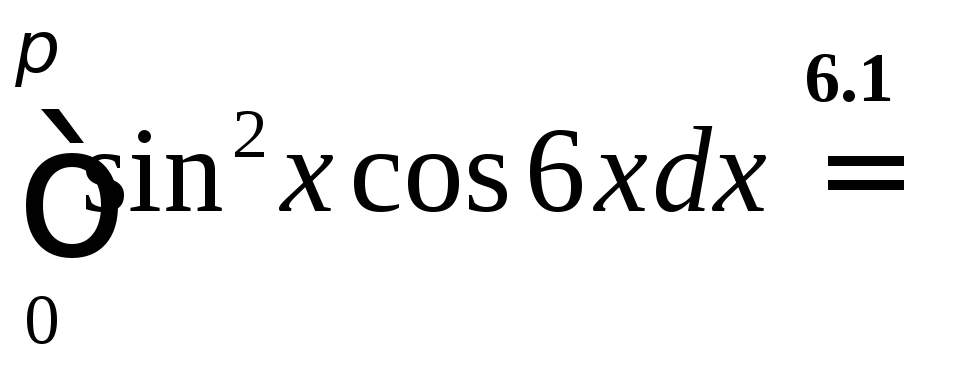
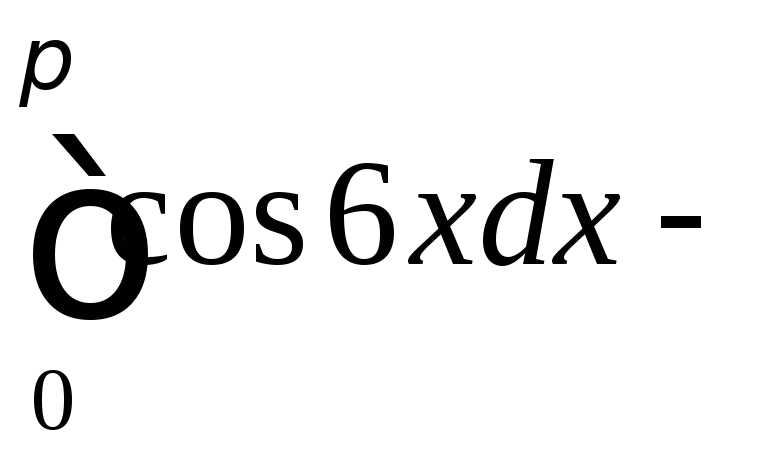
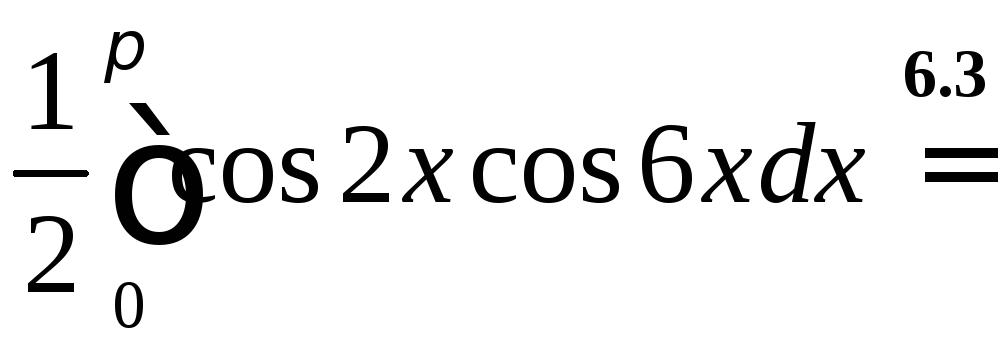
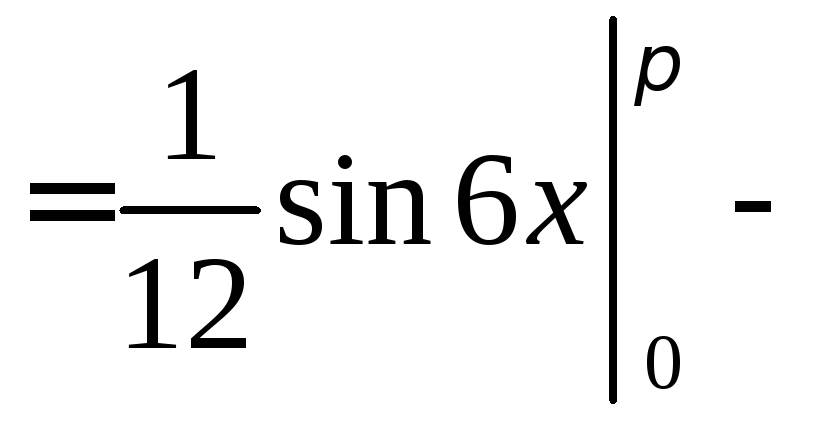
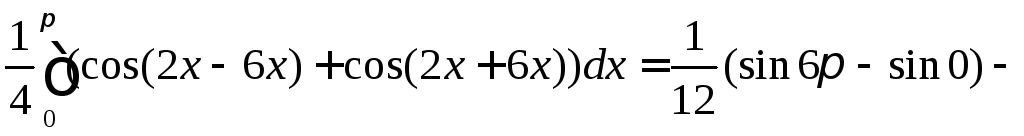
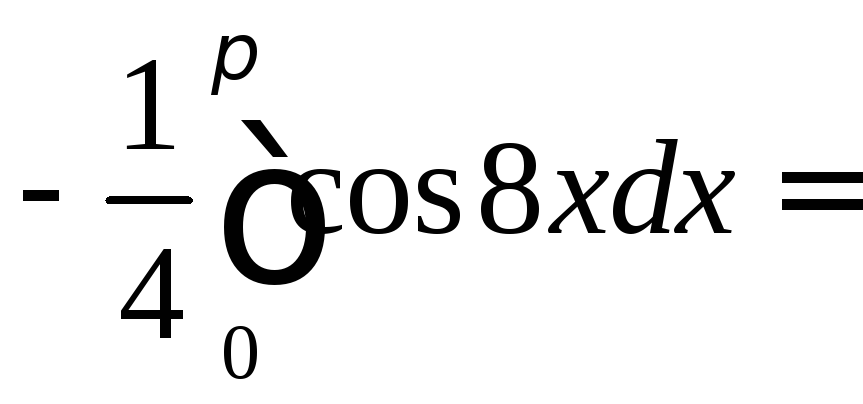
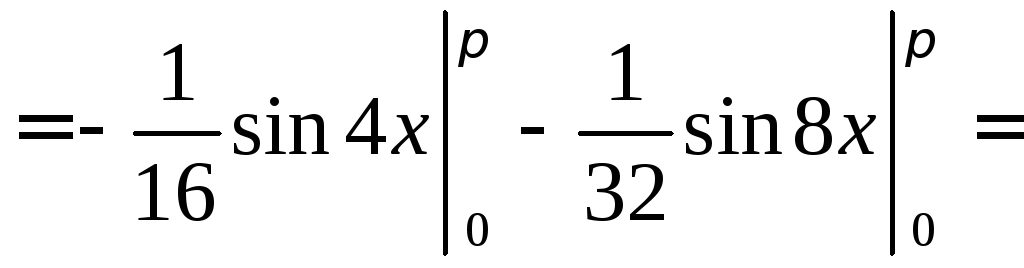
3. Задачи для самостоятельного решения

Вычислить интегралы

	.
.	.
.	.
.	.
.
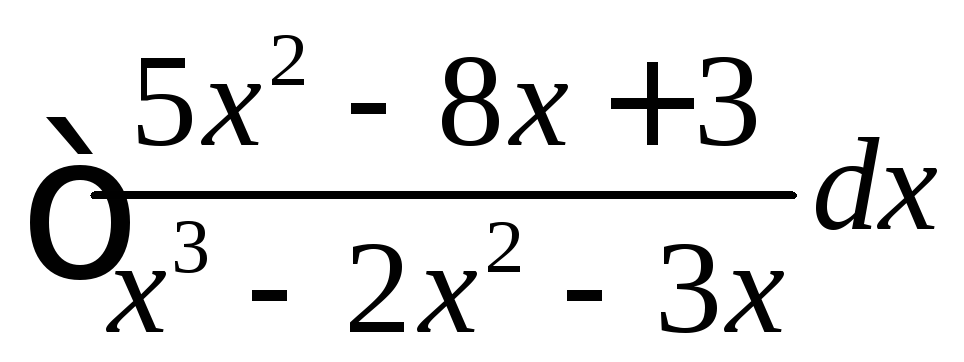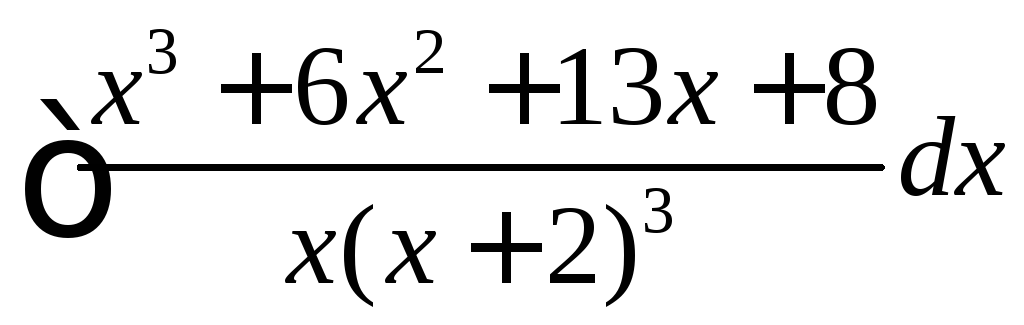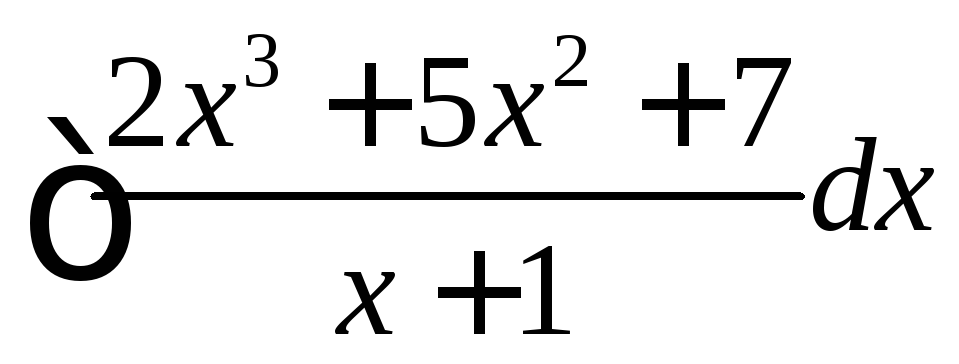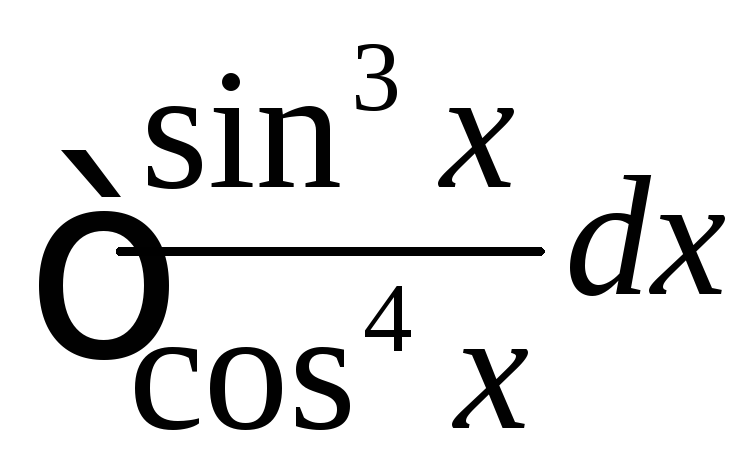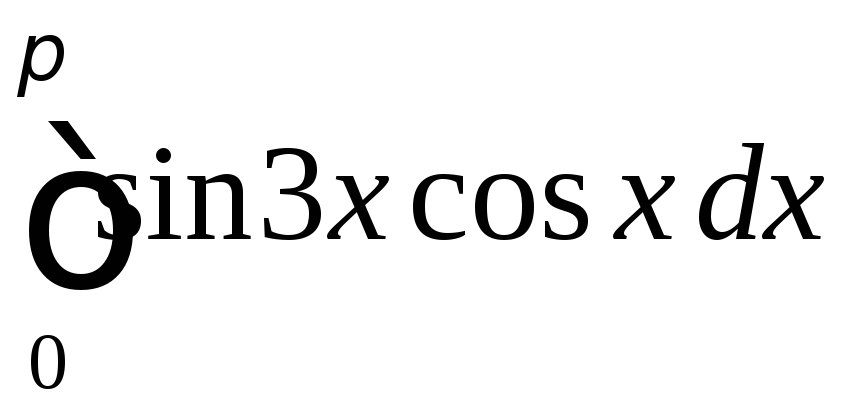