
- •Неопределенный и определенный интеграл
- •Понятия неопределенного и определенного интегралов. Таблица основных интегралов
- •Определенный интеграл. Формула Ньютона-Лейбница
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Метод замены переменных
- •Сведения из теории
- •Метод подведения под знак дифференциала
- •Метод подстановки
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Интегрирование по частям
- •Сведения из теории
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Примеры решения задач
- •Интегралы от тригонометрических функций
- •Несобственные интегралы
- •Задачи для самостоятельного решения
- •Библиографический список
- •Задания для контрольной работы
- •Учебное издание
Метод подстановки
Пусть
функция
![]() дифференцируема и имеет дифференцируемую
обратную
дифференцируема и имеет дифференцируемую
обратную![]() .
Тогда
.
Тогда
![]() ,
,
где
после вычисления интеграла, стоящего
в правой части этой формулы, надо заменить
переменную t
на функцию
![]() .
.
При
удачном выборе подстановки
![]() интеграл, стоящий в правой части формулы,
может оказаться «проще» исходного.
интеграл, стоящий в правой части формулы,
может оказаться «проще» исходного.
Для определенного интеграла соответствующая формула имеет вид
 ,
,
где
![]() ,
а
,
а![]() .
.
Примеры решения задач
Далее
знак
![]() будет означать ссылку на табличный
интеграл с номеромN.
будет означать ссылку на табличный
интеграл с номеромN.
Вычислить
 .
.
◄ Перепишем
интеграл в виде
![]() .
Под знаком интеграла стоит степень
функции
.
Под знаком интеграла стоит степень
функции![]() ,
поэтому удобно подвести
,
поэтому удобно подвести![]() под знак дифференциала:
под знак дифференциала:
![]()
 .
►
.
►
Вычислить
 .
.
◄ Подведём
под знак дифференциала
![]() :
так как дифференциал
:
так как дифференциал![]() ,
то
,
то![]() Поэтому
Поэтому

![]() .
.
Вычислить
 .
.
◄ Так
как
![]() и
и .
►
.
►
Вычислить
 .
.
◄ Так
как
![]() ,
то
,
то .
►
.
►
Вычислить
 .
.
◄ Так
как
![]() ,
то
,
то
![]() .
Тогда
.
Тогда

 .
►
.
►
Вычислить

 .
.
◄
Подведём
под знак дифференциала
![]() :
:
![]() .
►
.
►
Вычислить
 .
.
◄ Так
как
![]() ,
то
,
то![]() ,
тогда
,
тогда
![]()
![]() .
►
.
►
Вычислить
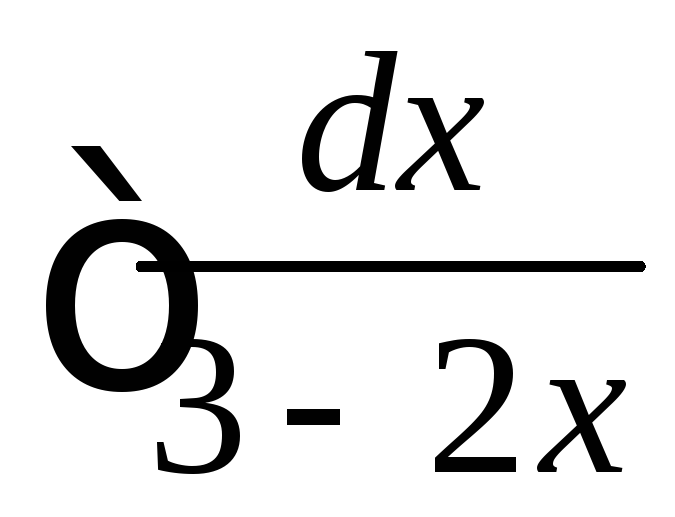 .
.
◄ Так
как
![]() ,
то
,
то
![]() .
►
.
►
Вычислить
 .
.
◄
 .
►
.
►
Вычислить
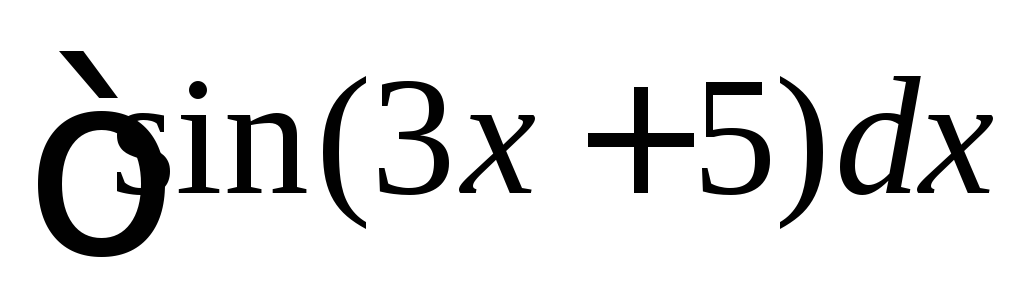 .
.
◄
![]()
![]()
![]() .
►
.
►
Вычислить
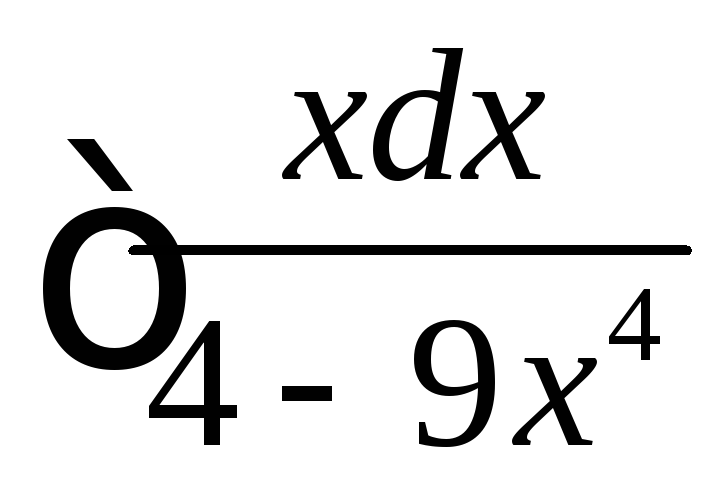 .
.
◄

 .
►
.
►
Вычислить
 .
.
◄

![]()
![]() .
►
.
►
Вычислить
 .
.
◄ Так как интеграл определенный, то будем пользоваться вариантом формулы подведения под дифференциал.



 .
►
.
►
Вычислить
 .
.
◄


![]()
![]()
![]() .
►
.
►
Вычислить
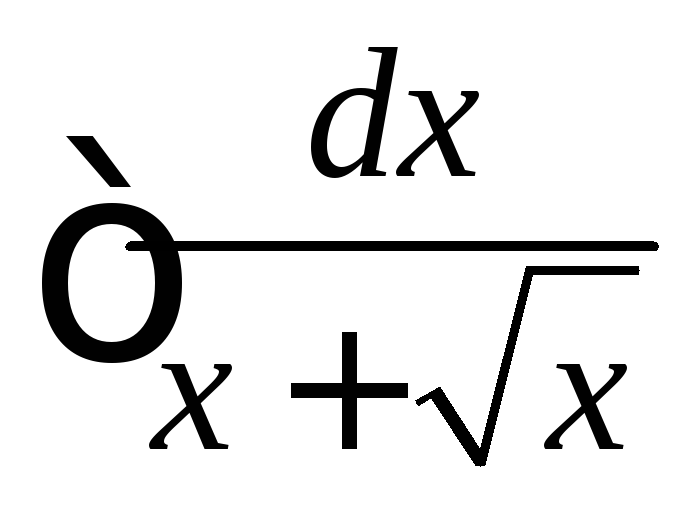 .
.
◄ Будем
пользоваться формулой замены переменных
в форме подстановки. Обозначим
![]() .
Тогда
.
Тогда![]() ,
,![]() и
и
 .
►
.
►
Вычислить
 .
.
◄ Так
как интеграл определенный, то воспользуемся
формулой замены переменных. Обозначим
![]() .
Тогда
.
Тогда![]() при
при
![]() ,
,
![]() при
при![]() ,
,![]() ,
,![]() ,
и
,
и

 .
►
.
►
Задачи для самостоятельного решения
Вычислить интегралы, используя метод подведения под знак дифференциала.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислить интегралы, применяя указанные подстановки.
|
|
|
|
|
|

 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. .
. ,
,