3.2 Случайная векторная величина двух измерений

На практике решаются задачи, в которых результат опыта описывается не одной с.в., а двумя или более с.в., образующими систему. При этом свойства системы нескольких с.в. могут включать и взаимные связи (зависимости) между ними.

Е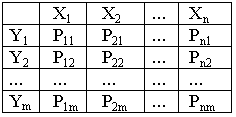сли с.в.XиYпринимают дискретные значенияx_i,y_jи каждой паре значений (x_i,y_j) соответствует определенная вероятностьp_ij, то можно составить таблицу распределения вероятностей дискретной двумерной с.в.

Очевидно .

Значение функции Р(x,y)равно вероятности обнаружить с.в.Х<хи с.в.Y<y, т.е.

P(x,y)=Prob(X<x,Y<y).

Свойства функции распределения Р(x,y):

1) Р(х,y) - неубывающая функция своих аргументов,

т.е. при х₂>x₁ P(x₂,y)>P(x₁,y)или приy₂>y₁ P(x,y₂)>P(x,y₁);

2) P(x,-)=P(-,y)=P(-,-)=0;

3) P(x,+)=P(x), P(+,y)=P(y)- если один из аргументов равен +, то функция распределенияР(х,y)превращается в функцию распределения другой с.в.;

4) P(+,+)=1.

Плотность распределения системы двух с.в. (вторая смешанная производная P(x,y)пои затем по).

(25.3)(15.3)

или в общем виде

, .

Геометрически p(x,y)можно представить поверхностью (поверхность распределения - поОХиOYоткладываются значения с.в.X и Y, по Z- вероятность их появления, см. рис. ).

Из (25) следует

(26.3)(17.3).

Вероятность обнаружить двумерную с.в. (X,Y)в областиD:

Prob((X,Y)D)= (27.3)=(16.3).

Вероятность обнаружить точку Мс координатамих₁,х₂,...х_nвn-мерном объемеV:

Prob(MV)=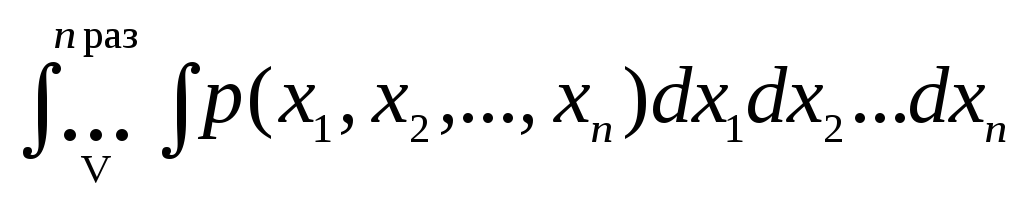 (27.3)

Далее, аналогично (18)

(28.3),

т.е. геометрически объем под поверхностью распределения равен 1.

В общем виде имеем n-кратный интеграл

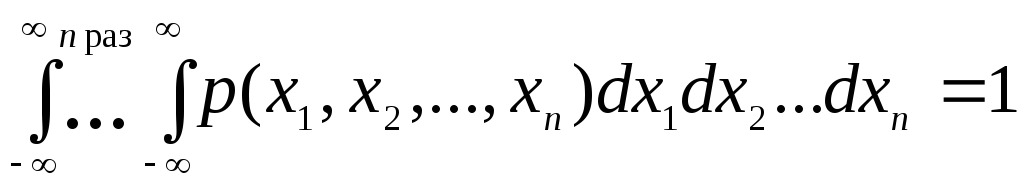(28.3).

Если известен закон распределениясистемы двух случайных величин p(x,y), то можно определить законы распределения отдельных величин, входящих в систему:

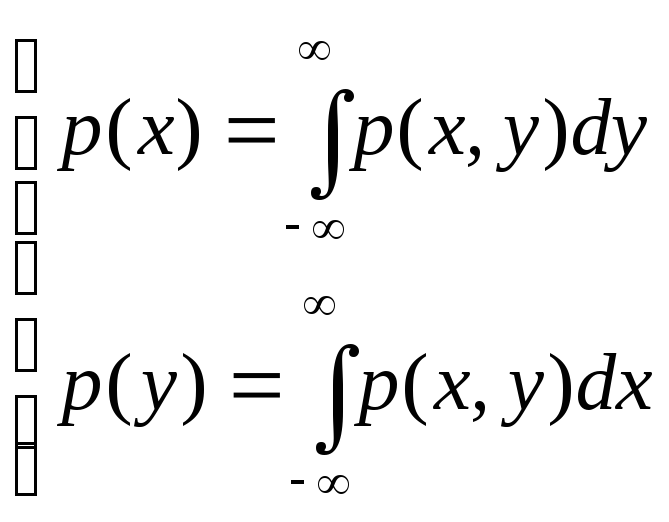(29.3).

То же, в общем виде:

(29.3).

Но для того, чтобы по заданным законам распределения отдельных с.в., входящих в систему, определить законы распределения системы с.в., надо знать зависимость между величинами, входящими в систему.

Условный закон распределения с.в.Х, входящей в систему (X,Y) - закон ее распределения, вычисленный при условии, что другая с.в. Y приняла определенное значение. Условный закон распределения можно задавать функцией P(x/y) и плотностью p(x/y) распределения.

Геометрически функция плотности распределения p(x/y) представляет собой сечение поверхности распределения при y=const. Сечения поверхности распределения плоскостями x=const и y=const дают соответственно условные плотности распределения p(y/x) величины Y при определенных значениях x и условные плотности распределения p(x/y) величины X при определенных значениях y. Если X и Y - зависимые с.в., то кривые плотности распределения p(y/x) изменяются при изменении x, а кривые плотности распределения p(x/y) изменяются при изменении y. М.о. этих кривых при таких изменениях образуют линии регрессии 1 и 2. В случае независимости X и Y линии регрессии представляют собой прямые и, параллельные осям координат. При наличии функциональной связи (а не стохастической) междуX и Y обе линии регрессии сливаются в одну - y=y(x), при этом поверхность плотности распределения может быть заменена кривой плотности распределения X или Y вдоль линии y=y(x).

С учетом вышесказанного плотность распределения системы двух с.в. равна плотности распределения одной из них, умноженной на условную плотность распределения другой величины, вычисленную при условии, что первая величина приняла заданное значение:

p(x,y)=p(x)p(y/x) (30.3)=(7.2)

или в общем случае

p(x₁,x₂,...,x_n)=p(x₁,x₂,...,x_i/x_i+1,x_i+2,...,x_n)p(x_i+1,x_i+2,...,x_n) (30.3).

Для независимых с.в. p(x,y)=p(x)p(y) (31)=(3) - плотность распределения системы независимых с.в. равна произведению плотностей распределения отдельных величин, входящих в систему.