Контрольные вопросы

1. Какова структура общего решения неоднородного дифференциального уравнения с постоянными коэффициентами?

2. От чего зависит и как находится частное решение неоднородного дифференциального уравнения с постоянными коэффициентами?

3.Как находится частное решение неоднородного дифференциального уравнения с постоянными коэффициентами, удовлетворяющее начальным условиям?

Тема 14. Ряды. Знакоположительные числовые ряды

14.1. Числовые ряды. Сходимость числовых рядов

Пусть дана некоторая бесконечная последовательность чисел . Сумма всех этих чиселa₁+a₂+a₃… +a_n+ … называется числовым рядом или просто рядом. Числаназываются членами ряда, член– общим членом ряда. Кратко числовой ряд записывают с помощью знака суммы, так: .

Сумма нескольких первых подряд членов ряда называется частичной суммой. Они обозначаются следующим образом:

.

Ряд называется сходящимся, если последовательность его частичных сумм сходится к какому-нибудь числу , которое называется суммой ряда, то есть. Если последовательность частичных сумм расходится, то ряд называется расходящимся.

В качестве примера рассмотрим ряд, составленный из членов геометрической прогрессии с первым членом и знаменателем:

.

Если , то частичная сумма этого ряда находится по формуле:

.

Если , то для значений, и тогда получаем, что

,

то есть ряд будет сходиться. В случае если для значенийи последовательностьне имеет конечного предела, то есть ряд в этом случае будет расходиться.

Ряд называется гармоническим. Покажем, что этот ряд расходится. Для этого из последовательности его частичных сумм выделим суммы с номерамии сделаем их оценку:

,

,

.

Для любого получим:

и для значений . Поэтому последовательностьне имеет конечного предела.

В экономике бесконечные ряды и их суммы применяются, например, для решения следующей задачи. Владелец бессрочной облигации номиналом 1000 рублей каждый год получает 30 рублей. Определить истинную цену всей этой бесконечной последовательности платежей, если инфляция составляет 2% в год.

С учетом инфляции через год полученные 30 рублей сейчас будут эквивалентны рублям, через два годарублям и так далее. В итоге получаем сумму бесконечно убывающей геометрической прогрессии.

14.2. Свойства сходящихся рядов. Необходимый признак сходимости ряда

В следующей теореме указываются свойства сходящихся рядов.

Теорема.Если,,, то.

Итак, сходящиеся ряды можно почленно складывать, вычитать, умножать на одно и то же произвольное число, при этом получаются сходящиеся ряды. Для получения их суммы надо суммы исходных рядов соответственно складывать, вычитать, умножать на это число.

Добавление к ряду конечного числа слагаемых или отбрасывание в нем конечного числа слагаемых на сходимость или расходимость ряда не влияет, при этом, если ряд сходится, то его сумма изменится на ту величину, которая добавлена или отброшена.

Установить сходимость или расходимость ряда путем определения и вычислениявозможно не всегда. Проще это можно сделать, используя признаки сходимости. Необходимый признак сходимости ряда выражает следующая теорема.

Теорема.Если рядсходится, то предел его общего членадля значенийравен нулю, то есть

.

Это условие является необходимым, но не достаточным условием сходимости ряда. Например, для гармонического ряда предел его общего члена равен нулю, но, как было установлено выше, гармонический ряд, является расходящимся.

Если же для некоторого ряда предел его общего члена не стремится к нулю, то теорема сразу позволяет сказать, что такой ряд расходится. Например, исследовать сходимость ряда . Найдем предел общего члена этого ряда:

,

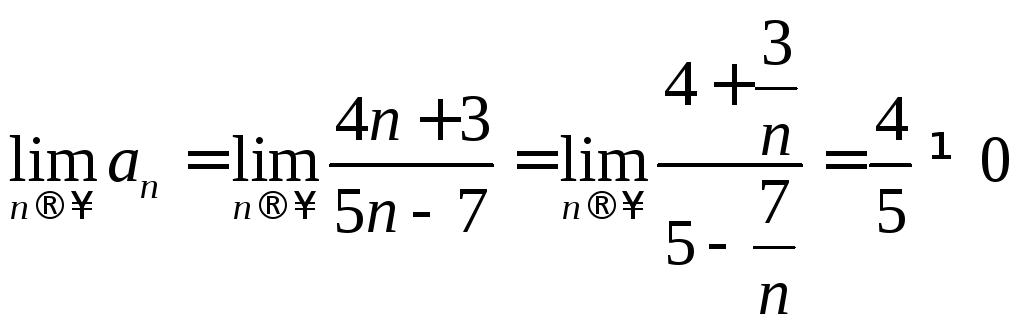то есть необходимый признак не выполняется, ряд расходится.