116 117
Тема 13. Неоднородные линейные
дифференциальные уравнения
второго порядка
с постоянными коэффициентами
13.1. Структура решения неоднородного линейного
дифференциального уравнения второго порядка
с постоянными коэффициентами
Уравнение вида
,
где pиq– вещественные числа, называется линейным неоднородным уравнением второго порядка с постоянными коэффициентами.
Общее решение этого уравнения представляет собой сумму частного решения неоднородного уравнения yч.н.и общего решения соответствующего однородного уравненияyо.о., то естьy=yч.н.+yо.о.. Это утверждение составляет содержание теоремы о структуре общего решения неоднородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами.
Напомним, уравнение является однородным,
если f(x)
равно нулю. Для того чтобы решить
однородное дифференциальное уравнение,
необходимо составить характеристическое
уравнение
.
При его решении возможны следующие три
случая.
Случай 1. Если корни k1,k2 различны, то общее решение однородного уравнения имеет вид:
.
Случай 2. Если k1 =k2 =k, то общее решение однородного уравнения имеет вид:
.
Случай 3. Если
,
то общее решение однородного уравнения
имеет вид:
,
где
,
.
13.2. Нахождение частных решений неоднородных линейных дифференциальных уравнений второго порядка с постоянными коэффициентами
Частное решение линейного неоднородного
уравнения зависит от вида правой части
уравнения, то есть от функции
.
Если
,
где
–данный многочлен степени
,
то частное решение линейного неоднородного
уравнения имеет вид:
,
где
– многочлен степени
с неизвестными коэффициентами, которые
нужно найти,
– число корней характеристического
уравнения, равных нулю.
Если
,
то частное решение линейного неоднородного
уравнения имеет вид:
,
где
– многочлен степени
с неизвестными коэффициентами,
– кратность корня характеристического
уравнения
.
Если
,
где
,
и
– известные числа, то частное решение
линейного неоднородного уравнения
имеет вид:
где
,
– неизвестные коэффициенты,
– число корней характеристического
уравнения, равных
.
13.3. Примеры решений неоднородных линейных дифференциальных уравнений второго порядка с постоянными коэффициентами
Рассмотрим примеры решения неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами.
Пример 1.Найти общее решение уравнения
.
Решение.Характеристическое уравнение
имеет корниk1 =
0,k2 = 1. Общее
решение однородного уравнения тогда
имеет вид:
.
Найдем частное решение неоднородного уравнения. Так как 0 является корнем характеристического уравнения кратности т = 1, то частное решение имеет вид:
.
Найдем
и
:
,
.
Теперь подставим производные в исходное уравнение, получим:
.
Приравнивая коэффициенты при одинаковых
степенях
,
получим систему алгебраических уравнений:
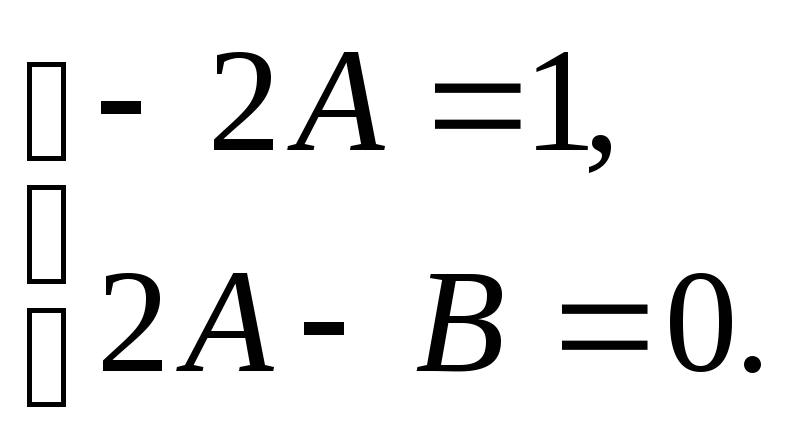
Решая систему, находим, что
,
.
Итак,
.
Тогда общее решение неоднородного
уравнения примет вид:
.
Пример 2.Найти общее решение уравнения
.
Решение. Характеристическое уравнение
имеет вид:
,
которое имеет корниk1
= 2,k2 = 3.
Следовательно, общее решение однородного
уравнения примет вид:
.
Так как
= 1 не является корнем характеристического
уравнения, то частное решение неоднородного
уравнения необходимо искать в виде:
.
Подставив
и
в исходное уравнение, получим:
;
;
;
.
Приравняем коэффициенты при одинаковых
степенях
,
получим систему уравнений:
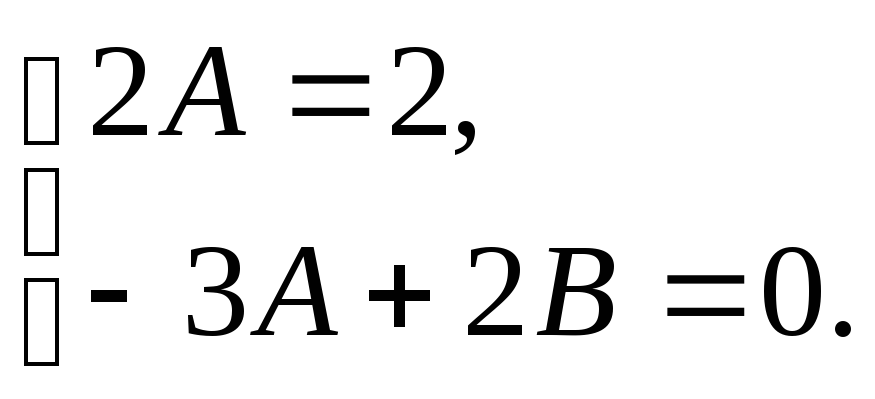
Откуда находим, что
,
.
Находим общее решение неоднородного уравнения:
Пример 3.Найти частное решение
уравнения
,
удовлетворяющее начальным условиям
,
.
Решение. Характеристическое уравнениеk2+ 1 = 0 действительных
корней не имеет. Найдем
и
:
,
.
Общее решение однородного уравнения имеет вид:
.
Найдем частное решение неоднородного уравнения. Так как 2 не является корнем характеристического уравнения, то
;
;
.
Подставим
и
в исходное уравнение, получим:
;
.
Из последнего равенства получим систему уравнений:
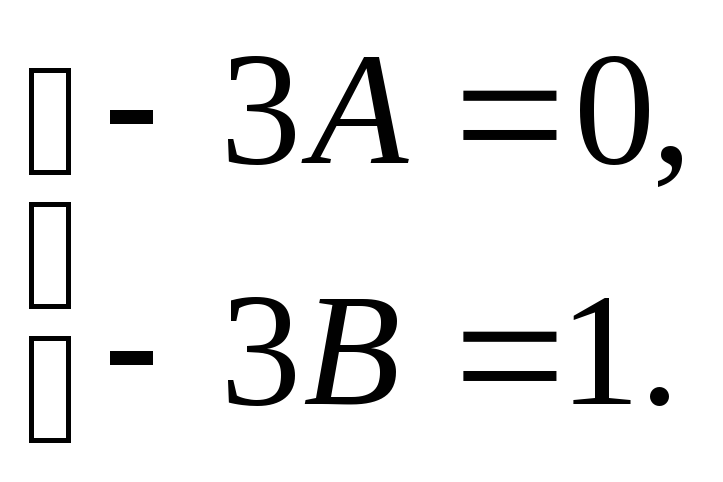
Откуда следует, что
,
.
Тогда общее решение неоднородного уравнения имеет вид:
.
Для того чтобы найти частное решение исходного уравнения, подставим начальные условия в полученное решение. Имеем:
,
.
,
,
.
Тогда получаем, что частное решение,
удовлетворяющее начальным условиям
,
,
имеет вид:
.