1.2. Множество действительных чисел

Числа, используемые для счета, образуют множество натуральных чисел, обозначается .

Натуральные числа, им противоположные, а также число нуль составляют множество целых чисел. Оно обозначается .

Рациональными называются числа, представимые в виде , где,. В десятичной системе счисления рациональные числа представляются в виде конечной или периодической десятичной дроби,. Множество рациональных чисел обозначается.

Иррациональными называются числа, представимые в виде бесконечной непериодической десятичной дроби. Любые иррациональные числа можно как угодно точно приближать конечными десятичными дробями. Например, ,,,,, …

Рациональные и иррациональные числа образуют множество действительных или вещественных чисел, обозначается . Очевидно.

Действительные числа геометрически изображаются точками числовой прямой (или числовой оси), т.е. прямой, на которой выбрано начало отсчета, положительное направление и единица масштаба. Каждому действительному числу числовой прямой соответствует определенная точка. Это число называют координатой точкии обозначают.

Множество Х, элементы которого удовлетворяют неравенству, называется отрезком (или сегментом); неравенству– интервалом; неравенствамили– полуинтерваламии. Также рассматриваются бесконечные интервалы и полуинтервалы:,,,,. Указанные множества объединяют термином «промежуток».

1.3. Комплексные числа. Действия над комплексными числами

Комплексные числа возникли при решении квадратных уравнений. Квадратное уравнение, дискриминант которого меньше нуля, во множестве действительных чисел решения не имеет. Уравнение будет иметь решение, если. Числообозначаюти называют мнимой единицей.

Комплексным числом называется выражение вида:

,

где – действительные числа,– мнимая единица. Числоназывается действительной частью числа, а число– мнимой частью. Действительное числоявляется частным случаем комплексного числапри. Множество комплексных чисел обозначается. Очевидно.

Запись комплексного числа в виде

называется алгебраической формой комплексного числа.

Числа иназываются сопряженными. Два комплексных числа называются равными, если равны их действительные и мнимые части.

Арифметические операции над комплексными числами иопределяются из правил сложения и умножения многочленови, если считать:

Сумма (разность) комплексных чисел:

.

1. Произведение комплексных чисел:

2. Деление двух комплексных чисел и, где:

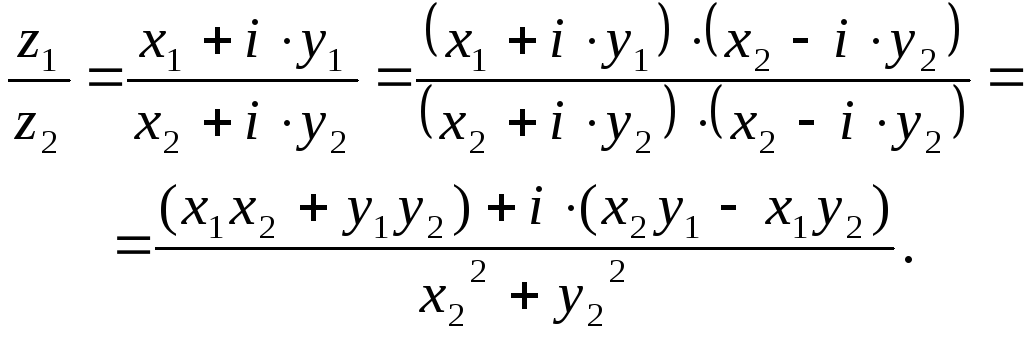
Для изображения комплексных чисел служат точки координатной плоскости. Осии, на которых расположены действительные числаи чисто мнимые, называются соответственно действительной и мнимой осями. В этом случае точка с координатамизадает комплексное число, а сама плоскость называется комплексной.

С каждой точкой комплексной плоскости связан радиус-вектор, длина которогоназывается модулем комплексного числаи обозначается. Угол, образованный радиус-векторомс осью, называется аргументом комплексного числа и обозначается.

Из прямоугольного треугольника получаем:

,,,

т.е. ,.

Следовательно, комплексное число можно представить в виде. Такой вид называется тригонометрической формой комплексного числа.

Формулы Эйлера преобразуют тригонометрическую форму комплексного числа в показательную форму:

.

Сложение и вычитание комплексных чисел удобнее выполнять в алгебраической форме, умножать и делить эти числа удобнее, используя тригонометрическую или показательную форму записи комплексных чисел и:

,

,

,

.

Возведение в степень комплексного числа и извлечение корня из этого числа производится по следующим формулам:

,