7.2. Исследовать линейный вид зависимости

Модель регрессии может быть построена по сгруппированным данным (Таблицы 12). Для выявления связи между признаками по достаточно большому количеству наблюдений используется корреляционная таблица. В корреляционной таблице можно отобразить только парную связь, т.е. парную связь результативного признака только с одним фактором, и на её основе построить уравнение регрессии и определить показатель тесноты связи.

Для составления корреляционной таблицы парной связи статистические данные необходимо сгруппировать по обоим признакам, затем построить таблицу, по строкам отложить группы результативного, а по столбцам - группы факторного признака.

Таблица 12. Сгруппированные данные.

среднегодовая стоимость ОФ	х	ФЗП				fy		yfy		xyfy
		33,6-278,2	278,2-417,3	417,3-450,9
	у	155,9	347,75	434,1
179,6-429,9	304,75	13	-	-	13		3961,75		617636.83
429,9-680,2	555,05	7	-	-	7		3885,35		1351130.46
680,2-930,5	805,35	1	3	2	6		4832,1		2097614.61
fx		21	3	2
xfx		3273,9	1043,25	868,2
x2fx		510401,01	362790,1875	376885,62

Корреляционная таблица даёт общее представление о направлении связи. В нашем случае связь прямая.

Для определения коэффициентов уравнения воспользуемся системой нормальных уравнений вида:

a₀=-1199.6

a₁=8.2

Уравнение регрессии имеет вид:

y=8.2*x-1199.6

Задание 8. Сравнить и проанализировать результаты расчётов пунктов 5, 6, 7.

В задании 5 по результатам простой группировки была определена взаимосвязь между среднегодовой стоимостью основных фондов и фондом заработной платы с использованием дисперсий. Для этого был подсчитан коэффициент детерминации и эмпирическое корреляционное отношение. Коэффициент детерминации равный 98,66% позволил сделать вывод о том, что изменение среднегодовой стоимости основных фондов влияет на изменение фонда заработной платы на 98,66%

Эмпирическое корреляционное отношение равное 0,9932 дало возможность судить о том, что связь между среднегодовой стоимостью основных фондов фондом заработной платы тесная и прямая, т.к. значение этого отношения положительно и близко к единице.

В задании 6 теснота связи между данными показателями определяется с помощью ранговой корреляции. Значение коэффициента ранговой корреляции равно 0.753. Это говорит о том, что связь между среднегодовой стоимостью основных фондов и фондом заработной платы прямая и тесная, т.к. чем ближе по абсолютной величине коэффициент корреляции рангов к 1, тем теснее связь.

В задании 7 теснота парной связи и форма связи между исследуемыми признаками определяется методом корреляционно-регрессивного анализа. При исследовании линейной зависимости уравнение регрессии имело вид:

у=141,421+1,711*x

Положительное значение коэффициента а₁ говорит о том, что связь между исследуемыми признаками прямая, т.е. увеличение факторного признака ведет за собой увеличение и результативного. Значение линейного коэффициента корреляции равное 0,9199 говорит о наличии прямой тесной связи между среднегодовой стоимостью основных фондов и фондом заработной платы.

В качестве оптимальной математической функции, адекватно отражающей эмпирические данные, я решила выбрать линейную функцию. Уравнение степенной регрессии имеет вид: y=22.76*x^0.61, а₁>0, следовательно связь прямая.

Полученный индекс корреляции (r_xy=0.995) свидетельствует о том, что связь тесная прямая между среднегодовой стоимостью основных фондов и фондом заработной платы.

Таким образом, сравнив результаты расчётов, полученных в задании 5,6,7 можно сделать следующие выводы, что между среднегодовой стоимостью основных фондов и фондом заработной платы существует прямая тесная связь.

Результаты расчётов коэффициентов, характеризующих тесноту связи в заданиях 5, 6, 7 свидетельствует о наличии тесной прямой связи, не противоречат друг другу и незначительно отличаются друг от друга.

Задание 9. Исследовать тесноту линейной множественной связи между результативным признаком (фонд заработной платы) и двумя факторными (среднегодовая стоимость ОФ и среднемесячная з/п работника предприятия)

Статистическая модель, показывающая связь между результативным и несколькими факторными признаками, представляет собой уравнение множественной регрессии. Для исследования тесноты линейной множественной связи между результативным признаком среднегодовая стоимость основных фондов и двумя факторными: среднегодовая стоимость ОФ и среднемесячная з/п работника предприятия, рассмотрим множественное уравнение связи:

у=а0+а1х1+а2х2

Параметры этого уравнения определяются решением системы нормальных уравнений, составленных в результате применения метода наименьших квадратов:

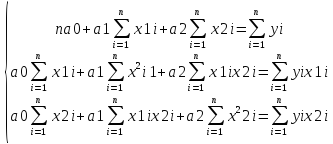
Для определения параметров системы составим вспомогательную таблицу (Таблица 13).

Получаем параметры уравнения:

a₀=-43.62

a₁=0.49

a₂=0.000161

Следовательно, множественное уравнение регрессии выглядит следующим образом:

y=-43.62+0.49x₁+0.000161x₂

Таблица 13. Вспомогательная таблица для определения параметров системы

№ пред-прия-тия	Фонд заработной платы	Среднегодо-вая стоимость основных фондов,	Среднемесячная з/п сотрудника предприятия x2i	x21i	x22i	x1i*x2i	yi*x1i	yi*x2i	y2
	Yi	x1i
1	33,6	180,1	16969,7	32436,01	287970718,1	3056242,97	6051,36	570181,92	1128,96
2	63,2	294,5	23617,34	86730,25	557778748,7	6955306,63	18612,4	1492615,89	3994,24
3	241	420,8	36850,15	177072,6	1357933555	15506543,12	101412,8	8880886,15	58081
4	275,3	469,7	37982,89	220618,1	1442699933	17840563,43	129308,4	10456689,6	75790,09
5	159,7	426,9	29313,51	182243,6	859281868,5	12513937,42	68175,93	4681367,55	25504,09
6	209	552,4	34556,88	305145,8	1194177955	19089220,51	115451,6	7222387,92	43681
7	251,8	664,6	37672,05	441693,2	1419183351	25036844,43	167346,3	9485822,19	63403,24
8	286,3	784,2	39370,19	614969,6	1550011861	30874103	224516,5	11271685,4	81967,69
9	149,3	341,8	28148,57	116827,2	792341993	9621181,226	51030,74	4202581,5	22290,49
10	93,4	438	36370,72	191844	1322829273	15930375,36	40909,2	3397025,25	8723,56
11	406,9	825,4	48165,25	681285,2	2319891308	39755597,35	335855,3	19598440,2	165567,6
12	80,6	179,8	36503,62	32328,04	1332514273	6563350,876	14491,88	2942191,77	6496,36
13	278,2	551,5	40318,84	304152,3	1625608859	22235840,26	153427,3	11216701,3	77395,24
14	70,9	323,4	26614,11	104587,6	708310851,1	8607003,174	22929,06	1886940,4	5026,81
15	92	354,2	23092,37	125457,6	533257552,2	8179317,454	32586,4	2124498,04	8464
16	260,8	551,9	37342,5	304593,6	1394462306	20609325,75	143935,5	9738924	68016,64
17	71,6	228,3	19627,19	52120,89	385226587,3	4480887,477	16346,28	1405306,8	5126,56
18	191	367,4	31769,79	134982,8	1009319557	11672220,85	70173,4	6068029,89	36481
19	450,9	930,3	49966,76	865458,1	2496677105	46484076,83	419472,3	22530012,1	203310,8
20	120,5	179,6	54872,5	32256,16	3010991256	9855101	21641,8	6612136,25	14520,25
21	79,7	404,8	31477,09	163863	990807194,9	12741926,03	32262,56	2508724,07	6352,09
22	175,5	473,3	31384,12	224012,9	984962988,2	14854104	83064,15	5507913,06	30800,25
23	38,1	180,4	16978,61	32544,16	288273197,5	3062941,244	6873,24	646885,041	1451,61
24	417,4	828,3	48921,71	686080,9	2393333709	40521852,39	345732,4	20419921,8	174222,8
25	343,9	862,8	43095,24	744423,8	1857199711	37182573,07	296716,9	14820453	118267,2
Итого	4841	11814	860981,7	6857727	32115045711	443230435,9	2918324	189688321	1306064