Задача 1:

1. Составить программу и вычислить на ЭВМ интеграл заданной функции на отрезкес точностьюметодом Монте-Карло и методом Симпсона. Сравнить точность полученных результатов с точным значением интеграла.

2. Определить, какое число отрезков разбиения для метода Симпсона обеспечило бы достижение точности .

Решение:

Вариант		Подынтегральная функция f(x)		Пределы интегрирования
				a		b
	7				0	1

1. _{Вычислим точное значение интеграла:}

₀.5309799

Программа вычисления на ЭВМ интеграла заданной функции на отрезке с точностью методом Монте-Карло.

function y=monte(a, b, N, func)

S=0;

for i=1:N

S=S+func(rand() * (b-a)+a);

end

y=S*(b-a)/N

endfunction

function y=myf(x),y=x*sqrt(x*x+1) endfunction

printf('Интеграл по методу Монте-Карло = %.8f ',monte(0,1,100000,myf));

Интеграл по методу Монте-Карло = 0.5224005

Погрешность: = 0,000008317911

Метод симпсона:

function y=simpson(a, b, N, func)

S1=0;

S2=0;

for i=1:+2:N-1

S1=S1+func(a+i*(b-a)/N)

end

for i=2:+2:N-2

S2=S2+func(a+i*(b-a)/N)

end

h=(b-a)/N

y=h/3*(func(a)+func(b)+4*S1+2*S2)

endfunction

printf('%.8f',simpson(0,1,100,myf))

0.5309805

Погрешность: 0.0000000006

2. Определить, какое число отрезков разбиения для метода Симпсона обеспечило бы достижение точности .

Погрешность метода Симпсона вычисляется по формуле:

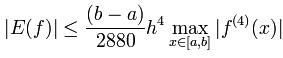
Для получаения максимального значения 4й переменной найдём её точки экстремума на промежутке [a,b]

при

Тогда

=max(|0.8264|,|0.553|,|-0.9646|)=0.553

Отсюда:

_{Точность будет достигаться приN=26 отрезках.}

Проверим: printf('%.8f',simpson(0,1,26,myf))

0.05311069

_{Погрешность:} 0.0000001269 <

Задача 2:

1. Построить графики функций.

2. Найти площадь фигуры, ограниченной этими графиками (с точностью ) методом Монте-Карло. Расчет точек пересечения заданных функций и расчет интегралов оформить отдельными программами.

Вариант	Заданные функции
7

Решение:

1. Построить графики функций.

function y=y1(x),y=exp(-2*x)endfunction

function y=y2(x),y=-sqrt(9-x^2)endfunction

function y=y3(x),y=0.1*x^2endfunction

function y=y4(x),x=0.8endfunction

x=[0:0.01:1]

plot(x,y1(x))

plot(x,y2(x))

plot(x,y3(x))

y4 =[0,3]

x = [0.8, 0.8];

plot(x, y4)

2. Найдём точки пересечения:

function z=f1(x, y),z=exp(-2*x)-y endfunction

function z=f2(x, y),z=y-exp(x) endfunction

function z=f3(x, y),z=y-0.1*x^2 endfunction

function z=f4(x, y),z=0.8-x endfunction

function [y]=intersect1(x)

y(1)=f1(x(1),x(2))

y(2)=f2(x(1),x(2))

endfunction

function [y]=intersect2(x)

y(1)=f1(x(1),x(2))

y(2)=f4(x(1),x(2))

endfunction

function [y]=intersect3(x)

y(1)=f2(x(1),x(2))

y(2)=f4(x(1),x(2))

endfunction

function [y]=intersect4(x)

y(1)=f2(x(1),x(2))

y(2)=f3(x(1),x(2))

endfunction

fsolve([-1,1],intersect1)

ans =

0

fsolve([0.5,1],intersect2)

ans =

0.8

fsolve([0.1,2],intersect3)

ans =

0.8

fsolve([0.4,0.7],intersect4)

ans =

0.576

Min(x) = 0 Max(x) = 0.8 Min(y) = 0.23 Max(y)= 2.23

Программа для нахождения площади методом Монте-карло:

function Sq=monte2d(funcs, N, xt, rect)

for i= 1:length(funcs)

z(i)=sign(funcs(i)(xt(1),xt(2)))

end

S=0

for j= 1:N

t(1)=rand(1,1,'uniform') * (rect(3)-rect(1))+rect(1)

t(2)=rand(1,1,'uniform') * (rect(4)-rect(2))+rect(2)

flag=1

for i= 1:length(funcs)

if~(sign(funcs(i)(t(1),t(2)))==z(i)) then

flag=0

end

end

S=S+flag

end

Sq=S*(rect(3)-rect(1))*(rect(4)-rect(2))/N

endfunction

Вкачестве точки принадлежащей области возьмём [2.5,0]

monte2d(list(f1,f2,f3,f4),100000000,[2.5,0],[0.0498,-1.0353,3,2.9996])

ans =

2.458764

Для оценки точности в качестве реальной площади возьмём площадь, вычесленную методом симпсона:

t=fsolve([0.1,3],intersect1)

g(1)=t(1)

t=fsolve([3,-1],intersect1)

g(2)=t(1)

t=fsolve([0.1,2],intersect2)

g(3)=t(1)

t=fsolve([2,-1],intersect2)

g(4)=t(1)

printf('%.7f',simpson(g(1),3,100000,y21)-simpson(g(1),g(3),100000,y1)-simpson(g(3),2,100000,y31)-(simpson(g(2),3,100000,y22)+simpson(g(4),g(2),100000,y1)-simpson(g(4),2,100000,y32)))

4.7070644

Погрешность: