8. Конечные разности различных порядков. Таблицы разностей.

Конечные разности различных порядков

y=f(x) обозначим ,h- фиксированная величина приращения аргумента функции или шаг.

Найдем приращение функции

1. Называется 1-й конечной разностью, n-я конечная разность вычисляется по формуле:

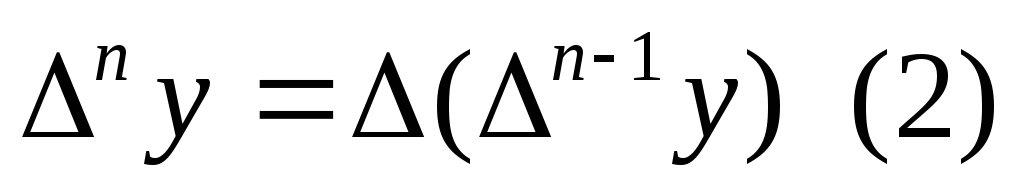
Пусть y=x³ x=1

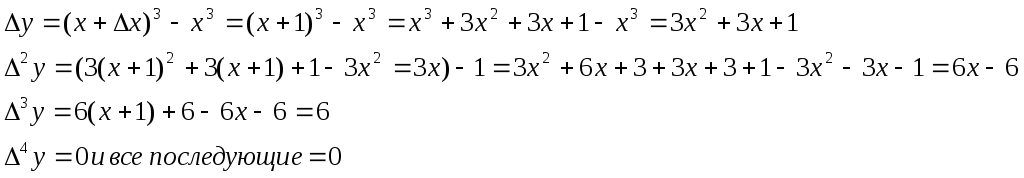
Пусть f(х)есть многочлен n-й степени

Свойства конечных разностей:

1. Конечная разность

2. 

3. 

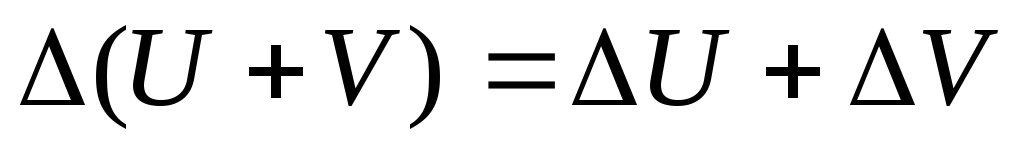
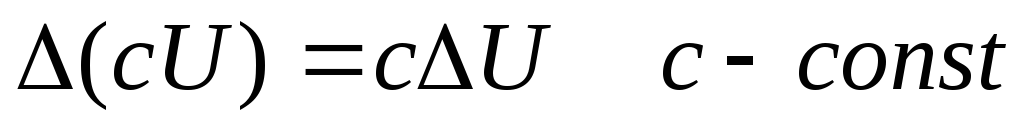
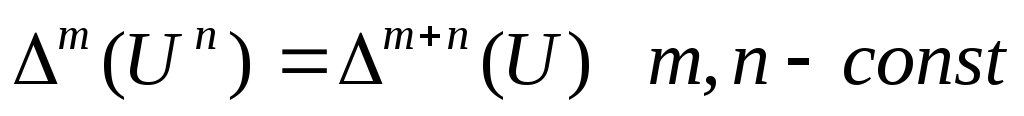
Выразим конечные разности через функции

Пусть функция y=f(x) имеет n-ю производную на отрезке , тогда можно записать, чтоn-я производная функции

Таблица конечных разностей

Приходится рассматривать функция заданную таблично где

Конечные разности последовательности y_i определяется соотношением

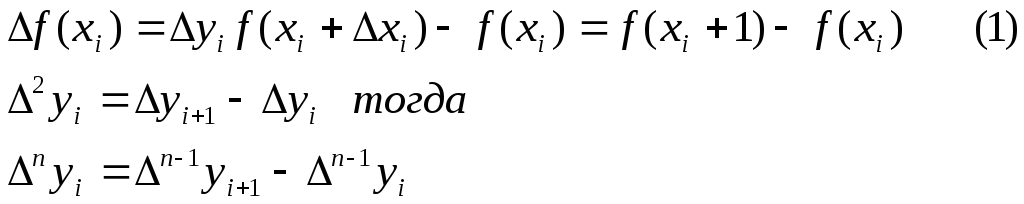
Вспомним бином Ньютона, можно показать что n-я конечная разность y_i может быть представлена как сумма

Данные конечные разности удобно располагать виде таблиц:

1. Горизонтальная

2. Диагональная

Чаще на практике используется горизонтальная таблица она имеет вид:

x	y	y	2y	3y
x0	y0	y0	2 y0	3 y0
x1	y1	y1	2y1	3y1
x2	y2	y2	2 y2	3 y2
…	…	..	…	…
xn	yn	yn	2 yn	3 yn

Диагональная

x	y	y	2y	3y
x0	y0	y0
x1	y1		2 y0
x2		y1	2y1	3 y0

8. Постановка задач аппроксимации функции, общей задачи интерполирования, простейшей задачи интерполирования.

Обобщенная степень

Обобщенной n степенью числа х называется произведение n сомножителей первой из которых является х, а каждый следующий сомножитель , на h меньше предыдущего.

Х^[n]- обозначение.

Найдем конечную разность для обобщенной степени.

f(x)=x^[n], тогда

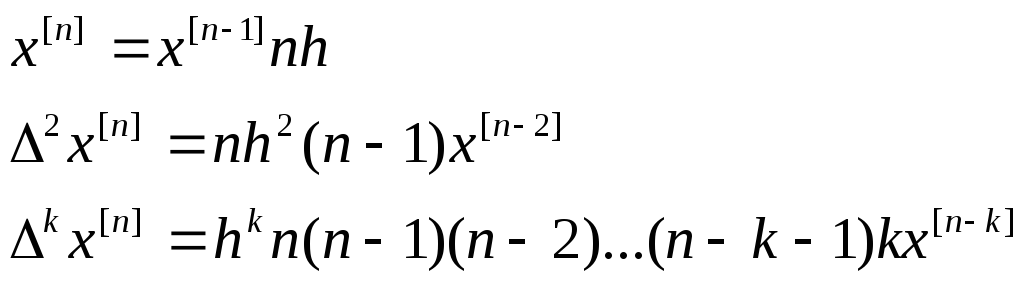
Постановка задачи интерполирования

Простейшие задачи интерполирования заключаются в следующем:

Пусть на отрезке [a,b] задана n+1 точка x₀,x₁,x₂….x_n.

Эти точки называются узлами интерполирования, для этих узлов интерполирования известно значение некоторых функций y=f(x)

Требуется построить функцию y=F(x) такую что F(x₀)=y₀, F(x₁)=y₁, F(x₂)=y₂….F(x_n)=y_n

Функция F(x) называется интерполирующей .

Аналитическое выражение f(x) очень сложное или неизвестное.

Геометрически это означает, что надо найти y=F(x) с некоторыми дополнительными свойствами в частности F(x) проходит через точку (x_i,y_i), y_i=f(x_i) i=1,n

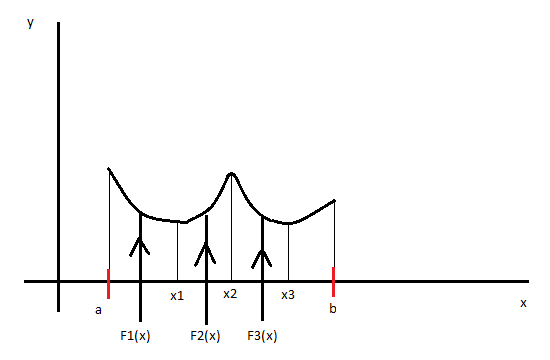
Задача в такой постановке может иметь бесконечное множество решений.

Задача становится однозначно решаемой, если в качестве функции y=f(x) рассматривать полином y=P_n(x) степени не выше n, которая удовлетворяет условию P_n(x_i)=y_i i=0,n.

n- количество точек. Полученная интерполирующая функция часто используется для приближенного вычисления значений функции y=f(x) в точках не совпадающих с узлами интерполяции

Такая операция называется интерполированием функции f(x).

Различают интерполирование в узком смысле и в широком. Данная операция носит название экстраполированием.

8. Первая интерполяционная формула Ньютона (общая формула и формулы для линейного и квадратичного интерполирования).

Пусть y=f(x) задана своими точками y_i=f(x_i) i=0,n, причем x_i=x₀+ih. h - шаг интерполирования.

Рассмотрим многочлен степени y=P_n(x) обладающий условием P_n(x_i)=y_i (1)

Условие (1) равносильно равенству:

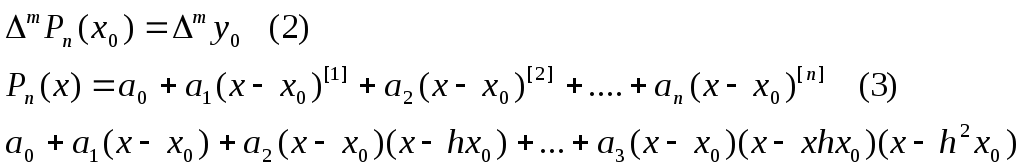
Полагая в равенстве (3) x=x₀ получим, что P_n(x₀)=a₀ следовательно a₀=y₀.

Вычисляя 1-ю конечную разность полинома P_n(x) (см (2)) и полагая, что x=x₀ мы получаем, что

Находя вторую конечную разность и пологая что x=x₀ , продолжая процесс мы получим, чтоi=0,n.

Подставляя в равенство (3) зная коэффициент a_i, получим:

- первый полином Ньютона.

Обычно первый полином Ньютона записывается в более удобном виде:

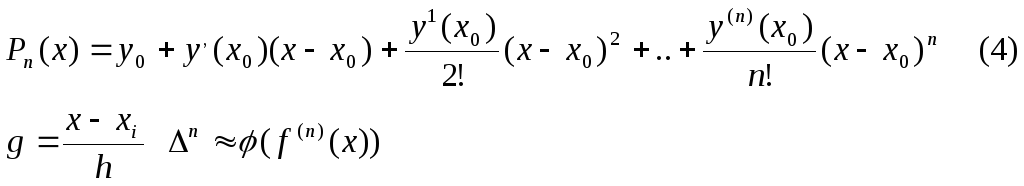
Формула (4) неудобная для практического применения. Поэтому был введен второй интерполяционный полином Ньютона: