Геометрическая интерпретация
Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка и берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.
Пусть
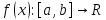— определённая на отрезке
и дифференцируемая на нём вещественнозначная
функция. Тогда формула итеративного
исчисления приближений может быть
выведена следующим образом:
где
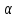— угол наклона касательной в точкеxn.
Следовательно искомое выражение для xn+1 имеет вид:
Итерационный процесс начинается с некоего начального приближения (чем ближе к нулю, тем лучше, но если предположения о нахождении решения отсутствуют, методом проб и ошибок можно сузить область возможных значений, применив теорему о промежуточных значениях).
Алгоритм
Задается начальное приближение x0.
Пока не выполнено
условие остановки, в качестве которого
можно взять
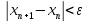или
(то есть погрешность в нужных пределах),
вычисляют новое приближение:
.
Задача: Методом Ньютона вычислить минимум функции двух переменных.
Алгоритм: Пусть (x0, y0) – начальное приближение для точки минимума. Очередное приближение вычисляется по формуле:
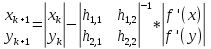
где ƒ’(x), ƒ’(y) – производные функции ƒ(x, y) по x и по y, а hi, j - элементы матрицы Гессе (матрицы вторых производных):
h1,1 = ƒxx h1,2 = h2,1 = ƒxy h2,2 = ƒyy
В покомпонентном виде приведенная выше формула имеет вид:
xk+1 = xk - (h2,2 * ƒ’(xk)- h1,2 * ƒ’(yk)) / det(h)
yk+1 = yk - (- h2,1 * ƒ’(xk) + h1,1 * ƒ’(yk)) / det(h)
где det(h) - определитель матрицы h.
Счёт ведется итерациями до тех пор, пока два последовательных приближения не будут отличаться по третьей норме больше, чем на ε.
Контрольный пример
Начальная точка
(4, -1, 2).
Рис. 2. – График функции
|
X |
y |
z |
h33 * dx |
h22 * dy |
h11 * dz |
det(h) |
|
4 |
-1 |
2 |
48 |
-16 |
112 |
32 |
|
2,5 |
-0,5 |
-1,5 |
24 |
-14 |
56 | |
|
1,75 |
-0,0625 |
-3,25 |
12 |
-12,25 |
28 | |
|
1,375 |
0,320313 |
-4,125 |
6 |
-10,7188 |
14 | |
|
1,1875 |
0,655273 |
-4,5625 |
3 |
-9,37891 |
7 | |
|
1,09375 |
0,948364 |
-4,78125 |
1,5 |
-8,20654 |
3,5 | |
|
1,046875 |
1,204819 |
-4,89063 |
0,75 |
-7,18073 |
1,75 | |
|
1,023438 |
1,429216 |
-4,94531 |
0,375 |
-6,28313 |
0,875 | |
|
1,011719 |
1,625564 |
-4,97266 |
0,1875 |
-5,49774 |
0,4375 | |
|
1,005859 |
1,797369 |
-4,98633 |
0,09375 |
-4,81052 |
0,21875 | |
|
1,00293 |
1,947698 |
-4,99316 |
0,046875 |
-4,20921 |
0,109375 | |
|
1,001465 |
2,079235 |
-4,99658 |
0,023438 |
-3,68306 |
0,054688 | |
|
1,000732 |
2,194331 |
-4,99829 |
0,011719 |
-3,22268 |
0,027344 | |
|
1,000366 |
2,29504 |
-4,99915 |
0,005859 |
-2,81984 |
0,013672 | |
|
1,000183 |
2,38316 |
-4,99957 |
0,00293 |
-2,46736 |
0,006836 | |
|
1,000092 |
2,460265 |
-4,99979 |
0,001465 |
-2,15894 |
0,003418 | |
|
1,000046 |
2,527732 |
-4,99989 |
0,000732 |
-1,88907 |
0,001709 | |
|
1,000023 |
2,586765 |
-4,99995 |
0,000366 |
-1,65294 |
0,000854 | |
|
1,000011 |
2,63842 |
-4,99997 |
0,000183 |
-1,44632 |
0,000427 | |
|
1,000006 |
2,683617 |
-4,99999 |
9,16E-05 |
-1,26553 |
0,000214 | |
|
1,000003 |
2,723165 |
-4,99999 |
4,58E-05 |
-1,10734 |
0,000107 | |
|
1,000001 |
2,757769 |
-5 |
2,29E-05 |
-0,96892 |
5,34E-05 | |
|
1,000001 |
2,788048 |
-5 |
1,14E-05 |
-0,84781 |
2,67E-05 | |
Табл. 1. – Значения x, y и z, а также числителей и детерминанта для вычисления этих значений
Рис. 3. – График сходимости при начальной точке (4, -1, 2)
Рис. 4. – График сходимости при начальной точке (0, 2, -4)
Рис. 5. – График сходимости при точности 0.1
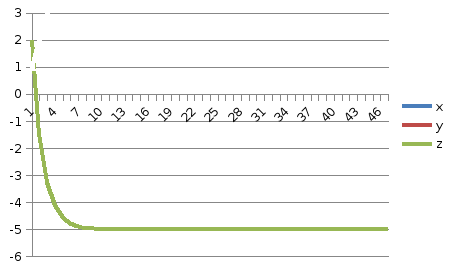
Рис. 6. – График сходимости при точности 0.01
Функция
для исследования:
Рис. 7. – График функции
|
x |
Y |
h11 |
h12 |
h22 |
f(x,y)dx |
f(x,y)dy |
det(h) |
|
5 |
-1 |
30,45623 |
-12,1825 |
24,36499 |
48,72998 |
-24,365 |
593,6526 |
|
3,5 |
-0,75 |
11,59912 |
-4,31595 |
11,50921 |
17,44364 |
-8,6319 |
114,8692 |
|
2,076577 |
-0,53378 |
4,491822 |
-1,50761 |
5,648757 |
6,159265 |
-3,01521 |
23,10033 |
|
0,767226 |
-0,34946 |
1,793873 |
-0,51285 |
2,935155 |
2,120168 |
-1,0257 |
5,002276 |
|
-0,37165 |
-0,19899 |
0,761482 |
-0,16525 |
1,660835 |
0,692546 |
-0,3305 |
1,237389 |
|
-1,25706 |
-0,08809 |
0,366789 |
-0,04699 |
1,066751 |
0,200203 |
-0,09398 |
0,389065 |
|
-1,79463 |
-0,02368 |
0,224818 |
-0,00965 |
0,815325 |
0,041975 |
-0,01931 |
0,183207 |
|
-1,98041 |
-0,0022 |
0,187569 |
-0,00082 |
0,742999 |
0,003639 |
-0,00163 |
0,139363 |
|
-1,99981 |
-2,1E-05 |
0,183976 |
-7,8E-06 |
0,735831 |
3,58E-05 |
-1,6E-05 |
0,135375 |
|
-2 |
-2,1E-09 |
0,18394 |
-7,6E-10 |
0,735759 |
3,57E-09 |
-1,5E-09 |
0,135335 |
|
-2 |
-2E-17 |
0,18394 |
-7,4E-18 |
0,735759 |
0 |
-1,5E-17 |
0,135335 |
|
-2 |
0 |
0,18394 |
0 |
0,735759 |
0 |
0 |
0,135335 |
Табл. 2. – Значения x, y и z, а также производных и детерминанта для вычисления этих значений