Методы поиска глобального экстремума функции нескольких переменных. Условия Куна-Таккера. Условие Слейтера.

Метод множителей Лагранжа можно использовать при построении критериев оптимальности для задач с ограничениями в виде равенств. Кун и Таккер обобщили этот подход на случай общей задачи нелинейного программирования с ограничениями, как в виде равенств, так и в виде неравенств. Рассмотрим следующую общую задачу нелинейного программирования:

Минимизировать f(x) при ограничениях:

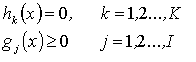
, где x = x₁, x₂, x₃,…, x_n.

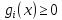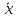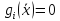Ограничения в виде неравенства называется активным, или связывающим, в точке, если, и неактивным, или не связывающим, если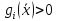, где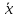- допустимая точка, то есть удовлетворяющая всем ограничениям. Если существует возможность обнаружить ограничения, которые неактивны в точке оптимума, до непосредственного решения задачи, то эти ограничения можно исключить из модели и тем самым уменьшить ее размеры.

Кун и Таккер построили необходимые и достаточные условия оптимальности для задач нелинейного программирования, исходя из предположения о дифференцируемости функций f, g_j, h_k. Итак, задача Куна - Таккера состоит в том, чтобы найти векторы 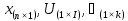, удовлетворяющие следующим условиям:

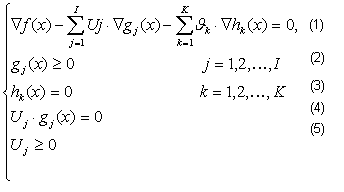
Прежде всего, проиллюстрируем условия Куна-Таккера на примере.

Минимизировать 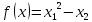при ограничениях:

Записав данную задачу в виде задачи линейного программирования, можно получить:

Уравнение (1), входящее в состав условий Куна-Таккера принимает следующий вид:

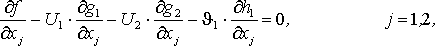
откуда

Неравенства (2) и уравнения (3) задачи Куна-Таккера в данном случае записывается в виде:

Уравнения (4), известные как условие дополняющей нежесткости, принимают вид:

Заметим, что на переменные U1 и U2 накладывается требование неотрицательности, тогда как ограничение на знак, отсутствует. Таким образом, для данной задачи условия Куна-Таккера записываются в следующем виде:

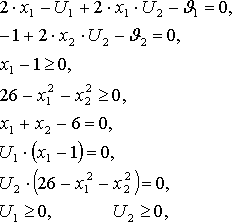
Условие регулярности Слейтера

Необходимое условие экстремума в задаче нелинейного программирования, оказывается верным только при выполнении дополнительных условий, которым должна удовлетворять задача:

Важнейшим из них является так называемое условие регулярности Слейтера:

Говорят, что функция g_i(х), задающая ограничение в задаче, удовлетворяет условию регулярности Слейтера, если существует такая точка 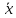, принадлежащая области допустимых планов D, что

,

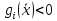т. е. является внутренней точкой относительно ограничения g_i(x). Поэтому данное условие также называют условием телесности.

Вообще говоря, существуют разные варианты необходимого условия Куна—Таккера. Приведем один из них.

Если (D, f) является задачей выпуклого программирования с решением х, ее целевая функция f(x) и функции ограничений g_i(x) — дифференцируемы, нелинейные ограничения в форме неравенств удовлетворяют условию регулярности Слейтера, то существует такой вектор u ≥ 0, что (х,u) — седловая точка функции Лагранжа Ф(х,u).

Значение теоремы Куна—Таккера состоит в том, что она позволяет связать процесс решения оптимизационной задачи с поиском седловых точек функции Лагранжа, т. е., грубо говоря, с максимизацией этой функции по х и минимизацией по u.

Определим F(x) как функцию, ставящую в соответствие каждому значению х минимальное значение функции Ф(х,u) по u:

и по аналогии

Рассмотрим задачу отыскания максимума функции F(x)

и задачу минимизации G(u)

Очевидно, что

Отсюда следует, что максимум F(x) находится в допустимой области D и совпадает с максимумом целевой функции f(x) задачи (1):

Таким образом, задача (2), в определенном смысле, равносильна (1). Аналогичные выводы могут быть получены и для (3). Задачи (2) и (3) образуют двойственную пару. Как нетрудно догадаться, данное отношение является обобщением отношения двойственности для задач линейного программирования. Соответственно, при определенных условиях пара двойственных задач нелинейного программирования обладает свойствами, аналогичными свойствам двойственных линейных задач. В частности, при любых х∊Х, u ≥ 0.

Условие (4) находит широкое применение при построении оценок в итеративных методах решения оптимизационных задач. Например, если имеется возможность приблизительно решить прямую и двойственную задачи и получить последовательности приближений {х^(q)} и {u^(q)}, то с помощью неравенств вида

можно определить момент остановки вычислительной процедуры.

В заключение отметим, что возможен вариант вывода выражений для целевых функций и ограничений пары двойственных задач линейного программирования из общего определения отношения двойственности для нелинейных задач. Также отметим, что в процессе формирования нелинейных двойственных задач существует большая неоднозначность: их вид можно варьировать, включая в множество Х часть ограничений g_i(x) ≤ 0.