Оглавление

Теоретическая часть 4

Теория математического программирования. Однокритериальная оптимизация. Необходимые и достаточные условия для локальных экстремумов гладких функций 4

Методы поиска глобального экстремума функции нескольких переменных. Условия Куна-Таккера. Условие Слейтера. 7

Линейное программирование. Угловые точки допустимых множеств. 12

Нелинейное программирование. Постановка общей задачи нелинейного программирования 20

Практическая часть 22

Метод Ньютона 22

Список литературы 29

Теоретическая часть Теория математического программирования. Однокритериальная оптимизация. Необходимые и достаточные условия для локальных экстремумов гладких функций

Условия экстремума являются основой, на которой строят методы решения задач оптимизации. Они определяют информацию о свойствах решения. В этом разделе будут рассмотрены условия экстремума задачи минимизации без ограничений:

.

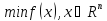1. Понятия локального и глобального экстремумов. Точка называется точкой локального минимума функции f(x), если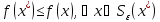, где- окрестность точки.

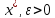Точка 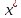называется точкой глобального минимума функции f(x), если.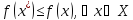

Точка х называется стационарной, если в ней выполнено условие

. (1.1)

Теорема 1.1. (Необходимое условие 1 порядка). Пусть - точка минимума f(x),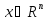, и f(x) дифференцируема в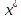, тогда выполняется условие стационарности (1.1).

Доказательство следует из возможности линейного представления функции в точке .

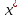Не всякая из точек, удовлетворяющих (1.1), является точкой минимума.

Теорема 1.2. (Достаточное условие 1-го порядка). Пусть f(x) - выпуклая функция, дифференцируемая в точке , и выполнено условие (1.1). Тогда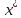- точка глобального минимума f (x) на .

Доказательство следует из

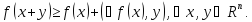
Теорема 1.3. (Необходимое условие 2-го порядка). Пусть -точка минимума f(x),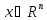и f(x) дважды дифференцируется в.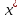

Тогда .

Теорема 1.4. (Достаточное условие 2-го порядка). Пусть в точке 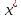функция f(x) дважды дифференцируема, выполнено условие (1.1) и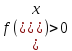. Тогда точка- точка локального минимума.

Теорема 1.5. (Существование решения). Пусть f(x) непрерывна на 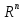и множестводля некоторого A не пусто и ограниченно. Тогда существует точка глобального минимума на.

Теорема 1.6. Точка минимума строго выпуклой функции, если она существует, единственна.

Теорема 1.7. Точка минимума сильно выпуклой функции существует и единственна.

Основные теоремы дифференциального исчисления: Теорема Ферма (необходимое условие экстремума для гладких функций)

Пусть f(x) функция, заданная на закрытом интервале [ a, b ], дифференцируемая на открытом (a, b) такая что в точке С выполнено: является точкой экстремума, т.е. точкой максимума или минимума. Тогда в точке С производная равна нулю.

Док-во: Пусть С — точка максимума, т.е. аналогично С точка минимума, т.е., тогда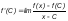. Оценимпри х > С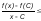 и0 при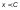. Тогда, переходя к пределу, при х→С получим, а это возможно только еслиf''(C) = 0. Замечание: Теорему Ферма можно рассматривать как теорему о необходимых условиях экстремума функции на открытом интервале.