
АГ ПЗ 1-35 (полный вариант)
.pdf
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 9, с.17
ной плоскости Оху. Тогда расстояние между ними можно вычислить по формуле:
AB (xB xA )2 (yB yA )2 .
Теорема. (О модуле вектора.) Модуль вектора равен корню квадратному из суммы квадратов его координат:
| a | a2x a2y .
Обозначим углы между вектором и координатными осями: (a ^ Ox) , (a ^ Oy) .
у
a
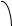 х
х
Рис. 7
Определение. Углы между вектором и координатными осями называются его направляющими углами, а их косинусы – его направляющими косинусами.
Теорема. (О направляющих косинусах вектора.) Пусть a (ax ; ay ) . Тогда
cos |
a |
x |
, cos |
ay |
и cos2 |
cos2 1. |
|||||
|
|
|
|
|
|
|
|||||
| a | |
| a | |
||||||||||
|
|
|
|
||||||||
Определение. Вектор единичной длины, сонаправленный с вектором a называется его ортом, и обозначается ao .
Теорема. (Об орте вектора.) Направляющие косинусы вектора являются координатами его орта:
5
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 9, с.17
ao | aa | (cos ; cos ) .
п.1.6. Деление отрезка в данном отношении |
|
||
Теорема. (О координатах |
точки, |
делящей отрезок.) |
Пусть |
A(xA , yA ), B(xB , yB ), C(xC , yC ) |
– три |
произвольные точки |
коорди- |
натной плоскости Оху, лежащие на одной прямой L, и точка С делит отрезок АВ в отношении CAB , считая от точки А. Тогда
xC |
xA xB |
, yC |
yA yB |
и CAB |
xC xA |
|
yC yA |
. |
||||
1 |
1 |
xB xC |
|
|||||||||
|
|
|
|
|
|
yB yC |
||||||
Следствие. Если точка С есть середина отрезка АВ, то |
|
|
|
|||||||||
|
|
xC |
xA xB |
, yC |
yA yB |
. |
|
|
|
|||
|
|
|
|
|
|
|
||||||
|
|
2 |
|
2 |
|
|
|
|
|
|||
п.2. Список задач Список №1
1.Построить чертеж общей ДСК на плоскости с данным координатным углом, и отметить на нем точку с заданными координатами.
2.Найти расстояние от данной точки плоскости до координатных осей
в общей ДСК с данным координатным углом.
Следующие задачи предполагается решать в ПДСК на плоскости.
3.Построить чертеж ПДСК на плоскости, и отметить на нем точку с заданными координатами.
4.Найти на координатной плоскости точку, симметричную данной относительно координатных осей и начала координат.
5.Построить в ПДСК на плоскости радиус-вектор точки с заданными координатами, и найти его координаты.
6.В ПДСК на плоскости отложить от данной точки вектор с данными координатами.
7.Дан вектор в координатной форме записи. Найти его модуль, орт и направляющие косинусы.
8.Дан орт вектора и его модуль. Найти его координаты, и записать в координатной форме. Построить чертеж координатной плоскости, и отложить от начала координат найденный вектор и его орт.
9.Дан модуль вектора и один из двух направляющих углов. Найти координаты вектора, и отложить его от начала координат.
6
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 9, с.17
10.Найти координаты вектора по известным координатам его начала
иконца.
11.Найти координаты суммы векторов и произведения вектора на число.
12.Найти расстояние между двумя точками с известными координатами.
13.Найти отношение, в котором данная точка делит данный отрезок.
14.На данном отрезке найти координаты точки, делящей данный отрезок в данном отношении.
15.Найти координаты середины отрезка.
Список №2
1.Зная расстояния от точки до координатных осей, найти её координаты в данной общей ДСК.
2.Найти на координатной плоскости точку симметричную данной относительно биссектрисы координатного угла, и биссектрисы угла, смежного с координатным.
3.Найти на координатных осях точку, удаленную от данной точки на данное расстояние.
4.Точка с одной известной координатой делит данный отрезок в данном отношении. Найти неизвестную координату этой точки.
п.3. Примеры Пример 1. Построить точку М(2; 1) в общей ДСК с координатным уг-
лом 60o , и найти расстояния от неё до координатных осей.
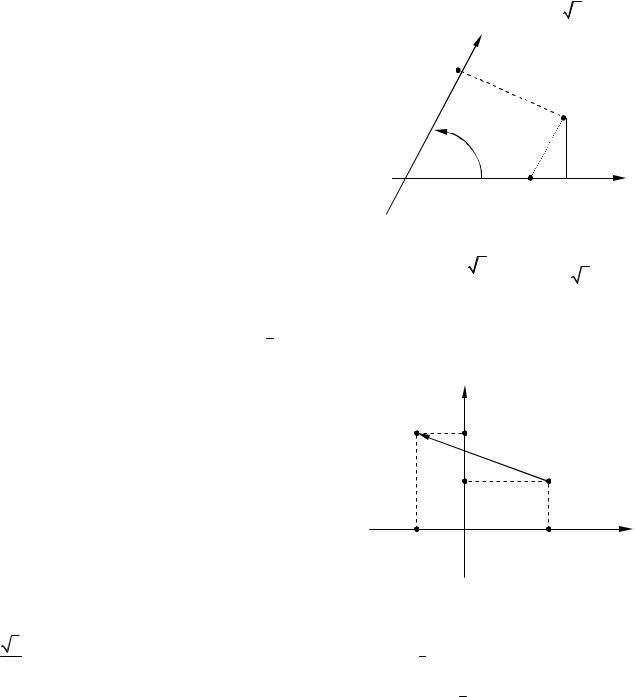
Решение. Смотрите рисунок 8. На оси Ох откладываем точку С(2). На оси Оу откладываем точку D(1). Через точки С и D проводим прямые, параллельные координатным осям. Их точка пересечения есть искомая точка М(2; 1). Из точки М опускаем перпендикуляры на координатные оси: МА и МВ. Это искомые расстояния от точки М до координатных осей. По построению, OCMD является параллелограммом, поэтому CM OD 1, MD OC 2 . В прямоугольном треугольнике
АМС, угол А прямой, угол АСМ равен координатному углу, следовательно,
AM CM sin 60o 23 .
Аналогично, из треугольника DMB находим
7
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 9, с.17
BM DM sin 60o 3 .
у
В
М
D(1) 
60o
х
ОС(2) А
|
|
Рис. 8 |
|
Ответ: рисунок 8, d(M,Ox) |
3 |
, d(M,Oy) 3 . |
|
2 |
|||
|
|
Пример 2. Отложить на координатной плоскости Оху вектор a ( 3;1) от точки А(2; 1).
Решение. Смотрите рисунок 9.
у
B F(2)
А(2;1)
D(1)
х
E(–1) O С(2)
Рис. 9
Обозначим через В – конец искомого вектора, С и D – проекции точки А на координатные оси.
Проекция вектора a на ось абсцисс равна минус 3, поэтому откладываем на оси Ох от точки С влево от нее 3 единицы и отмечаем точ-
ку Е(–1). Проекция вектора a на ось равна 1, поэтому откладываем на
8
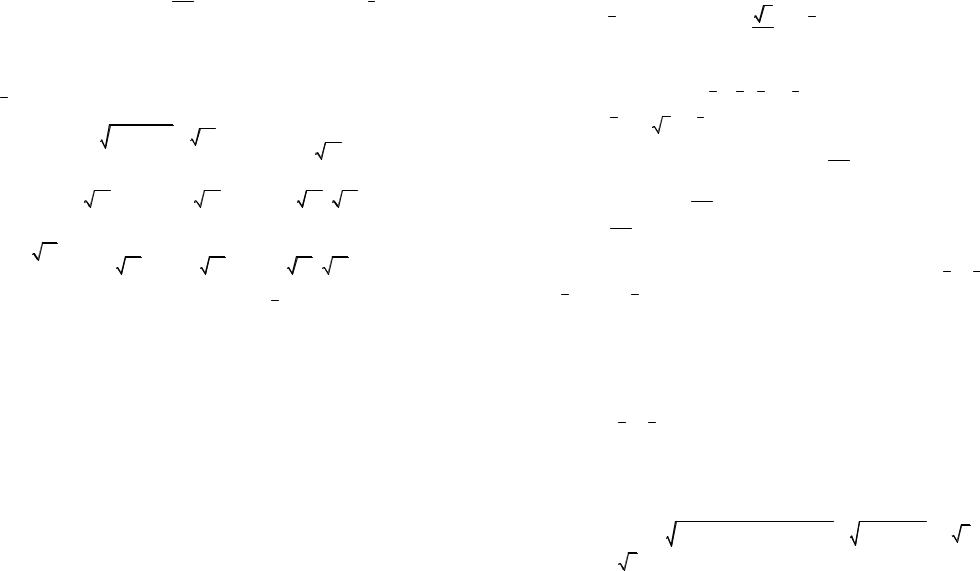
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 9, с.17
оси Оу от точки D вверх от нее одну единицу и отмечаем точку F(2). В точках Е и F восстанавливаем перпендикуляры. Их точка пересечения есть искомая точка В.
Построенный вектор AB равен данному вектору a , так как равны их координаты – их проекции на координатные оси.
Ответ: рисунок 9.
Пример 3. Найти модуль, орт и направляющие косинусы вектора a ( 3;1) .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
10 , cos |
|
ax |
|
|
3 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Решение. |
| a | |
( 3) |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
||||||||||||||||||||||
|
|
| |
|
| |
|
10 |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
a |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
ay |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
1 |
|
|
||||||
cos |
|
|
|
|
o |
|
a |
|
|
( 3;1) |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
, a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Ответ: |
| a | |
|
|
10 |
|
|
|
|
|
|
|
| a | |
|
|
10 |
|
|
|
|
|
|
|
|
|
10 |
|
|
10 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
1 |
|
|
|
o |
|
|
|
3 |
|
1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
| a | 10, cos |
|
|
|
|
|
|
, cos |
|
|
, a |
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
. |
|||||||||||||||||
10 |
|
10 |
|
10 |
10 |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Пример 4. Найти координаты вектора a , и записать его в координатной форме, если его модуль равен 10, а его направляющий угол в 2
раза больше направляющего угла . Решение. Воспользуемся соотношением
cos2 cos2 1,
и тем, что по условию задачи 2 . Получаем уравнение
cos2 cos2 2 1 .
Воспользуемся формулой косинуса половинного аргумента:
cos2 1 cos2 , 2
и, подставляя в уравнение, получаем
2cos2 2 cos 2 1 0 .
Решая последнее уравнение находим его корни, учитывая, что, по определению, направляющий угол не превосходит 180o :
1 6 ; 2 2 .
9
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 9, с.17
Следовательно, 1 3 ; 2 . Теперь, зная направляющие углы век-
тора, находим его орт:
a1o (cos 1;cos 1) ( 23 ; 12), ao2 (cos 2 ;cos 2 ) (0; 1) .
Умножая орт вектора на его модуль, получаем запись вектора в координатной форме:
a | a | ao | a | (cos ; cos ) . Ответ: a1 (5 3;5), a2 (0; 10) .
Пример 5. Найти координаты вектора AB , если А(1; 3), В(–1; 7). Решение. Воспользуемся формулой:
AB (xB xA ; yB yA ) ( 2;4) . Ответ: AB ( 2;4) .
Пример 6. Найти координаты вектора 2a 4b , если a (5; 1), b (2;7) .
Решение. Действия с векторами в координатной форме удобнее производить, когда координаты вектора записаны не в строчку, а столбцом:
|
|
|
|
|
|
5 |
|
|
2 |
|
10 |
|
|
8 |
|
2 |
|
|||
2a 4b 2 |
4 |
|||||||||||||||||||
|
|
|
|
2 |
|
|
28 |
|
|
30 |
. |
|||||||||
|
|
|
|
|
|
1 |
|
|
7 |
|
|
|
|
|
|
|
||||
Ответ: 2a 4b (2; 30) .
Пример 7. Найти расстояние между точками: А(1; 3), В(–1; 7). Решение. Воспользуемся формулой расстояния между двумя точками координатной плоскости:
AB (xB xA )2 (yB yA )2 ( 2)2 42 2 5 .
Ответ: 2 5 .
Пример 8. Найти отношение, в котором точка С(2; 1) делит отрезок А(1; 3), В(–1; 7), считая от точки А.
Решение. 1-й способ. Сначала убеждаемся в том, что данные точки
10
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 9, с.17
находятся |
на |
одной прямой. |
|
Находим координаты векторов |
|||||
|
|
( 3;6) |
и |
|
(1; 2) . Координаты этих векторов пропорцио- |
||||
|
CB |
AC |
|||||||
нальны: |
|
|
1 |
|
|
2 , |
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
3 |
|||
|
|
|
|
|
|
|
6 |
||
следовательно, векторы коллинеарные и данные точки лежат на одной прямой. Более того,
AC (1; 2) 13 CB 13 ( 3;6) .
Из определения отношения, в котором точка С делит отрезок АВ, считая от точки А:
AC CAB CB ,
находим, что CAB 13 .
2-й способ. Если данные точки находятся на одной прямой, то верны равенства:
CAB xC xA yC yA . |
|
xB xC |
yB yC |
Подставляя данные координаты в эти равенства, получаем:
2 1 |
|
1 3 |
|
|
1 . |
|
1 2 |
7 1 |
|||||
|
|
3 |
||||
Следовательно, данные точки лежат на одной прямой и искомое отношение CAB 13 .
3-й способ. Сначала убедимся в том, что данные точки лежат на одной прямой. Для этого найдем длины отрезков АВ, АС, СВ:
AB 2 5, AC 5, CB 3 5 .
Так как CB CA AB , то это означает, что точки А, В и С лежат на одной прямой. Далее, воспользуемся теоремой о вычислении отношения, в котором точка С делит отрезок АВ, считая от точки А:
CAB ACCB ,
где знак плюс берется в том случае, когда точка С делит отрезок АВ внутренним образом, и знак минус, когда точка С делит отрезок АВ
11
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 9, с.17
внешним образом. Получаем отсюда: CAB ACCB 3 55 13 . Если
бы точка С находилась между точками А и В на отрезке АВ, тогда выполнялось бы одно из следующих неравенств:
xA xC xB или xB xC xA ,
но в нашем случае, xC 2 xA 1 xB 1. Это означает, что точка С делит отрезок АВ внешним образом, и нужно выбрать знак минус. Ответ: CAB 13 .
Пример 9. Найти координаты точки С, если известно, что она делит отрезок А(1; 3), В(–1; 7), считая от точки А, в отношении 3 : 2. Решение. Воспользуемся формулами:
|
x |
A |
C |
x |
B |
|
y |
A |
C y |
B |
|
xC |
|
AB |
|
, yC |
|
AB |
. |
||||
|
|
1 CAB |
|
|
|
1 CAB |
|
||||
|
|
|
|
|
|
|
|
|
|||
По условию задачи, CAB 32 . Из данных формул находим:
|
|
|
|
1 |
3 |
( 1) |
|
1 |
|
3 |
3 |
7 |
|
27 |
|
2 . |
||||||
|
|
xC |
|
2 |
|
, yC |
2 |
|
5 |
|||||||||||||
|
|
|
|
|
|
3 |
|
5 |
|
|
|
5 |
||||||||||
|
|
|
|
|
|
1 |
|
|
|
1 |
3 |
|
|
|
5 |
|||||||
|
|
1 |
|
2 |
|
2 |
|
|
|
|
2 |
|
|
|
|
|
||||||
|
|
; 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: C |
5 |
5 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 10. Найти координаты середины отрезка АВ, если А(1; 3),
В(–1; 7).
Решение. Воспользуемся формулами координат середины отрезка:
xC |
xA xB |
|
1 ( 1) |
0, yC |
yA yB |
|
3 7 |
5 . |
|
2 |
|
2 |
|||||
2 |
|
2 |
|
|
||||
Ответ: (0; 5).
п.3. Задачи Задачи для аудиторного решения 9
1.Построить точки с данными координатами в косоугольной системе координат с координатным углом 60o : А(1; 2); В(–3; 1); С(1; –2);
12

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 9, с.17
D(–2; –2).
2.Относительно косоугольной системы координат с координатным углом 45o дана точка М(4; 2). Определить расстояние от этой точ-
ки до осей координат.
Следующие задачи решаем в ПДСК.
3.Постройте на координатной плоскости точку А(1; 4) и точки, симметричные данной относительно координатных осей и начала координат.
4.Постройте на координатной плоскости точку А(1; 4) и её радиусвектор, и найдите его координаты.
5.Отложите от точки А(–2; –3) вектор a ( 1;7) .
6.Найдите модуль, направляющие косинусы и орт вектора a ( 1;7) .
7. Найдите координаты вектора |
|
, если | |
|
| 2 и |
|
o ( |
3 |
; |
4) . |
|
|
||||||||
a |
a |
a |
|||||||
|
|
|
|
|
|
|
5 |
|
5 |
8.Найдите координаты вектора, если его модуль равен 5, а угол между вектором и осью ординат равен 150o .
9. Найдите координаты вектора |
|
|
8 |
; |
9 |
|
|
|
7 |
; |
11 |
|
|||||||||
AB , если |
|||||||||||||||||||||
A |
4 |
|
, B |
4 |
3 |
. |
|||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||||
10. |
Найдите |
координаты |
|
вектора |
|
|
|
|
|
|
|
|
, |
если |
|||||||
|
d |
a |
2b |
3c |
|||||||||||||||||
a( 1; 7), b (2;5), c (1; 3) .
11.Даны две смежные вершины квадрата А(3; –7) и В(–1; 4). Вычислите его площадь.
12.Найдите отношение, в котором точка С(4; 5) делит отрезок АВ, считая от точки А, если А(1; –1), В(3; 3). Убедитесь сначала, что данные точки лежат на одной прямой.
13.На отрезке АВ, где А(–4; 5), В(1; –1), найдите точку С, которая делит его в отношении 3 : 5, считая от точки А.
14.Найдите координаты середины отрезка АВ, если:
|
8 |
; |
9 |
|
|
7 |
; |
11 |
|
а) А(–4; 5), В(1; –1); б) A |
3 |
|
, B |
4 |
3 |
. |
|||
|
|
4 |
|
|
|
|
Задачи повышенного уровня сложности 9
15. Определить координаты точки М в косоугольной системе координат с координатным углом 6 , если расстояние ее от осей координат равны соответственно 1 и 1,5.
13
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 9, с.17
16.Определить координаты вершин правильного шестиугольника со стороной 1, если за оси координат принять две его смежные стороны, так, что вершина противолежащая началу координат, имеет положительные координаты.
17.Через точку А(4; 2) проведена окружность, касающаяся координатных осей. Определить ее центр и радиус.
18.Даны три точки А(1; –1), В(3; р) и С(4; 5). При каком р треугольник АВС прямоугольный?
(ответ: |
|
11 |
; 2 |
|
2; |
2 |
11 ) |
||
|
|
|
|
19. Даны две смежные вершины квадрата А(2; –1) и В(–1; 3). Найти координаты двух его других вершин.
20.Прямая линия отсекает на оси Ох отрезок OA 4 и на оси Оу отрезок OB 7 . Найти координаты основания перпендикуляра, опущенного из начала координат на данную прямую.
21.Сторона ромба равна 5 2 , две его противоположные вершины имеют координаты (4; 9) и (–2; 1). Докажите, что этот ромб является квадратом.
22.В треугольнике с вершинами А(2; 3), В(6; 3) и С(6; –5) найти длину биссектрисы внутреннего угла В.
23.Покажите, что точки А(–3; 8), В(1; 5) и С(4; 1) могут служить тремя вершинами ромба ABCD (или ABDC).
а) Используя равенство AB CD , найдите координаты точки D. б) Вычислите площадь этого ромба.
Домашнее задание 9. ПДСК на плоскости
1.Найти координаты точки, симметричной точке А(–3; –5) относительно оси абсцисс косоугольной системы коорди-
нат с координатным углом 60o .
2.В треугольнике с вершинами А(2; 3), В(6; 3) и С(6; –5) найти: а) длину высоты ВD; б) отношение в котором точка D делит отрезок
АС и координаты точки D; в) координаты вектора BD и его направляющие углы; г) координаты, модуль, орт и направляющие углы вектора CM 34 BA .
14

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 9, с.17
Самостоятельная работа 9
Вариант 1.
1.Определение угла между векторами.
2.На координатной плоскости Оху даны точки А(–3; 2) и В(1; –1): а) постройте точки А и В на плоскости Оху;
б) найдите координаты вектора AB ;
в) найдите координаты середины отрезка АВ; г)* докажите, что начало координат не лежит на прямой, проходящей через точки А и В.
Вариант 2.
1.Определение угла между вектором и осью.
2.На координатной плоскости Оху даны точки А(–1; –1) и В(3; 2): а) постройте точки А и В на плоскости Оху;
б) найдите координаты вектора AB ;
в) найдите координаты середины отрезка АВ.
г)* докажите, что начало координат не лежит на прямой, проходящей через точки А и В.
Вариант 3.
1.Определение координат вектора в ПДСК на плоскости.
2.Отложите вектор AB (1; 2) от точки А(–2; 1), и: а) постройте чертеж и найдите координаты точки В;
б) найдите модуль вектора AB и его направляющие косинусы. Вариант 4.
1.Определение координат точки в ПДСК на плоскости.
2.Отложите вектор AB ( 1; 2) от точки А(2; –1), и:
а) постройте чертеж и найдите координаты точки В;
б) найдите модуль вектора AB и его направляющие косинусы.
п.5. Вопросы и задачи для самоконтроля 9 Обозначения
1.Обозначение угла между векторами, между вектором и осью.
2.Обозначение координат точки М на координатной плоскости Оху.
3.Обозначение координат вектора.
4.Координатная форма записи вектора.
5.Обозначение направляющих углов вектора.
6.Обозначение орта вектора.
15
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 9, с.17
Определения
1.Определение угла между двумя векторами.
2.Определение угла между вектором и осью.
3.Определение координатного угла в ДСК на плоскости.
4.Определение абсциссы и ординаты точки координатной плоскости.
5.Определение координат точки координатной плоскости.
6.Определение координатной плоскости.
7.Определение ПДСК на плоскости.
8.Определение радиус-вектора точки координатной плоскости.
9.Определение координат вектора на координатной плоскости.
10.Определение координатной формы записи вектора координатной плоскости.
11.Определение направляющих углов и направляющих косинусов вектора координатной плоскости.
12.Определение орта вектора.
Теоремы
1.Теорема о вычислении проекции вектора на ось.
2.Теорема о координатах точки и её радиус-вектора.
3.Теорема о равенстве векторов в координатной форме записи.
4.Теорема о действиях с векторами в координатной форме записи.
5.Теорема о вычислении координат вектора.
6.Формула расстояния между двумя точками плоскости.
7.Формула модуля вектора, заданного в координатной форме.
8.Формула направляющих косинусов вектора, заданного в координатной форме.
9.Формулы координат точки, делящей данный отрезок в данном отношении.
10.Формулы координат середины отрезка.
11.Формулы вычисления отношения, в котором данная точка делит данный отрезок.
Тест 9
1.Отметьте на координатной плоскости Оху следующие точки: А(3; 4), В(–1; 2), С(–1; –2), D(3; –4).
2.Отметьте на координатной плоскости Оху точки, симметричные точке А(2; 4) относительно осей координат и начала координат.
3.Отметьте на координатной плоскости Оху точки, симметричные точке А(2; 4) относительно биссектрисы координатного угла и бис-
16

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 9, с.17
сектрисы угла, смежного с координатным.
4.Найдите координаты радиус-вектора точки А(2; 5) и изобразите его на координатной плоскости.
5.Отложите от точки А(–2; –3) вектор a ( 2;3) и найдите координаты его конца.
6.Найдите модуль и направляющие косинусы вектора a ( 4;3) .
7.Запишите в координатной форме орт вектора a (4; 3) .
8.Запишите вектор AB в координатной форме записи, если А(–5; –8),
В(–8; 5).
9. Найдите расстояние между точками |
|
|
1 |
; |
2 |
|
и |
|
|
4 |
; |
3 |
|
, и |
A |
2 |
3 |
|
B |
3 |
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
координаты середины отрезка АВ.
10. На отрезке АВ найдите точку, которая делит его в отношении
|
|
5 |
|
|
1 |
; |
2 |
|
|
4 |
; |
3 |
|
|
, считая от точки A |
2 |
|
, если B |
3 |
. |
|||||
|
|
4 |
|
|
|
3 |
|
|
|
2 |
17
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 10, с.14
Практическое занятие 10 Прямоугольная декартовая система координат в
пространстве
Краткое содержание: ориентация трех взаимно перпендикулярных координатных осей в пространстве, координаты точки и ПДСК в пространстве, координаты вектора и координатная форма записи, действия с векторами в координатной форме, расстояние между двумя точками в пространстве, модуль вектора, его направляющие углы и косинусы, орт вектора, деление отрезка в данном отношении.
п.1. Теория п.1.1. Ориентация координатных осей в пространстве
Пусть Ох, Оу и Оz – три взаимно перпендикулярные координатные оси с общим началом координат в точке их пересечения О. Ось Ох называется осью абсцисс, ось Оу – осью ординат, ось Оz – осью аппликат.
Рассмотрим кратчайший поворот оси Ох вокруг начала координат в плоскости Оху к оси Оу, причем наблюдать за этим поворотом будем из той части полупространства относительно плоскости Оху, в которой находится положительная полуось аппликат. Если наблюдаемый поворот осуществляется против часовой стрелки (смотрите рисунок 1), то говорят, что оси координат имеют правую ориентацию, иначе (смотрите рисунок 2) – левую.
z
О у
у
х
Рис. 1
п.1.2. Прямоугольная декартовая система координат в пространстве
Пусть Ох, Оу, Оz – три взаимно перпендикулярные оси с правой ориентацией, с общим началом координат О и общим масштабом. Введем понятие координат произвольной точки пространства М. Пусть Mx , My , Mz – проекции точки М на координатные оси Ох, Оу, Оz со-
1
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 10, с.14
ответственно. Смотрите рисунок 3.
z
О х
х
у
Рис. 2
z 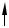 Mz
Mz
М
О |
у |
|
|
Mx |
My |
|
|
х |
|
Рис. 3
Каждая точка на координатной оси имеет координату. Обозначим xM , yM , zM координаты точек Mx , My , Mz на координатных осях Ох,
Оу, Оz соответственно, т.е. Mx (xM ), My (yM ), Mz (zM ) .
Определение. Числа xM , yM , zM называются, соответственно, абс-
циссой, ординатой и аппликатой точки М. Упорядоченный набор чисел (xM , yM , zM ) называется координатами точки М.
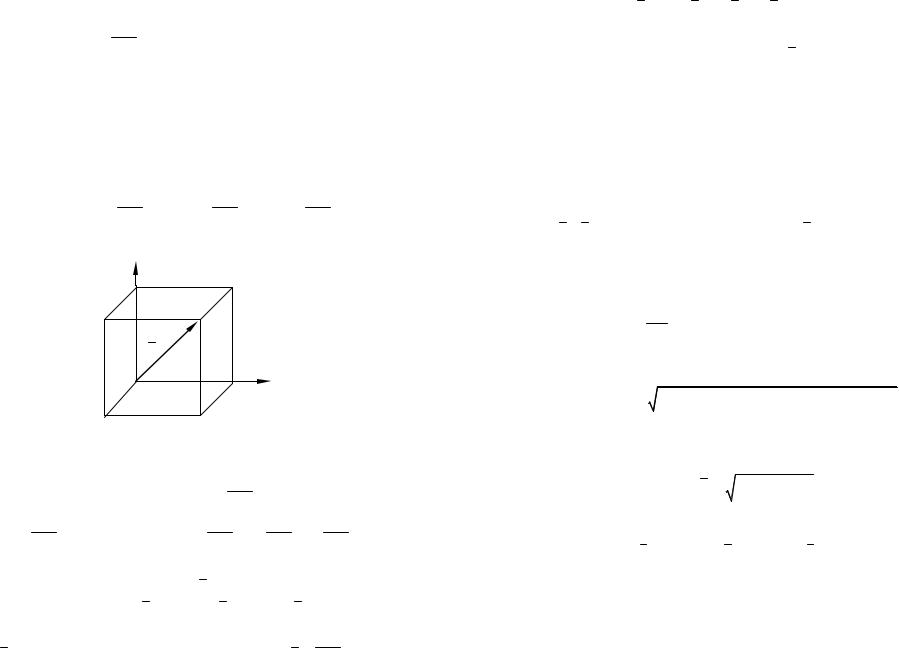
Общепринято следующее обозначение координат точки М: M(xM , yM , zM ) . (Смотрите рисунок 4.)
Определение. Прямоугольной декартовой системой координат в пространстве называются три взаимно перпендикулярные оси с правой ориентацией, с общим началом координат, общим масштабом и вве-
2
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 10, с.14
денным понятием координат любой точки пространства.
п.1.3. Координаты вектора и его координатная форма записи
Определение. Вектор OM , где О – начало координат, называется ра- диус-вектором точки М.
Определение. Координатами вектора называются его проекции на координатные оси.
Теорема. (О координатах точки и ее радиус-вектора.) Координаты точки М в ПДСК в пространстве совпадают с координатами её ради- ус-вектора:
xM прx OM, yM прy OM, zM прz OM .
Смотрите рисунок 4.
z
Mz (zM )
M(xM , yM , zM )
a
О
у
My (yM )
х Mx (xM )
Mx (xM )
Рис. 4
Принято отождествлять радиус-вектор OM с упорядоченной тройкой его координат:
OM (xM , yM , zM ) (прx OM, прy OM, прz OM) .
Введем для произвольного вектора a обозначения:
ax прx a, ay прy a, az прz a .
Пусть a – произвольный вектор пространства и a OM . Так как проекции вектора на оси не зависят от выбора точки его начала, то можно
3
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 10, с.14
записать:
a (прx a, прy a, прz a) (ax , ay , az ) .
Определение. Запись вектора в виде a (ax , ay , az ) называется его координатной формой записи.
Теорема. (О равенстве векторов.) Два вектора равны тогда и только тогда, когда равны их координаты.
Теорема. (О действиях с векторами в координатной форме.) При сложении векторов их координаты складываются, а при умножении вектора на число каждая координата вектора умножается на это число:
a b (ax bx , ay by , az bz ) , k a (k ax , k ay , k az ) .
Теорема. (О вычислении координат вектора.)
Для того, чтобы вычислить координаты вектора нужно из координат его конца вычесть координаты его начала:
AB (xB xA ; yB yA ; zB zA ) .
Теорема. (Формула расстояния между двумя точками.) AB (xB xA )2 (yB yA )2 (zB zA )2 .
Теорема. (О модуле вектора.) Модуль вектора равен корню квадратному из суммы квадратов его координат.
| a | a2x a2y az2 .
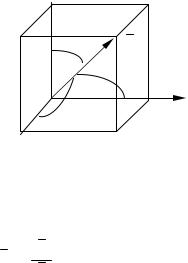
Обозначим углы между вектором и координатными осями: (a ^ Ox) , (a ^ Oy) , (a ^ Oz) .
Определение. Углы между вектором и координатными осями называются его направляющими углами, а косинусы этих углов называются направляющими косинусами.
Теорема. (О направляющих косинусах вектора.) Пусть
4
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 10, с.14
a |
(ax ; ay ; az ) . Тогда |
|
|
|
|
|
|
|
|
|
|||||
|
cos |
a |
x |
, cos |
ay |
, cos |
a |
z |
, cos2 cos2 cos2 1. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
| a | |
| a | |
| a | |
||||||||||||
|
|
|
|
|
|||||||||||
z 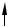
a
О |
|
у |
х
Рис. 5
Теорема. (Об орте вектора.) Направляющие косинусы вектора являются декартовыми координатами его орта:
ao | aa | (cos ; cos ; cos ) .
п.1.4. Деление отрезка в данном отношении Теорема. (О координате точки, делящей отрезок.) Пусть
A(xA , yA , zA ), B(xB , yB , zB ) и C(xC , yC , zC ) – три произвольные точ-
ки пространства, лежащие на одной прямой L и точка С делит отрезок
АВ в отношении CAB , считая от точки А. Тогда |
|
|||||||||||||||||
xC |
xA xB |
, yC |
|
yA yB |
|
, zC |
zA zB |
и |
||||||||||
|
|
|
|
|
|
1 |
1 |
|||||||||||
|
1 |
|
|
|
|
|
|
|
|
|||||||||
|
CAB |
xC xA |
|
yC yA |
|
zC zA |
. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
xB xC |
|
|
|
yB yC |
|
|
zB zC |
|
|||||||
Следствие. Если точка С есть середина отрезка АВ, то |
|
|||||||||||||||||
xC |
xA xB |
, yC |
|
|
yA yB |
|
, zC |
zA zB |
. |
|
||||||||
|
|
|
|
|
||||||||||||||
2 |
|
|
2 |
|
2 |
|
|
|||||||||||
5
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 10, с.14
п.2. Список задач Список №1
1.Построить чертеж ПДСК в пространстве, и отметить на нем точку с заданными положительными координатами.
2.Найти в координатном пространстве координаты точки, симметричной данной относительно координатных плоскостей, координатных осей и начала координат.
3.Найти расстояние от данной точки до координатных плоскостей и координатных осей.
4.Построить в ПДСК Oxyz радиус-вектор точки с заданными координатами, и найти его проекции на координатные оси.
5.Дан вектор в координатной форме записи. Найти его модуль и направляющие косинусы. Записать орт данного вектора в координатной форме.
6.Дан орт вектора и его модуль. Найти его координаты, и записать в координатной форме.
7.Дан модуль вектора и два из трех направляющих углов. Найти координаты вектора.
8.Найти координаты вектора по известным координатам его начала и конца.
9.Найти координаты суммы векторов и произведения вектора на число.
10.Найти расстояние между двумя точками с известными координатами.
11.Найти отношение, в котором данная точка делит данный отрезок.
12.На данном отрезке найти координаты точки, делящей данный отрезок в данном отношении.
13.Найти координаты середины отрезка.
Список №2
1.Найти на координатных осях точку, удаленную от данной точки на данное расстояние.
2.Точка с одной известной координатой делит данный отрезок в данном отношении. Найти неизвестные координаты этой точки.
п.3. Примеры Пример 1. Построить точку М(1; 2; 2) в координатном пространстве
Oxyz, и найти расстояния от неё до координатных плоскостей и осей. Решение. Смотрите рисунок 6.
6
