
АГ ПЗ 1-35 (полный вариант)
.pdf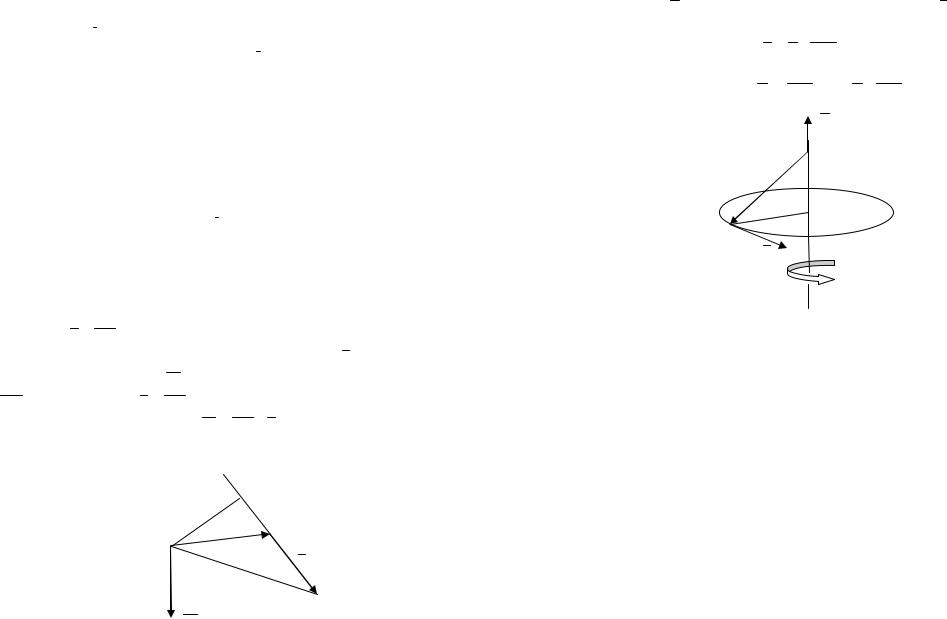
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 16, с.10
п.1.2. Векторное произведение в координатной форме |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Теорема. |
|
Пусть |
|
|
векторы |
|
|
заданы |
|
в |
координатной форме: |
||||||||||||||||||||||||||||||||||||||||||
|
a |
(x1 , y1 , z1 ), |
b |
(x2 , y2 , z2 ) . Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
k |
|
|
|
|
y1 |
z1 |
|
i |
|
x1 |
z1 |
|
|
|
|
|
x1 |
y1 |
|
|
|
|
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
y |
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
a |
b |
1 |
|
|
|
|
|
|
|
j |
k |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
y2 |
z2 |
|
|
|
|
x2 |
z2 |
|
|
|
|
|
x2 |
y2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
y2 |
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
п.1.3. Применение векторного произведения векторов |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
1. Вычисление площади треугольника. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
Пусть |
|
|
|
даны |
|
|
|
|
|
|
координаты |
|
вершин |
1 | |
|
треугольника: |
|||||||||||||||||||||||||||||||||||
|
A(x |
, y , z ), B(x |
|
, y |
|
|
, z |
|
|
), C(x |
|
, y |
, z |
|
) . Тогда S |
|
|
|
| , где |
||||||||||||||||||||||||||||||||||
|
2 |
2 |
2 |
3 |
3 |
AB |
AC |
||||||||||||||||||||||||||||||||||||||||||||||
1 |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
ABC |
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
j |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 x1 |
|
y2 y1 |
z2 z1 |
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
AB |
AC |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 x1 |
|
y3 y1 |
z3 z1 |
|
|
|
|
|
|
|
|
|
||||||||||||||
2. Вычисление момента силы относительно точки.
Пусть F AB – вектор силы, приложенный к точке А и пусть С –
произвольная точка. В механике моментом силы F относительно точки С называется вектор M равный векторному произведению вектора CA на вектор силы F AB :
M CA F .
Величина момента равна величине силы на плечо h M F h .
h
A
C
F
B
M
Рис.2.
3
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 16, с.10
3. Вычисление линейной скорости точки тела вращения.
Пусть М точка тела, вращающегося вокруг некоторой оси с угло-
вой скоростью , О – произвольная точка этой оси, v – вектор линейной скорости точки М. Тогда
v OM .
Величина линейной скорости
v r | | | OM | sin ( ^ OM) .
О
r
М
v
Рис.3.
п.2. Список задач Список №1
1.Построить векторное произведение двух данных векторов.
2.Вычислить модуль векторного произведения векторов, если известны их модули и угол между ними.
3.Задачи на использование свойства линейности векторного произведения.
4.Вычислить векторное произведение векторов заданных в координатной форме.
5.Вычислить модуль векторного произведения векторов, заданных в координатной форме.
6.Вычислить синус угла между векторами заданными в координатной форме.
7.Вычислить площадь треугольника с известными координатами его вершин.
8.Вычислить момент силы относительно точки.
Список №2
1. Найти вектор, ортогональный двум данным векторам.
4

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 16, с.10
п.3. Примеры |
|
|
|
|
|
|
||||||||||||||||||||||
Пример 1. Угол между векторами |
|
и |
|
|
равен |
. Зная, что |
||||||||||||||||||||||
a |
b |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
| |
a |
| 6, | |
b |
|
| 5 , вычислить | |
a |
|
b |
| . |
|
|
|
|
|
|
|||||||||||||
Решение. | |
|
|
|
| | |
|
| | |
|
|
|
^ |
|
|
|
15 . Ответ: 15. |
||||||||||||||
a |
b |
a |
b |
| sin (a |
b) 6 5 sin |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
Пример 2. Векторы a и b ортогональны. Зная, что | a | 3, | b | 4 , вы-
числить | (a b) (a b) |.
Решение. Вычисляем векторное произведение, стоящее под знаком модуля, используя свойство линейности векторного произведения. Раскрываем скобки, сохраняя порядок сомножителей:
(a b) (a b) a a a b b a b b .
Так как a || a и b || b , то по свойству векторного произведения
a a b b 0 . По свойству антикоммутативности b a a b . Получаем
(a b) (a b) a b a b 2a b ,
| (a b) (a b) | | 2a b | 2 | a b | 2 | a | | b | sin(a ^ b)
2 3 4 sin |
|
24. |
|
Ответ: 24. |
|
|||
|
2 |
|
|
|
|
|
3 |
|
Пример 3. |
Угол между векторами |
|
и |
|
равен |
. Зная, что |
||
a |
b |
|||||||
|
|
|
|
|
|
|
4 |
|
| a | 3, | b | 2 2 , вычислить ((2a b) (2a b))2 .
Решение. Выражение, которое нам нужно вычислить есть скалярный квадрат вектора c (2a b) (2a b) .
Раскрываем скобки:
c(2a b) (2a b) (2a) (2a) (2a) b b (2a) b b .
4(a b).
Находим модуль вектора c : |
2 sin 3 24 . |
| c | | 4(a b) | 4 | a | | b | sin (a ^ b) 4 3 2 |
4
Вычисляем скалярный квадрат вектора c : 5
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 16, с.10
c2 | c |2 242 576 .
Ответ: 576.
Пример 4. Вычислить векторное произведение векторов a (7; 2; 2), b ( 3; 0;1) .
Решение. Воспользуемся формулой вычисления векторного произведения векторов, заданных в координатной форме:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
j |
k |
|
|
|
|
i |
|
j |
|
k |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
x1 |
y1 |
z1 |
|
|
|
7 2 |
|
2 |
|
||||||||||||||
|
|
a |
b |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x2 |
y2 |
z2 |
|
|
|
|
3 |
0 |
1 |
|
|
|
|
|
|||||||||
|
2 |
2 |
|
|
7 |
|
2 |
|
|
|
|
|
7 2 |
|
|
|
|
|
|
|
||||||||||||
|
|
i |
|
|
|
|
|
|
|
|
|
2i |
|
|
|
|
||||||||||||||||
|
|
j |
|
|
|
k |
j 6k. |
|||||||||||||||||||||||||
|
0 |
1 |
|
|
|
|
3 |
1 |
|
|
|
|
|
|
|
3 0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: a b (2; 1;6) .
Пример 5. Даны точки А(0; 1; 2), В(–3; 3; 0) и С(6; 5; 2). Вычислить площадь треугольника АВС.
Решение. Площадь треугольника АВС находим по формуле: S ABC 12 | AB AC | .
Вычисляем координаты векторов AB и AC : AB ( 3;2; 2), AC (6;4;0) .
Вычисляем векторное произведение AB AC :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
j |
k |
|
|
|
|
|
2 |
|
|
2 |
|
|
|
3 |
2 |
|
|
|
|
3 |
2 |
|
|
|
|||||||||||||
|
|
|
|
|
3 |
2 |
2 |
|
|
|
|
i |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
AB |
AC |
j |
k |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
6 |
4 |
0 |
|
|
|
|
|
|
4 |
0 |
|
|
|
|
6 |
0 |
|
|
|
|
6 |
4 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
8i 12j |
24k 4(2i 3j 6k) . |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Вычисляем модуль вектора |
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
AB |
AC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
| |
|
|
|
| 4 22 32 62 4 7 28 . |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
AB |
AC |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Находим площадь треугольника: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
S |
1 | |
|
|
|
| 14 . |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
AB |
AC |
|
|
|
|
|
|
|||||||||||||||||||||||||||
ABC |
2 |
|
Ответ: 14. |
||
|
||
|
6 |

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 16, с.10
Пример 6. Дано: | a | 3, | b | 26 и | a b | 72 . Вычислить a b .
Решение. Из определения векторного произведения находим синус угла между векторами:
|
|
|
|
|
| |
a |
|
b |
| |
|
72 |
12 . |
|||||
sin (a |
^ b) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
| a | | b | |
|
3 26 13 |
||||||||||
Используя основное тригонометрическое тождество, находим косинус угла между векторами и искомое скалярное произведение:
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
12 |
2 |
|
5 |
|
|||||
cos(a ^ b) |
1 sin |
(a ^ b) 1 |
|
|
, |
||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
13 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
a b | a | | b | cos(a ^ b) 3 26 |
|
|
|
|
30 . |
|
|||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|||
Ответ: a b 30 .
п.4. Задачи Задачи для аудиторного решения 16
1. Изобразить два произвольных вектора, отложенные от одной точки
под углом 45o между ними. Построить векторные произведения этих векторов.
2. |
|
Угол |
между |
|
|
векторами |
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
равен |
5 . |
Зная, |
что |
|||||||||||||||||||||||||||||||||||||||||
a |
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
| 2 |
6, | |
|
|
| 7 |
|
|
2 , вычислить | |
|
|
|
|
|
|
| . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
a |
b |
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
3. |
Угол между векторами |
|
|
и |
|
|
|
|
|
|
равен |
|
2 |
. Зная, что | |
|
|
| 1, | |
|
| 2 , |
||||||||||||||||||||||||||||||||||||||||||||||
a |
b |
|
|
|
|
a |
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
вычислить: а) (a |
b)2 ; б) ((2a b) (a 2b))2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
4. |
Даны |
векторы |
|
|
|
|
(3; 1; 2), |
|
(1; 2; 1) . Найти: а) |
|
|
|
|
; |
б) |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
a |
b |
a |
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
(2a |
b) b ; в) (2a b) (2a b) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
5. |
Даны векторы |
|
(3; 1; 2), |
|
(1; 2; 1) . Найти | |
|
|
|
| |
и синус уг- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
a |
b |
a |
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ла между данными векторами. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
6.Даны точки А(1; 2; 0), В(3; 0; –3) и С(5; 2; 6). Вычислить площадь треугольника АВС.
7.Сила P (2; 4; 5) приложена к точке М(4; –2; 3). Найти момент этой силы относительно точки А(3; 2; –1).
7
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 16, с.10
Задачи повышенного уровня сложности 16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
8. |
Вектор |
|
|
, ортогональный векторам |
|
(4; 2; 3) |
|
и |
|
|
|
(0;1; 3) об- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x |
a |
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
разует с осью Оу тупой угол. Зная, что | |
|
|
|
|
|
|
| 26 , найти его коорди- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
наты. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
9. |
Найти вектор |
|
|
|
|
, зная, что он ортогонален векторам |
|
(2; 3;1) |
и |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x |
a |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
(1; 2; 3) и удовлетворяет условию |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
b |
x |
(i 2j |
7k) 10 . |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Домашнее задание 16. Векторное произведения векторов |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1. Постройте чертеж ПДСК Oxyz и орты i, |
|
|
|
|
|
|
|
|
|
|
координатных осей. На |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
j,k |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
этом же |
|
|
чертеже изобразите вектор |
|
i |
|
|
|
и постройте векторы |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
j |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
i (i |
|
|
|
|
и (i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
j) |
|
j) k , найдите их модули, используя только опреде- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ление векторного произведения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
2. Дано: | |
|
| 2, | |
|
|
|
|
|
|
^ |
b) . Найти | |
|
|
|
|
| . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
a |
b |
|
| 3, (a |
a |
b |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
3. |
Векторы |
a |
|
и |
b |
ортогональны. Зная, что | |
a |
| | |
b |
| 10 , вычислить: а) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
| (a |
b) (a b) |; б) | (3a b) (a 2b) | . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
4. |
|
|
Найти |
|
|
|
векторное произведение |
векторов |
|
|
( 1;2; 2) |
и |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
a |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b(2; 2;1) .
5.Даны вершины треугольника А(1; –1; 2), В(5; –6; 2) и С(1; 3; –1). Вычислить длину его высоты, опущенной из вершины В на сторону АС.
Самостоятельная работа 16
Вариант 1.
1.Геометрический смысл модуля векторного произведения.
2.a b, | a | | b | 1. Найдите | (3a) (a b) | .
3. Даны точки А(–1; –2; 4), В(–4; –2; 1) и С(3; –1; 4). Найдите | AB AC | .
Вариант 2.
1.Ориентация тройки {a, b, a b}.
2.a b, | a | | b | 1. Найдите | (a b) (2b) |.
3.Даны точки А(1; –2; 2), В(1; 4; 0), С(–4; 1; 1). Найдите | BC BA | .
8
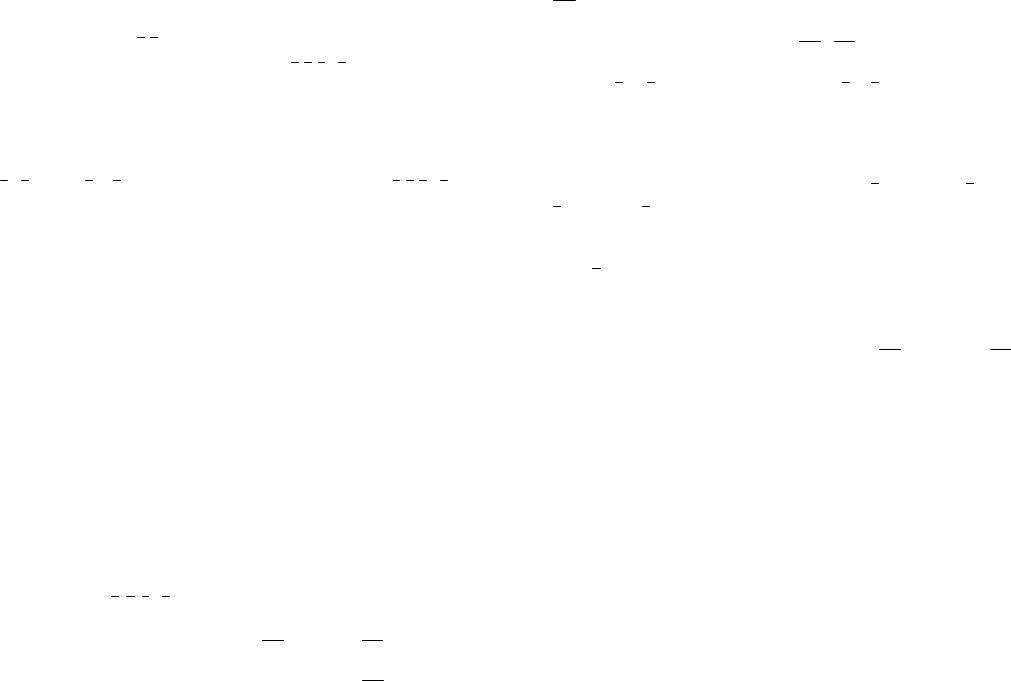
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 16, с.10
Вариант 3.
1.Определение момента силы относительно данной точки.
2.Система векторов {a,b} образует ортонормированный базис на
плоскости. Образует ли тройка векторов {a,b,a b} ортонормированный базис пространства? Ответ обоснуйте.
3.Найдите площадь треугольника АВС, если А(2; –3), В(3; 2), С(–2; 5).
Вариант 4.
1. Определение векторного произведения двух векторов.
2. (a ^ b) 45o , | a | | b | 1. Образует ли тройка векторов {a,b,a b}
нормированный базис пространства? Ответ обоснуйте.
3.Найдите площадь треугольника АВС, если А(–3; 2), В(5; –2), С(1; 3).
п.5. Вопросы и задачи для самоконтроля 16 Обозначения
1. Обозначение векторного произведения.
Определения
1. Определение векторного произведения векторов.
Теоремы
1.Простейшие свойства векторного произведения.
2.Свойство линейности векторного произведения.
3.Формула вычисления векторного произведения векторов, заданных
вкоординатной форме.
4.Вычисление момента силы относительно точки.
Тест 16 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
, | |
|
| 3, | |
|
| 2 . Вычислить | |
|
|
|
| и изобразить на |
|
1. Дано: (a |
^ b) |
a |
b |
a |
b |
|||||||||
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
рисунке векторы a, b, a b , отложив их от одной точки.
2.Дан правильный треугольник АВС со стороной 1. Вычислите модуль векторного произведения вектора AB на вектор BC .
3.Пусть BD – высота правильного треугольника АВС со стороной 1.
Вычислите модуль векторного произведения вектора AB на вектор
9
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 16, с.10
BD .
4.Дан квадрат ABCD со стороной 1. Изобразите на чертеже данный квадрат и векторное произведение AC AB , отложив его от точки А, вычислите его модуль.
5. Векторы a и b ортогональны. Зная, что | a | | b | 10 , вычислить: а)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| (a |
b) (a b) |; |
б) | (3a b) (a 2b) | . |
|
|
|
|
||||||||||||||||||||
6. Даны векторы: |
|
(3; 1; 2), |
|
(1; 2; 1) . Найти: а) |
|
|
|
; б) |
||||||||||||||||||
a |
b |
a |
b |
|||||||||||||||||||||||
| |
|
|
|
| . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
7. Вычислите векторное произведение вектора a на вектор b , если
a(1; 2; 2), b (2; 2;1) .
8.С помощью векторного произведения двух векторов найдите пло-
щадь треугольника А(–1; 2; –2), В(0; 4; –7), С(0; –5; 8).
9.Сила P (2; 4;5) приложена к точке М(4; –2; 3). Найдите момент этой силы относительно точки А(3; 2; –1).
10.В ПДСК Охуz дан тетраэдр ОАВС и координаты его вершин: А(1; 0; 0), В(0; 4; 0), С(0; 0; 2). Постройте чертеж, и изобразите на этом
же чертеже векторное произведение вектора OB на вектор OC . Найдите координаты этого векторного произведения.
10

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 17, с.11
Практическое занятие 17 Смешанное произведение векторов
Краткое содержание: определение и простейшие свойства смешанного произведения, модуль и знак смешанного произведения, перестановка векторов в смешанном произведении, свойство линейности смешанного произведения, смешанное произведение векторов в координатной форме, вычисление объема пирамиды.
п.1. Теория п.1.1. Определение и свойства смешанного произведения
Определение. Смешанным произведением упорядоченной тройки
векторов (a, b, c) называется скалярное произведение первого вектора на векторное произведение второго вектора на третий и обозначается a b c a (b c) .
Теорема. (Геометрический смысл смешанного произведения.)
1) Модуль смешанного произведения трех векторов численно равен объему параллелепипеда, построенного на трех данных векторах, как на его ребрах:
| a b c | V(a, b, c) .
2) Тройка векторов {a, b, c} – правоориентированная тогда и только тогда, когда a b c 0 .
3) Тройка векторов {a, b, c} – левоориентированная тогда и только тогда, когда a b c 0 .
4) Тройка векторов {a, b, c} – компланарная тогда и только тогда, ко-
гда a b c 0 .
Определение. Любое изменение порядка следования векторов в трой-
ке векторов {a, b, c} называется её перестановкой.
Определение. Транспозицией в тройке векторов {a, b, c} называется
такая её перестановка, при которой только один из векторов остается на своём месте, а два других вектора меняются местами.
Определение. Круговой перестановкой тройки векторов {a, b, c} на-
зывается такая её перестановка, при которой ни один из векторов не остается на своём месте.
1
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 17, с.11
a
c
b
Рис.1.
Лемма. Круговая перестановка в тройке векторов не изменяет её ориентацию, а транспозиция любых двух векторов данной тройки изменяет её ориентацию на противоположную.
Следствие.
1)a b c с a b b c a ;
2)a b c b a c c b a a c b ;
3)a b c (a b) c .
Теорема. (Свойство линейности смешанного произведения.) Для любых векторов и действительных чисел справедливы следующие равенства:
1)(a1 a2 ) b c a1 b c a2 b c ;
2)( a) b c (a b c) ;
3)a (b1 b2 ) c a b1 c a b2 c ;
4)a ( b) c (a b c) ;
5)a b (c1 c2 ) a b c1 a b c2 ;
6)a b ( c) (a b c) .
п.1.2. Смешанное произведение векторов в координатной форме
Теорема. Пусть a (x1 , y1 , z1 ), b (x2 , y2 , z2 ), c (x3 , y3 , z3 ) .
Тогда
2

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 17, с.11
x1 y1 z1
a b c x2 y2 z2 . x3 y3 z3
п.1.3. Применение смешанного произведения векторов
1. Вычисление объема параллелепипеда ABCDA1B1C1D1 :
V| AB AD AA1 | .
2.Вычисление объема треугольной пирамиды SАВС:
V16 | AB AC AS | .
3.Вычисление высоты треугольной пирамиды SАВС, опущенной из вершины S:
H | AB AC AS | . | AB AC |
п.2. Список задач Список №1
1.Определить ориентацию данной тройки векторов, используя свойства смешанного произведения.
2.Вычисление смешанного произведения с использованием его определения и свойств.
3.Вычислить смешанное произведение векторов, заданных в координатной форме.
4.Определить ориентацию данной тройки векторов, заданных в координатной форме.
5.Выяснить, компланарная ли данная тройка векторов, если известны их координаты.
6.Выяснить, лежат ли данные четыре точки с известными координатами в одной плоскости.
7.Вычислить объем тетраэдра с известными координатами его вершин.
8.Найти длину высоты тетраэдра с известными координатами его вершин.
Список №2
1. Задачи на доказательство и повышенного уровня сложности.
3
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 17, с.11
п.3. Примеры
Пример 1. Определить ориентацию тройки векторов: а) {i, j, k} ; б)
{i, k, j} ; в) {j, k, i} .
Решение. а) Определяем ориентацию тройки векторов, используя определение ориентированной тройки векторов.
k
 j
j
i
Рис.2.
Смотрим на рисунке 2 с конца третьего вектора – вектора k , на плоскость, в которой лежат первые два вектора – i и j . Осуществляем кратчайший поворот первого вектора i до совпадения со вторым вектором j и определяем направление вращения – против часовой стрелки. Из определения следует, что данная тройка является правой.
б) Тройка {i, k, j} получается из тройки {i, j, k} транспозицией второго и третьего векторов – j и k . Транспозиция меняет ориентацию тройки векторов. Так как тройка {i, j, k} правая, то отсюда следует, что тройка {i, k, j} является левой.
в) Тройка {j, k, i} получается из тройки {i, j, k} круговой перестановкой. Вектор i с первого места переходит на третье, сдвигая векторы j и k влево. Круговая перестановка не меняет ориентацию тройки векторов, следовательно, тройка {j, k, i} является правой, как и тройка
{i, j, k} .
Ответ: а), в) тройка правая; б) тройка левая.
Пример 2. Векторы a, b, c образуют левую тройку и взаимно ортого-
нальны. Вычислить a b c , если | a | 4, | b | 2, | c | 3.
Решение. По теореме о геометрическом смысле смешанного произве- 4
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 17, с.11
дения
| a b c | V(a,b,c) .
Так как параллелепипед прямоугольный, то его объем равен произведению длин трех его ребер пересекающихся в одной вершине, т.е. произведению модулей векторов, на которых он построен:
V(a,b,c) | a | | b | | c | 4 2 3 24 .
По условию задачи тройка векторов {a, b, c} левая, следовательно, по той же теореме, a b c 0 . Число, равное смешанному произведению a b c отрицательное, а его модуль равен 24, т.е. a b c 24 .
Ответ: a b c 24 .
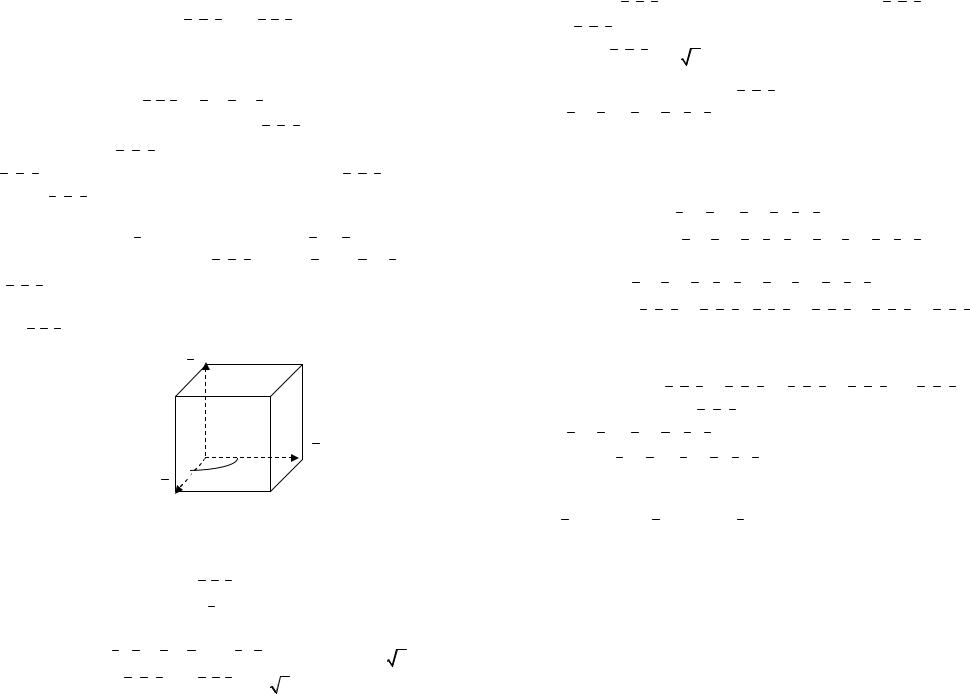
Пример 3. Вектор c ортогонален векторам a и b , угол между которыми равен 45o . Вычислить a b c , если | a | 6, | b | | c | 3 , тройка
{b, a, c} левая.
Решение. По условию задачи параллелепипед, построенный на векторах a,b,c , является прямым. Смотрите рисунок 3.
c
b
135o
a
Рис.3.
Объем параллелепипеда равен произведению площади основания на высоту:
V(a, b,c) Sосн H .
Высота параллелепипеда H | c | 3 . Основанием параллелепипеда является параллелограмм, площадь которого
Sосн | a b | | a | | b | sin (a ^ b) 6 3 sin135o 9 2 . Отсюда находим | a b c | V(a,b,c) 27 2 .
5
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 17, с.11
Тройка {b, a, c} левая, следовательно, тройка {a, b, c} является правой и a b c 0 .
Ответ: a b c 27 2 .
Пример 4. Известно, что a b c 17 . Вычислить
(a 2b) (3a 4b c) c .
Решение. Воспользуемся свойством линейности смешанного произведения, т.е. возможностью раскрывать скобки и выносить скалярные множители за знак смешанного произведения.
Раскроем первую скобку:
(a 2b) (3a 4b c) c
a (3a 4b c) c 2b (3a 4b c) c
Вкаждом из двух слагаемых раскрываем скобку:
a (3a 4b c) c 2b (3a 4b c) c
3a a c 4a b c a c c 6b a c 8b b c 2b c c
Смешанные произведения, содержащие два одинаковых сомножителя,
равно нулю, так как такие тройки векторов являются компланарными. Убирая из получившейся суммы нулевые слагаемые, получаем
4a b c 6b a c 4a b c 6a b c 10a b c .
По условию задачи a b c 17 , откуда
(a 2b) (3a 4b c) c 170 . Ответ: (a 2b) (3a 4b c) c 170 .
Пример 5. Вычислить смешанное произведение векторов a ( 2; 3;1), b (4;7; 5), c (6; 1;6) .
Решение. Воспользуемся формулой вычисления смешанного произведения векторов, заданных в координатной форме:
|
|
|
|
|
|
|
|
x1 |
y1 |
z1 |
|
|
2 |
|
3 |
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
a |
|
b |
|
c |
|
x2 |
y2 |
z2 |
|
|
4 |
|
|
|
7 5 |
|
|||
|
|
|
|
|
|
|
|
x3 |
y3 |
z3 |
|
|
6 |
|
1 |
6 |
|
|||
|
7 |
5 |
|
|
4 |
5 |
|
|
|
4 |
7 |
|
||||||||
2 |
|
( 3) |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
1 |
6 |
|
|
|
6 |
6 |
|
|
|
6 |
1 |
|
||
6
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 17, с.11
2(42 5) 3(24 30) ( 4 42) 42 .
Ответ: a b c 42 .
Пример 6. Определить, образует ли тройка векторов a (0; 3;1), b (4;0; 5), c (6; 1;0) базис пространства векторов.
Решение. По определению, базисом пространства векторов называется любая упорядоченная некомпланарная тройка векторов. Поэтому дос-
таточно вычислить смешанное произведение a b c данной тройки
векторов. Если a b c 0 , тогда данная тройка векторов является компланарной и не образует базис. В противном случае – образует. Вычисляем смешанное произведение:
|
|
0 |
3 |
1 |
|
|
4 |
5 |
|
4 |
0 |
|
||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
4 |
0 |
5 |
|
3 |
|
86 . |
||||
a |
b |
c |
||||||||||||||||
|
|
|
|
|
|
|
|
6 |
1 |
0 |
|
|
6 |
0 |
|
6 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: да.
Пример 7. Докажите, что следующие четыре точки лежат в одной плоскости: А(–3; 2; –1), В(0; 4; 5), С(2; 2; –1), D(–1; 0; –7) .
Решение. Очевидно, что если векторы AB, AC, AD компланарны, то данные точки лежат в одной плоскости.
С
В
А
D
Рис. 4
Вычисляем координаты векторов AB, AC, AD :
AB (3;2;6), AC (5;0;0), AD (2; 2; 6) .
Вычисляем смешанное произведение:
7
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 17, с.11
|
|
3 |
2 |
6 |
|
||||||
|
|
||||||||||
|
|
|
|
|
|
|
|
5 |
0 |
0 |
0 , ч.т.д. |
AB |
AC |
AD |
|||||||||
|
|
2 |
2 |
6 |
|
||||||
Пример 8. Вычислить объем тетраэдра с вершинами в точках S(–4; 4; –1), А(1; 2; –3), В(3; –2; 2), С(5; –2; 5).
Решение. Вычисляем координаты векторов SA, SB, SC и их смешан-
ное произведение: SA (5; 2; 2), SB (7; 6;3), SC (9; 6;6) ,
|
|
5 |
2 |
2 |
|
||||||
|
|
||||||||||
|
|
|
|
|
|
|
|
7 |
6 |
3 |
84 . |
SA |
SB |
SC |
|||||||||
|
|
9 |
6 |
6 |
|
||||||
Вычисляем искомый объем: V 16 | SA SB SC | 14 . Ответ: 14.
п.4. Задачи Задачи для аудиторного решения 17
1. Определить ориентацию тройки векторов: а) {k, i, j} ; б) {k, j, i} ; в) {j, i, k} ; г) {i j, j, k}; д) {i j, i j, j}; е) {i j, i j, k}.
2.Векторы a, b, c образуют правоориентированный ортогональный базис. Вычислить a b c , если | a | 23 , | b | 52 , | c | 2,1.
3.Вектор c ортогонален векторам a и b , угол между которыми равен
30o . Вычислить |
|
|
|
|
|
, если | |
|
| |
3 |
, | |
|
| |
1 |
, | |
|
| 12 6 . |
|
a |
b |
c |
a |
b |
c |
||||||||||||
4 |
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.Докажите тождество (a b)(b c)(c a) 2abc .
5.Даны три вектора a (1; 1; 3), b ( 2; 2;1), c (3; 2; 5) . Вычислить
a b c и определить ориентацию тройки векторов {a, b, c}.
6.Выяснить, какая из следующих троек векторов является компла-
нарной: а) a (2; 3; 1), b (1; 1; 3), c (1; 9; 11) ;
б) a (3; 2; 1), b (2;1; 2), c (3; 1; 2) ; в) a (2; 1; 2), b (1; 2; 3), c (3; 4; 7) .
8

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 17, с.11
7.Докажите, что четыре точки А(1; 2; –1), В(0; 1; 5), С(–1; 2; 1), D(2; 1; 3) лежат в одной плоскости.
8.Вычислить объем треугольной пирамиды, вершины которой: А(2; – 1; 1), В(5; 5; 4), С(3; 2; –1), D(4; 1; 3).
9.Даны вершины треугольной пирамиды: А(2; 3; 1), В(4; 1; –2), С(6; 3; 7), D(–5; –4; 8). Найти длину ее высоты, опущенной из вершины
D.
10.Объем треугольной пирамиды равен 5, три ее вершины находятся
вточках А(2; 1; –1), В(3; 0; 1), С(2; –1; 3). Найти координаты четвертой вершины D, если известно, что она лежит на оси ординат.
Задачи повышенного уровня сложности 17
11.Докажите, что объем параллелепипеда, построенного на диагоналях граней данного параллелепипеда, равен удвоенному объему данного параллелепипеда.
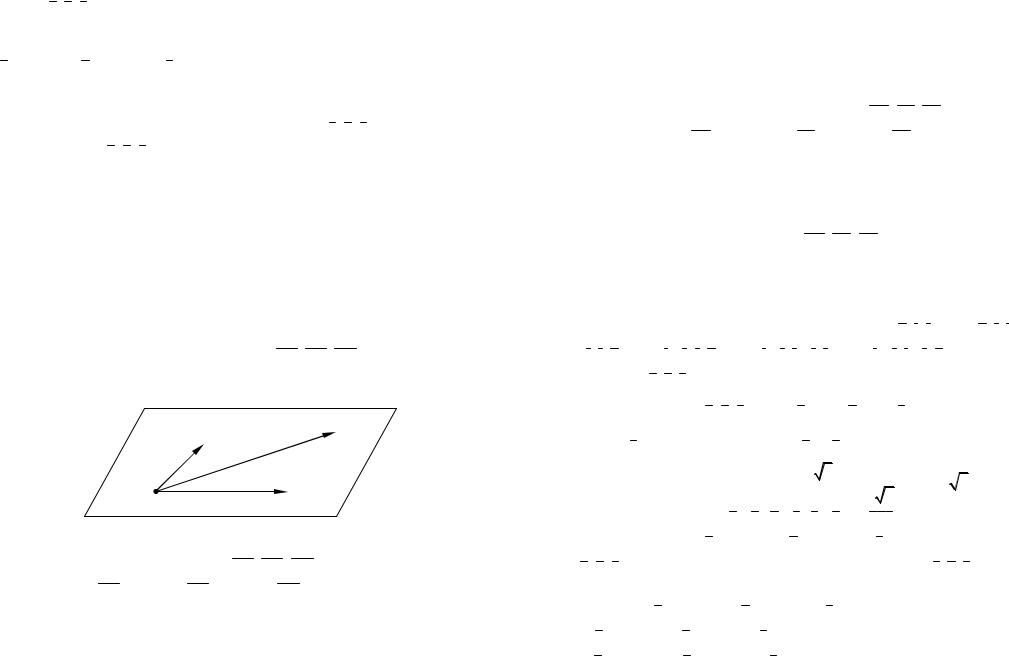
12.Докажите, что для любых векторов a, b, c векторы a b, b c, c a компланарные. Каков геометрический смысл этого факта?
Домашнее задание 17. Смешанное произведение векторов
1. |
Вычислить произведения: а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
b(c a)(b 2c) ; |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
б) (a |
b)(a 2b c)(c a) , если |
a |
|
b |
|
c |
5 . |
|
|
|
|
|||||||||||||||||||||||||
2. |
|
Вычислить объем |
|
параллелепипеда, |
построенного на векторах |
||||||||||||||||||||||||||||||||
|
|
|
( 1; 2; 3), |
|
( 1;1; 2), |
|
(2; 1; 1) . |
|
|
|
|
||||||||||||||||||||||||||
|
a |
b |
c |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) , |
||||
3. |
|
В треугольной |
призме |
|
|
|
|
|
|
векторы AB (0;1; |
|||||||||||||||||||||||||||
|
ABCA B C |
|
|
||||||||||||||||||||||||||||||||||
AC (2; 1; 4) определяют основание, а вектор AA ( 3; 2; 2) направлен по боковому ребру. Найти объем призмы и ее высоту.
Самостоятельная работа 17
Вариант 1.
1.Определение компланарных векторов.
2.Вычислите смешанное произведение векторов a b c , если a b ( 3;3;1), c (4;7; 5) .
3. Определите, компланарны ли векторы a (3;3;1) , b (4;7; 5) , c (2; 1;7) ?
9
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 17, с.11
Вариант 2.
1.Определение смешанного произведения упорядоченной тройки векторов.
2.Вычислите смешанное произведение векторов a b c , если
b c ( 1;4;3), a (14;7; 5) .
3. Определите ориентацию тройки векторов a ( 3; 3;1), b (4;7; 5), c (6; 1;6) .
Вариант 3.
1.Определение правоориентированной упорядоченной тройки векторов.
2.Определите ориентацию тройки векторов
a( 3; 3;1), b (4;7; 5), c (6; 1;6) .
3.Найдите объем тетраэдра АВСD, если А(2; –3; 0), В(3; 0; 2), С(0; –2; 5), D(–7; 7; –3).
Вариант 4.
1.Определение транспозиции в упорядоченной тройке векторов.
2.Определите, компланарны ли векторы
a(3;3;1), b (4;7; 5), c (2; 1;7) ?
3.Найдите объем треугольной пирамиды SАВС, если S(–4; 4; –1), А(1; 2; –3), В(3; –2; 2), С(5; –2; 5).
п.5. Вопросы и задачи для самоконтроля 17 Обозначения
1.Обозначение смешанного произведения.
2.Обозначение объёма параллелепипеда, построенного на трех векторах, как на его ребрах.
Определения
1.Определение смешанного произведения векторов.
2.Определение перестановки в тройке векторов.
3.Определение транспозиции.
4.Определение круговой перестановки.
Теоремы
1.Теорема о геометрическом смысле смешанного произведения.
2.Лемма о перестановках в тройке векторов.
3.Следствие об изменении знака смешанного произведения при пере-
10

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 17, с.11
становках его сомножителей.
4.Следствие о расстановке знаков умножения в смешанном произведении.
5.Свойство линейности смешанного произведения.
6.Формула вычисления смешанного произведения векторов, заданных в координатной форме.
7.Формула объема параллелепипеда с известными координатами его вершин.
8.Формула объема тетраэдра с известными координатами его вершин.
9.Формула длины высоты тетраэдра с известными координатами его вершин.
Тест 17
1. Определить ориентацию тройки векторов:
а) {k, i, j} ; б) {i, k, j} ; в) {j, i, k} ; г) {i j, j, k}.
2.Векторы a, b, c образуют правую тройку и взаимно ортогональны.
Вычислить a b c , если | a | 4, | b | 2 , | c | 3.
3.Дан куб ABCDA1B1C1D1 . Определите ориентацию тройки векторов AB, AC1 , CB1 , и найдите их смешанное произведение.
4.Вычислите (a 2b) (3a 2b c) c , если известно, что a b c 1.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
Вычислите смешанное произведение |
векторов |
a, b и |
c |
, |
если |
|||||||||||||||||||||
|
|
|
(1; 2; 2), |
|
|
(2; 2;1), |
|
(1; 10; 8) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
a |
b |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
6. |
|
|
Определите |
ориентацию тройки |
векторов |
|
|
|
|
|
|
|
|
|
|
если |
|||||||||||
|
|
{a, |
b, c}, |
||||||||||||||||||||||||
|
|
|
(3; 1;1), |
|
( 2;1; 2), |
|
( 2; 3; 5) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
a |
b |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
7. |
|
|
Выяснить, |
компланарные |
ли |
векторы |
|
|
|
|
|
|
|
|
если |
||||||||||||
|
|
|
a, b, c , |
||||||||||||||||||||||||
a(2; 3; 1), b (1; 1; 3), c (1; 9; 11) .
8.Вычислить объем треугольной пирамиды, вершины которой А(2; – 1; 1), В(5; 5; 4), С(3; 2; –1), D(4; 1; 3).
9.Вычислите смешанное произведение векторов правоориентированного ортонормированного базиса. Ответ обоснуйте.
10.Вычислите объем параллелепипеда, построенного на векторах
(i j), j, k как на его ребрах, используя геометрический смысл смешанного произведения векторов и его свойство линейности.
11
