
АГ ПЗ 1-35 (полный вариант)
.pdf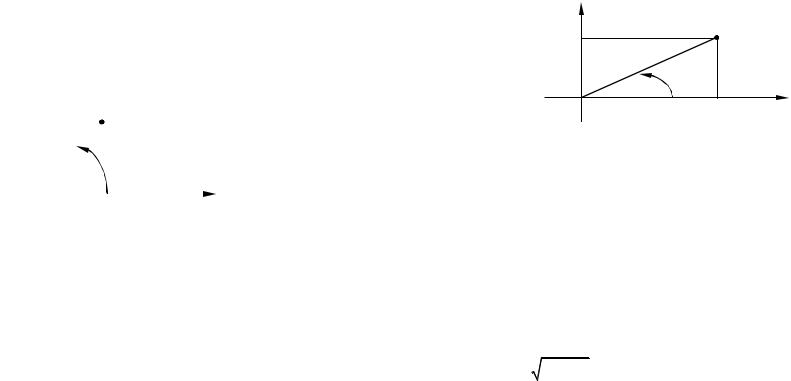
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 12, с.13
Практическое занятие 12 Полярная система координат на плоскости
Краткое содержание: полюс, полярный луч, полярная система координат на плоскости, полярные координаты точки плоскости и их связь с её декартовыми координатами, полярный угол вектора плоскости и его связь с направляющими углами вектора.
п.1. Теория п.1. Полярная система координат на плоскости
Определение. Возьмем на данной плоскости произвольную точку О и назовем её полюсом. Проведем на данной плоскости из точки О направленный луч, который назовем полярным лучом. Пусть М – произвольная точка данной плоскости. Соединим точку М с полюсом отрезком прямой и назовем этот отрезок ОМ и его длину rM OM по-
лярным радиусом точки М. Угол поворота M [0; 2 ) полярного лу-
ча вокруг полюса против часовой стрелки до совпадения с полярным радиусом точки М назовем полярным углом точки М. (Смотрите рисунок 1.)
М
rM M
О
Рис. 1
Определение. Упорядоченная пара действительных чисел (rM ; M ) называется полярными координатами точки М.
Определение. Полярной системой координат на плоскости называется полюс и полярный луч вместе с понятием полярных координат любой точки плоскости.
Замечание. Полярные координаты однозначно определяют положение любой точки на плоскости, за единственным исключением – самого полюса. Чтобы восстановить однозначность для любой точки плоскости полагают полярные координаты полюса равными нулю: О(0; 0). Часто полярный угол рассматривают как в тригонометрии в пределах одного оборота, причем поворот против часовой стрелки
1
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 12, с.13
считают положительным, а по часовой стрелке – отрицательным. Чаще всего полагают, что полярный угол M ( ; ].
п.1.2. Связь полярной и декартовой систем координат на плоскости Определение. Говорят, что ПДСК на плоскости Оху стандартным об-
разом совмещена с полярной системой координат этой же плоскости, если полюс полярной системы координат совпадает с началом координат ПДСК, а полярный луч совпадает с положительной полуосью оси абсцисс Ох.
у
уМ
|
r |
|
|
|
|
|
|
О |
|
х |
х |
|
|
Рис. 2 |
|
Теорема. Пусть ПДСК на плоскости Оху стандартным образом совмещена с полярной системой координат на этой же плоскости. Тогда декартовые координаты (х, у) любой точки плоскости связаны с её полярными координатами (r, ) следующими соотношениями:
x r cosy r sin .
Замечание. Отсюда легко выразить полярные координаты точки через её декартовые координаты:
r |
x |
2 |
y |
2 |
, arctg |
y |
, если |
|
|
|
; |
|
или |
||||
|
|
|
|
2 |
2 |
|
|||||||||||
|
|
x |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
y |
|
|
|
|
|
3 |
|
|
|
||
|
|
|
arctg |
|
, если |
2 |
; |
2 |
. |
|
|
||||||
|
|
|
x |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Если полярный угол лежит в первой или четвертой четверти, т.е.
|
|
; |
|
, то его можно выразить через арксинус: |
|
|
2 |
2 |
|
||
|
|
|
|
||
|
|
|
|
|
2 |

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 12, с.13
arcsin |
y |
|
|
. |
|
x2 y2 |
||
Если полярный угол лежит в первой или второй четверти, т.е.[0; ] , то его можно выразить через арккосинус:
arccos |
y |
|
|
. |
|
x2 y2 |
||
Если же если полярный угол лежит в третьей четверти, т.е.
; 32 , то
arcsin |
y |
2 arccos |
x |
|
|
|
. |
||
x2 y2 |
x2 y2 |
|||
п.1.3. Полярный угол вектора координатной плоскости Определение. Полярным углом вектора координатной плоскости Оху называется угол поворота против часовой стрелки оси абсцисс вокруг любой ее точки до положения сонаправленности с данным вектором.
Замечание. Из определения следует, что полярный угол
[0; 2 ) .
В этом состоит его отличие от просто угла между вектором и осью, (a ^ Ox) [0; ], который изменяется на промежутке от нуля до .
Если отложить вектор от начала координат и ввести полярную систему координат, стандартным образом совмещенную с прямо-
угольной, то полярный угол вектора a OM будет совпадать с полярным углом точки М в полярной системе координат, отчего и происходит название полярного угла вектора. (Смотрите рисунок 3.)
у
М
a
О |
х |
Рис. 3
3
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 12, с.13
Если известны декартовые координаты вектора a (ax ; ay ) , то отло-
жив его от начала координат, получаем радиус-вектор a OM точки его конца – точки М и точка М имеет координаты, совпадающие с координатами ее радиус-вектора: M(ax ; ay ) . Используем связь декарто-
вых координат точки плоскости с полярными. В наших обозначениях: ax | a | cos , ay | a | sin .
Отсюда, получаем выражения для вычисления полярного угла вектора:
cos |aax | , sin |aay| .
Теорема. (О связи между полярным углом вектора и его направляющими углами.) Пусть и направляющие углы вектора a , – его полярный угол. Тогда cos cos , cos sin .
п.2. Список задач Список №1
1.В полярной системе координат построить точки с заданными полярными координатами.
2.Определить полярные координаты точки, симметричной данной относительно полюса и полярного луча.
3.Определить декартовые координаты точки, заданной полярными координатами, если полярная система координат стандартным образом совмещена с прямоугольной.
4.Определить полярные координаты точки, заданной декартовыми координатами, если полярная система координат стандартным образом совмещена с прямоугольной.
5.Найти направляющие углы вектора координатной плоскости и его полярный угол, если вектор задан своими координатами. Построить чертеж, отложив вектор от начала координат.
Список №2
1.Вычислить площадь треугольника, если его вершины заданы своими полярными координатами.
2.Найти формулу расстояния между двумя точками в полярной системе координат.
4

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 12, с.13
3.Вычислить внутренние углы треугольника, если его вершины заданы своими полярными координатами.
4.Найти полярные координаты вершин правильного многоугольника, если полюс полярной системы координат лежит в его вершине, а одна из его сторон лежит на полярном луче.
п.3. Примеры Пример 1. В полярной системе координат на плоскости построить
точки с заданными полярными координатами: A(1; 34 ), B(1;1), C(1; 43 ) .
Ответ: смотрите рисунок 4, где OA OB OC 1.
А |
|
|
3 |
В |
|
A |
|
B 1 |
|
|
|
4 |
||
|
|
|
|
О
C 43
С
Рис. 4
Пример 2. В полярной системе координат на плоскости дана точка
A(1; 34 ) . Постройте точку, симметричную данной относительно по-
люса и полярного луча.
Решение. Смотрите рисунок 5, где OA OB OC 1.
Ответ: точка B(1; 4) симметрична точке А относительно полюса;
точка C(1; 34 ) симметрична точке А относительно полярного луча.
5
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 12, с.13
А |
|
3 |
|
|
|
|
|
A |
|
|
|
||
|
4 |
|
|
|
||
|
|
|
|
|
||
|
|
О |
|
|
|
|
|
|
C |
|
3 |
B |
|
|
|
4 |
||||
|
|
4 |
|
|||
|
|
|
|
|
|
|
С |
В |
|
|
|
Рис. 5 |
Пример 3. В полярной системе координат на плоскости, стандартным образом совмещенной с прямоугольной, найти декартовые координа-
ты точек A(1; 34 ) , B(1;1) и C(1; 23 ) .
Решение. Воспользуемся формулами связи полярных и декартовых координат точки:
|
|
|
|
|
|
|
|
x r |
cos |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Получаем: |
|
|
|
|
|
|
|
y r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xA |
cos |
3 |
|
|
2 |
, yA sin |
|
3 |
|
|
2 |
, |
|
|
|
|
|
|
||||||||
|
|
|
|
|
2 |
|
4 |
|
2 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
||||
xB cos1, yB |
sin1, |
xC cos |
|
|
|
|
|
, yA sin |
|
|
|
|
|
. |
|||||||||||||||
|
2 |
3 |
2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: A( |
2 |
; |
2 |
), B(cos1; sin1), C( 1 ; |
|
|
|
|
3 |
) . |
|
|
|
|
|
|
|
|
|
||||||||||
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример 4. В полярной системе координат на плоскости, стандартным образом совмещенной с прямоугольной, найти полярные координаты
точек: А(1; 1), B( 3;1) , C( 1; 3) , D(3; 4) .
Решение. Для вычисления полярного радиуса точек используем формулу: r x2 y2 . Получаем:
6
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 12, с.13
rA 1 1 2, rB 3 1 2 , rC 1 3 2, rD 9 16 5 .
Для вычисления полярного угла воспользуемся формулой:
arctg |
y |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
, если |
2 |
; |
2 |
|
, |
или |
|
|
||
x |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||
arctg |
|
y |
, если |
|
; |
3 |
|
|
|||||
|
|
|
|
2 |
2 |
. |
|
|
|||||
|
x |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||
Так как точка А лежит в первой четверти, а точка D – в четвертой, то |
|||||||||||||
A arctg1 |
|
|
|
|
4 |
arctg |
4 |
. |
|||||
|
4 |
, D arctg |
3 |
|
3 |
||||||||
|
|
|
|
|
|
|
|
|
|||||
Так как точка В лежит во второй четверти, а точка С – в третьей, то
|
|
|
|
|
|
1 |
|
|
|
|
5 |
|
|
B |
arctg |
|
|
|
6 |
|
6 |
, |
|||
|
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
C arctg |
3 |
|
|
4 . |
|
||||||
|
), B(2; |
5 |
|
4 |
|
|
|
3 |
|
3 |
|
|
Ответ: A( 2; |
), C(2; |
), D(5; arctg |
4) . |
|
||||||||
6 |
3 |
|
||||||||||
|
4 |
|
|
|
|
|
|
3 |
|
|
||
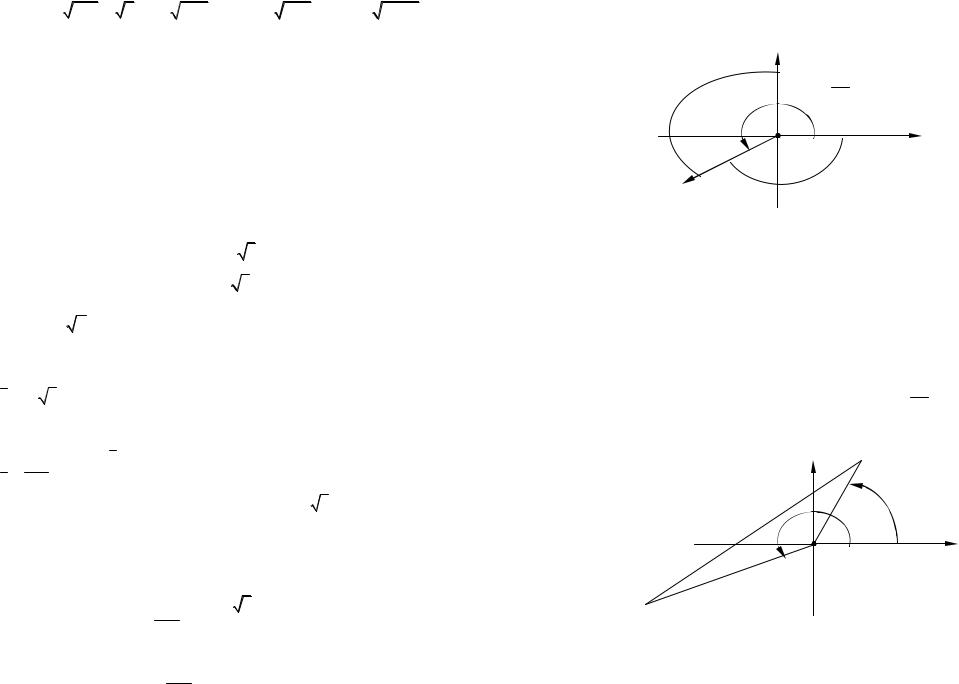
Пример 5. Найти направляющие углы и полярный угол вектора a ( 3; 1) . Отложить вектор от начала координат и построить чер-
теж.
Решение. Построим чертеж (смотрите рисунок 6). Обозначим через М
конец вектора a , отложенного от начала координат. Тогда вектор a OM есть радиус-вектор точки М и координаты точки М совпадают с координатами её радиус-вектора: M( 3; 1) . Тогда полярный
угол вектора, по определению, совпадает с полярным углом точки М в полярной системе координат, совмещенной с прямоугольной. Так как точка М находится в третьей четверти, то её полярный угол равен
M arctg |
1 |
|
|
|
7 . |
|
3 |
6 |
|||||
|
|
|
6 |
Угол между вектором OM и осью Ох равен
56 ,
аугол между вектором OM и осью Оу равен
7
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 12, с.13
|
M |
|
|
7 |
|
|
|
2 . |
|
|
2 |
|
6 |
|
2 |
|
3 |
2 |
у |
|
|
|
|
|
|
|
3M 76
Ох
|
|
|
|
|
a |
|
5 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
М |
6 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
Рис. 6 |
|
|
|
|
|
|
|
|
||
Ответ: полярный угол вектора |
|
равен |
7 |
, |
|
|
^ Ox) |
5 |
, |
|||||||
a |
(a |
|||||||||||||||
6 |
6 |
|||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
^ Oy) |
. |
|
|
|
|
|
|
|
|
|
|
|||
(a |
|
|
|
|
|
|
|
|
||||||||
3 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
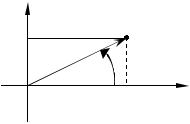
Пример 6. Найти площадь треугольника с вершинами, заданными в полярной системе координат: О(0; 0), A(1; 3) , B(2; 76 ) .
Решение. Смотрите рисунок 7.
|
|
у |
А |
|
|
|
|
|
|
B |
7 |
|
A |
|
6 |
|
3 |
||
|
|
|
х
О
В
Рис. 7
Построим данный треугольник в полярной системе координат Из рисунка видим, что внутренний угол АОВ треугольника равен
8

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 12, с.13
AOB B A 7 5 . 6 3 6
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними:
S OAB 12 OA OB sin( AOB) sin 56 12 .
Ответ: S OAB 12 .
п.4. Задачи Задачи для аудиторного решения 12
1.Построить в полярной системе координат точки, заданные полярными координатами:
|
3; |
|
, B(2; |
|
3; |
|
|
; D(4; 3); Е (1; –1). |
||
A |
2 |
|
), C |
4 |
|
|||||
|
|
|
|
|
|
|
|
|
||
2.Определить полярные координаты точек, симметричных данным относительно полюса и полярной оси:
|
3; |
|
|
2; |
|
|
|
3; |
|
|
, D(5; –2). |
|||
A |
4 |
|
, B |
2 |
|
, C |
3 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
3.Полярная система координат на плоскости совмещена стандартным образом с ПДСК. В полярной системе координат даны точки:
|
6; |
|
, M2 |
(5; 0), M3 |
|
2; |
|
, |
|
|
|
, M5 |
|
8; |
2 |
. Опреде- |
||||
M1 |
2 |
|
|
4 |
|
M4 10; |
3 |
|
|
3 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
лить декартовы координаты этих точек.
4. Полярная система координат на плоскости совмещена с ПДСК. Найти полярные координаты точек, заданных в ПДСК: А(0; 5), В(–
3; 0), C( 3;1), D( 2; |
2) , E(1; 3) . |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
||
5. В полярной системе координат даны две вершины |
A |
3; |
|
|
и |
|||
9 |
||||||||
|
|
|
|
|
|
|
||
|
5; |
3 |
параллелограмма ABCD, точка пересечения диагоналей |
|
B |
14 |
|
||
|
|
|
|
|
которого совпадает с полюсом. Определить две другие вершины этого параллелограмма.
6. В полярной системе координат даны точки |
|
8; |
|
2 |
и |
|
6; |
|
||
A |
3 |
|
B |
3 |
. |
|||||
|
|
|
|
|
|
|
|
|
||
9 |
|
|
|
|
|
|
|
|
|
|
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 12, с.13
Вычислить полярные координаты середины отрезка АВ.
7. Вычислить площадь треугольника ОАВ, где О – полюс полярной
|
|
|
|
|
|
|
|
|
|||
системы координат, |
A |
5; |
|
|
, B |
4; |
|
|
|
– полярные координаты |
|
4 |
12 |
||||||||||
|
|
|
|
|
|
|
|
||||
двух его других вершин.
Задачи повышенного уровня сложности 12
8. В полярной системе координат даны две противоположные верши-
|
6; |
|
7 |
|
4; |
|
. Найти его площадь. |
||
ны квадрата: A |
12 |
|
и C |
6 |
|
||||
|
|
|
|
|
|
|
|
||
9.Полярная система координат совмещена с ПДСК стандартным образом. Найти ГМТ плоскости, координаты которых совпадают в обеих системах координат.
10.Одна из вершин треугольника лежит в полюсе полярной системы
координат, а другие в точках А(2; 0) и |
|
4; |
|
. Найти радиус впи- |
|
B |
3 |
|
|||
|
|
|
|
|
|
санной в треугольник окружности.
11. Полюс полярной системы координат совмещен с вершиной правильного треугольника со стороной 1, а полярный луч направлен по его стороне. Найдите полярные координаты всех вершин треугольника.
Домашнее задание 12. Полярная система координат
1. В ПДСК даны точки: А(0; 1), В(0; –1), С(1; 0), D(–1; 0), Е(1; 1), F(1; –1), G(–1; –1), H(–1; 1), I(1; 3), J( 3;1) . Найдите их полярные ко-
ординаты в полярной системе координат стандартным образом совмещенной с прямоугольной.
2. Вычислить площадь треугольника, вершины которого заданы в по-
лярной системе координат: |
|
3; |
|
, |
|
8; |
7 |
|
6; |
5 |
|||
A |
8 |
|
B |
24 |
|
, C |
8 |
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
3.Полюс полярной системы координат совмещен с центром правильного треугольника со стороной 1, а полярный луч параллелен его стороне. Найдите полярные координаты всех вершин треугольника.
10
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 12, с.13
Самостоятельная работа 12
Вариант 1.
1.Определение полярного радиуса точки в полярной системе координат.
2. Постройте в полярной системе координат точку |
|
2; |
|
|
и найди- |
|
A |
3 |
|
||||
|
|
|
|
|
|
|
те полярные координаты точки, симметричной точке А относительно полюса.
3.Постройте в полярной системе координат треугольник АВС и найдите его угол при вершине А, если его вершины имеют координаты:
|
3; |
|
|
4; |
4 |
||
A(0;0), B |
3 |
|
, C |
3 |
. |
||
|
|
|
|
|
|
||
Вариант 2.
1. Определение полярного угла точки в полярной системе координат.
|
|
|
2 |
|
||
2. Постройте в полярной системе координат точку |
A |
2; |
|
|
и найди- |
|
3 |
||||||
|
|
|
|
|
||
те полярные координаты точки, симметричной точке А относительно полярного луча.
3.Постройте в полярной системе координат треугольник АВС и найдите его угол при вершине А, если его вершины имеют координаты:
|
3; |
|
|
4; |
7 |
||
A(0;0), B |
6 |
|
, C |
6 |
. |
||
|
|
|
|
|
|
||
Вариант 3.
1.Определение полярных координат точки в полярной системе координат.
2.ПДСК совмещена с полярной. Найдите декартовые координаты
точки, заданной полярными координатами |
|
2; |
5 |
. Постройте |
|
A |
3 |
|
|||
|
|
|
|
|
|
чертеж.
3.Найдите площадь треугольника АВС, если его вершины в полярной системе координат имеют координаты:
|
3; |
|
|
4; |
4 |
||
A(0;0), B |
3 |
|
, C |
3 |
. |
||
|
|
|
|
|
|
||
|
11 |
|
|
|
|
|
|
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 12, с.13
Вариант 4.
1.Определение полярной системы координат.
2.ПДСК совмещена с полярной. Найдите полярные координаты точ-
ки, заданной декартовыми координатами A 3; 4 . Постройте
чертеж.
3. Найдите площадь треугольника АВС, если его вершины в полярной
системе координат имеют координаты: |
|
3; |
|
|
4; |
7 |
||
A(0;0), B |
6 |
|
, C |
6 |
. |
|||
|
|
|
|
|
|
|
||
Постройте чертеж.
п.5. Вопросы и задачи для самоконтроля 12 Обозначения
1.Обозначение полярного радиуса точки плоскости.
2.Обозначение полярного угла точки плоскости.
3.Обозначение полярных координат точки плоскости.
Определения
1.Определение полюса и полярного луча.
2.Определение полярного радиуса точки плоскости.
3.Определение полярного угла точки плоскости.
4.Определение полярных координат точки плоскости.
5.Определение полярной системы координат на плоскости.
6.Определение стандартного совмещения полярной системы координат с ПДСК.
7.Определение полярного угла вектора на координатной плоскости.
Теоремы
1.Связь декартовых координат точки с её полярными координатами.
2.Вычисление полярных координат точки по известным её декартовым координатам.
3.Связь полярного угла вектора на координатной плоскости с его направляющими углами.
12

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 12, с.13
Тест 12 |
|
|
|
|
|
|
|
1. |
В полярной системе координат на плоскости постройте точки, за- |
||||||
|
данные |
|
|
|
своими |
полярными |
координатами: |
|
|
|
|
|
5 |
|
|
|
A 2; |
2 |
, B(3; ), C 1; |
. |
|
||
|
|
|
|
|
4 |
|
|
2. |
Определить |
полярные |
координаты точек, |
симметричных точке |
|||
|
|
|
5 |
относительно полюса и полярной оси. |
|||
|
A 3; |
|
|||||
|
|
|
6 |
|
|
|
|
3. |
Постройте на координатной плоскости, точку с полярными коорди- |
||||||
|
натами |
M(4; |
7 |
) и найдите её декартовые координаты. |
|||
|
6 |
||||||
|
|
|
|
|
|
|
|
4.Зная декартовые координаты точки M( 3, 1) , найдите её полярные координаты и укажите их на координатной плоскости.
5.На плоскости дан квадрат со стороной 1 и полярная система координат, в которой полюсом служит центр квадрата, а полярный луч проходит через середину его стороны. Найдите полярные координаты вершин квадрата.
6.На плоскости дан квадрат со стороной 1 и полярная система координат, в которой полюсом служит центр квадрата, а полярный луч проходит через одну из его вершин. Найдите полярные координаты вершин квадрата.
7.На плоскости дан квадрат со стороной 1 и полярная система координат, в которой полюсом служит вершина квадрата, а полярный луч проходит через вершину, противоположную полюсу. Найдите полярные координаты вершин квадрата.
8.На плоскости дан правильный треугольник со стороной 1 и полярная система координат, в которой полюсом служит центр треугольника, а полярный луч проходит параллельно его стороне. Найдите полярные координаты вершин треугольника.
9.На плоскости дан правильный треугольник со стороной 1 и полярная система координат, в которой полюсом служит одна из вершин треугольника, а полярный луч проходит по его стороне. Найдите полярные координаты вершин треугольника.
10.Вычислить площадь треугольника ОАВ, где О – полюс полярной
системы координат, |
|
|
|
|
|
|
|
|
|||
A |
5; |
|
|
, B |
4; |
|
|
|
– полярные координаты |
||
4 |
12 |
||||||||||
|
|
|
|
|
|
|
|
||||
двух его других вершин.
13
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 12, с.14
Практическое занятие 13 Комплексная плоскость
Краткое содержание: комплексная плоскость, модуль и аргумент комплексного числа, тригонометрическая форма записи комплексных чисел, умножение и деление комплексных чисел в тригонометрической форме записи, формула Муавра.
п.1. Теория п.1.1. Комплексная плоскость
Теорема. Между множеством комплексных чисел и множеством точек координатной плоскости существует взаимно однозначное соответствие.
Это соответствие устанавливается правилом:
z x yi C (x, y) R2 .
В силу этого соответствия можно каждое комплексное число z x yi C отождествить с точкой координатной плоскости Оху,
которая имеет координаты (х, у).
Определение. Координатная плоскость, каждая точка которой отождествлена с комплексным числом, называется комплексной плоскостью. Ось абсцисс Ох, в этом случае, называется действительной осью, ось ординат Оу – мнимой осью.
|
у |
|
|
|
z a bi |
b |
r |
|
|
|
х
Оа
Рис. 1
Замечание. Существует взаимно однозначное соответствие между точками координатной плоскости и их радиус-векторами. Поэтому также существует взаимно однозначное соответствие и между всеми комплексными числами и радиус-векторами соответствующих точек комплексной плоскости. В силу этого соответствия, можно графически изображать комплексные числа радиус-вектором соответствующей точки на комплексной плоскости. (Смотрите рисунок 1.)
1
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 12, с.14
Итак, чтобы изобразить комплексное число z точкой на комплексной плоскости нужно записать его в алгебраической форме записи, и построить в ПДСК на этой плоскости точку, абсцисса которой равна действительной части, а ордината – мнимой части данного комплексного числа z.
п.1.2. Модуль и аргумент комплексного числа
Введем на комплексной плоскости полярную систему координат стандартным образом совмещенную с ПДСК, т.е. с полюсом в начале координат и полярным лучом, совмещенным с положительной полуосью абсцисс. Тогда точка z имеет полярные координаты (r, ) , где r –
полярный радиус точки z, а – ее полярный угол. (Рисунок 1.)
Определение. Модулем комплексного числа называется полярный радиус точки комплексной плоскости отождествленной с этим числом, и обозначается | z | r .
Определение. Аргументом комплексного числа называется полярный угол точки комплексной плоскости отождествленной с этим числом, и обозначается arg z .
Таким образом, полярные координаты точки z комплексной плоскости называются модулем и аргументом комплексного числа z.
Из определений следует, что | z | [0; ) , arg z [0; 2 ) или arg z ( ; ].
Можно дать следующее определение модуля комплексного числа совпадающее с первым.
Определение. Модулем комплексного числа называется расстояние от начала координат комплексной плоскости до точки, отождествленной с этим числом.
п.1.3. Тригонометрическая форма записи комплексного числа Теорема. Пусть точка z комплексной плоскости имеет декартовые координаты (х, у), т.е. z x yi и полярные (r, ) , тогда они связаны
соотношением:
2

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 12, с.14
x r cosy r sin .
По определению, r | z |, arg z и, подставляя в алгебраическую форму записи числа z, получаем:
zx yi | z | cos(arg z) i | z | sin (arg z)| z | (cos(arg z) isin (arg z)).
Определение. Запись комплексного числа в виде z | z | (cos(arg z) isin (arg z))
называется его тригонометрической формой.
Замечание. Поскольку одну букву писать экономнее нежели несколько, то чаще всего тригонометрическую форму комплексного числа пишут в виде:
z | z | (cos isin ) ,
где arg z .
Теорема. (О равенстве комплексных чисел в тригонометрической форме.)
Два комплексных числа равны тогда и только тогда, когда равны их модули и аргументы.
Используя соотношения, которые связывают полярные и декартовые координаты точки плоскости, можно найти модуль и аргумент комплексного числа зная его действительную и мнимую части.
Теорема. Пусть z x yi , т.е. x Rez, y Im z . Тогда
| z | |
x2 y2 , |
arg z arctg |
y |
, |
|
x |
|||||
|
|
|
|
если точка z лежит в первой или четвертой четверти или arg z arctg xy ,
если точка z лежит во второй или третьей четверти.
Замечания. Если полярный угол лежит в первой или четвертой чет-
3
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 12, с.14
верти: 2 ; 2 , то его можно выразить через арксинус:
sin |
y |
|
|
y |
|
и arcsin |
|
|
y |
. |
|
|
|
|
|
||||
|
|
|
x2 y2 |
|
|
x2 y2 |
|
|
|
|
|||||||||
|
|
r |
|
|
|
|
|
|
|
|
|
|
|||||||
Если полярный угол лежит в первой или второй четверти: |
[0; ] , |
||||||||||||||||||
то его можно выразить через арккосинус: |
|
|
|
|
|
|
|
|
|||||||||||
cos |
x |
|
|
x |
|
и arccos |
|
y |
|
. |
|
|
|
|
|||||
|
|
x2 y2 |
|
x2 y2 |
|
|
|
|
|
||||||||||
|
|
r |
|
|
|
|
|
|
|
|
|
|
|||||||
Если же если полярный угол лежит в третьей четверти: |
|
|
|
|
3 |
, то |
|||||||||||||
|
; |
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arcsin |
y |
2 arccos |
x |
|
|
. |
|
|
|
|
|||||||||
x2 y2 |
x2 y2 |
|
|
|
|
||||||||||||||
В некоторых случаях удобнее не пользоваться формулами, а изображать на чертеже соответствующую точку на комплексной плоскости и находить модуль и аргумент комплексного числа пользуясь чертежом. Смотрите ниже примеры.
Несмотря на то, что cos( ) cos , а sin ( ) sin , форма за-
писи комплексного |
числа |
z с аргументом arg z в |
виде |
|
z | z | (cos isin ) |
не |
является |
тригонометрической, |
т.к. |
arg z . В этом случае правильной записью тригонометриче-
ской формы комплексного числа будет:
z | z | (cos( ) isin ( ))
или
z | z | (cos(2 ) isin (2 )) .
Теорема. (Об умножении комплексных чисел в тригонометрической форме записи.) Пусть
z1 | z1 | (cos 1 isin 1 ) , z2 | z2 | (cos 2 isin 2 )
где 1 arg z1 и 2 arg z2 – два произвольных комплексных числа
записанных в тригонометрической форме. Тогда
z1z2 | z1 | | z2 | (cos( 1 2 ) isin ( 1 2 )) .
Следствие 1. Пусть k натуральное число и k {1, 2, ..., n} . Пусть далее
4

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 12, с.14
zk | zk | (cos k isin k ) , где k arg zk – произвольные n комплекс-
ных чисел записанных в тригонометрической форме записи. Тогда z1 z2 ... zn | z1 | | z2 | ... | zn | (cos( 1 2 ... n )
isin ( 1 2 ... n )) .
Следствие 2. Пусть n натуральное число и z | z | (cos isin ) – про-
извольное комплексное число в тригонометрической форме записи. Тогда
zn | z |n (cos n isin n ) .
Можно сформулировать следующее правило умножения комплексных чисел в тригонометрической форме записи.
Правило умножение комплексных чисел
При умножении комплексных чисел их модули перемножаются, а аргументы складываются.
Теорема. (Свойства модуля комплексного числа.) Пусть z, z1 ,z2 C –
произвольные комплексные числа и соответствующие точки на комплексной плоскости. Тогда:
1) | z1 z2 | | z1 | | z2 | и | z | | z |.
Т.е. модуль произведения комплексных чисел равен произведению их модулей и модули противоположных чисел равны;
2)расстояние между точками z1 и z2 комплексной плоскости равно модулю разности соответствующих комплексных чисел: | z1 z2 |;
3)| z1 z2 | | z1 | | z2 | ; (неравенство треугольника)
4)| z1 z2 | | z1 | | z2 | .
Теорема. (Формула Муавра.) Для любого целого числа n и любого действительного числа имеет место следующее равенство:
(cos isin )n cos(n ) isin (n ) .
Следствие. (О целых степенях комплексного числа.) Пусть z | z | (cos isin ) . Тогда n Z
5
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 12, с.14
zn | z |n (cos(n ) isin (n )) .
Теорема. (О делении комплексных чисел в тригонометрической форме) Пусть
z1 | z1 | (cos 1 isin 1 ) , z2 | z2 | (cos 2 isin 2 )
где 1 arg z1 и 2 arg z2 – два произвольных комплексных числа
записанных в тригонометрической форме. Тогда |
|
|
|||||||
|
z1 |
|
| z1 |
| |
(cos( |
2 |
) isin ( |
2 |
)) . |
|
|
|
|
||||||
|
z2 |
| z2 |
| |
1 |
1 |
|
|||
|
|
|
|
|
|
||||
Правило деления комплексных чисел
При делении комплексных чисел их модули делятся, а аргументы вычитаются.
п.2. Список задач Список №1
1.Построить комплексное число, заданное в алгебраической форме, на комплексной плоскости, найти его модуль, аргумент, и записать в тригонометрической форме.
2.Построить на комплексной плоскости комплексное число, комплексно сопряженное данному, найти его модуль, аргумент, и записать в тригонометрической форме.
3.Записать в алгебраической форме комплексное число, заданное в тригонометрической форме.
4.Найти произведение и частное двух комплексных чисел, заданных в тригонометрической форме.
5.Найти целую степень комплексного числа, заданного в тригонометрической форме.
6.Найти расстояние между двумя точками на комплексной плоскости.
7.Изобразить на комплексной плоскости все точки, удаленные от данной на заданное расстояние.
8.Изобразить на комплексной плоскости все комплексные числа, имеющие заданный аргумент.
Список №2
1.Изобразить множество точек комплексной плоскости, удовлетворяющих заданным условиям.
6
