АГ ПЗ 1-35 (полный вариант)

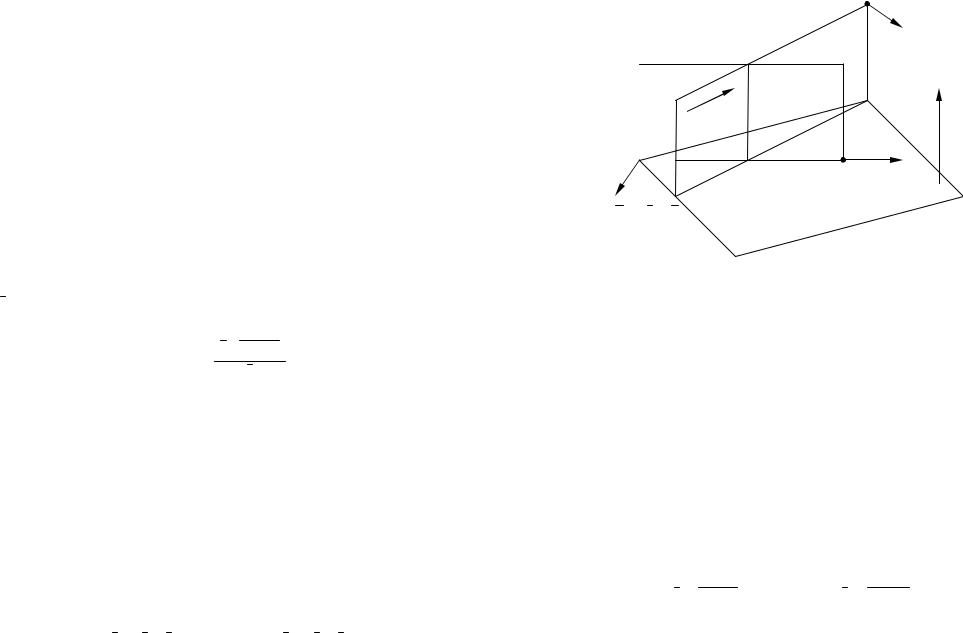
Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 23, с.22

чением взаимно перпендикулярных плоскостей и , причем последняя перпендикулярна прямой L. Обе они проходят через точку M1 , а их нормальные векторы изображены на рисунке.

Замечание. Из определения следует, что точка M2 на рисунке 2 является проекцией точки M1 на прямую L, а длина перпендикуляра M1M2 равна расстоянию от точки M1 до прямой L.

s (m,n,p) – координаты направляющего вектора данной прямой. Длину перпендикуляра можно найти по формуле:

d | s Mo M1 | . | s |

Определение. Общим перпендикуляром двух скрещивающихся прямых называется прямая, пересекающая каждую из них под прямым углом.

Теорема. Уравнение общего перпендикуляра двух скрещивающихся

имеет вид:

A1 (x x1 ) B1 (y y1 ) C1 (z z1 ) 0 ,

A2 (x x2 ) B2 (y y2 ) C2 (z z2 ) 0 где (A1 ,B1 ,C1 ) s1 (s1 s2 ), (A2 ,B2 ,C2 ) s2 (s1 s2 ) .

7

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 23, с.22

n s1 n

Рис. 3

Пояснения к рисунку 3. Сначала через прямую L1 проводится плоскость параллельно прямой L2 . Плоскость проводится через прямую L1 перпендикулярно плоскости . Плоскость проводится через прямую L2 перпендикулярно плоскости . Тогда их пересечение есть общий перпендикуляр р.

Теорема. Уравнение прямой, проходящей через точку Mo (xo , yo ,zo ) , и пересекающей две скрещивающиеся прямые

имеет вид:

A1 (x xo ) B1 (y yo ) C1 (z zo ) 0 ,

A2 (x xo ) B2 (y yo ) C2 (z zo ) 0 где (A1 ,B1 ,C1 ) s1 Mo M1 , (A2 ,B2 ,C2 ) s2 Mo M2 .

8

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 23, с.22

L2

s2

M2

L1

s1

Рис. 4

Пояснение к рисунку 4. Плоскость проводится через точку Mo и прямую L1 . Плоскость проводится через точку Mo и прямую L2 .

Их нормальные векторы указаны на рисунке. Искомая прямая является линией пересечения построенных плоскостей и .

п.2. Список задач Список №1

1.Найти каноническое и параметрическое уравнения прямой, проходящей через данную точку, и параллельную данному вектору или данной прямой.

2.Найти параметрическое уравнение прямой, зная её каноническое уравнение, и наоборот.

3.Найти каноническое уравнение прямой, проходящей через две данные точки.

4.Зная каноническое уравнение прямой, задать прямую пересечением

9

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 23, с.22

двух плоскостей.

5.Найти каноническое уравнение прямой, заданной пересечением двух плоскостей.

6.Найти угол между двумя прямыми.

7.Определить взаимное расположение двух пространственных прямых.

8.Найти точку пересечения двух пересекающихся пространственных прямых.

Список №2

1.Найти расстояние между двумя параллельными прямыми в пространстве.

2.Найти расстояние от точки до прямой.

3.Найти расстояние между двумя скрещивающимися прямыми.

4.Составить уравнение перпендикуляра, опущенного из данной точки на данную пространственную прямую.

5.Найти проекцию точки на прямую.

6.Найти каноническое уравнение общего перпендикуляра, проведенного к двум скрещивающимся прямым.

7.Найти уравнение прямой, проходящей через данную точку, и пересекающую две данные скрещивающиеся прямые.

п.3. Примеры Пример 1. Найти каноническое и параметрическое уравнения прямой,

проходящей через точку М(–2; 4; 0), если вектор s (1, 0, 3) является

её направляющим вектором.

Решение. Подставляем в каноническое уравнение прямой

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 23, с.22

Пример 2. Найти параметрическое уравнение прямой

Решение. Из параметрического уравнения прямой сразу же находим координаты точки, лежащей на этой прямой. Их можно найти, положив t 0 : (xo , yo ,zo ) ( 5; 1;2) . Коэффициенты при параметре t да-

ют соответствующие координаты направляющего вектора этой прямой: s ( 1;0;1) . Составляем каноническое уравнение данной прямой.

Ответ: x 5 y 1 z 2 .1 0 1

Замечание. Каноническое уравнение можно получить, если из каждо-

го уравнения системы выразить параметр t: t x 5 x 5 ,

1

11

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 23, с.22

t z 2 z 1 2 . Второе уравнение запишем в виде:

y 1 0 t t y0 1 ,

где последнее равенство нужно понимать формально, как картинку, а не как действие деления. Приравнивая правые части полученных равенств, получаем ответ.

Пример 4. Найти каноническое уравнение прямой, проходящей через точки А(–1; 2; –5) и В(2; 6; 7).

Решение. Воспользуемся каноническим уравнением прямой, проходящей через две данные точки:

Подставляем в это уравнение координаты точек А и В:

Пример 5. Найти точку пересечения двух пересекающихся пространственных прямых

Выражаем t из первого уравнения и подставляем во второе и третье уравнения:

12

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 23, с.22

– система имеет единственное решение, следовательно, прямые пересекаются. Подставляем найденные значения t и k в параметрические уравнения прямых и находим координаты общей точки.

Ответ: (– 6; 9; – 4).

плоскостей.

Решение. Записываем каноническое уравнение прямой в виде системы:

Пример 7. Определить взаимное расположение двух пространственных прямых

Решение. Из канонического уравнения 1-й прямой находим координаты точки, лежащей на ней и координаты её направляющего вектора:

щиеся. Вычислим смешанное произведение векторов

13

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 23, с.22

Ответ: прямые скрещивающиеся.

Пример 8. Найти каноническое уравнение прямой, заданной пересечением плоскостей:

x 2y z 1 0 L : 2x y 2z 3 0 .

Решение. Найдем координаты какой-нибудь точки, лежащей на данной прямой. Исключим из уравнения одно из переменных. Умножим, например, первое уравнение на 2 и сложим оба уравнения. Получаем 4x 3y 1 0 . Положим в этом уравнении y 3 . Получаем x 2 .

Подставляя найденные значения х и у в первое уравнение, находим z 5 . Таким образом, точка с координатами ( 2;3;5) лежит на дан-

ной прямой, т.е. xo 2, yo 3, zo 5 . Найдем ее направляющий век-

тор. Выписываем нормальные векторы данных плоскостей и вычисляем их векторное произведение:

эти числа в каноническое уравнения, получаем ответ.

Отсюда следует, что прямые либо совпадают, либо параллельные. Пусть

14

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 23, с.22

s (3; 2; 2)

– их общий направляющий вектор. Из канонических уравнений прямых находим, что точки

M1 (0;1; 1) L1 , M2 (2; 0; 0) L2 .

Находим координаты вектора

M1M2 (2; 1;1) .

Видим, что M1M2 || s , т.е. данные прямые не совпадают, а параллельные. Вычисляем векторное произведение

и его модуль

| s M1M2 | 2 .

Вычисляем модуль направляющего вектора и искомое расстояние между данными параллельными прямыми:

L2 : x y z 1 скрещивающиеся, и найти расстояние между ними. Решение. Находим координаты точек, лежащих на данных прямых

вывод, что данные прямые скрещивающиеся. Вычисляем векторное

смешанного и векторного произведения векторов, подставляем в фор15

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 23, с.22

мулу расстояния между скрещивающимися прямыми:

Ответ: 2 14 . 7

Пример 11. Найти уравнение перпендикуляра, опущенного из точки А(1; 1; 1) на прямую x 2y 2z , и координаты проекции точки А на

эту прямую.

Решение. Воспользуемся теоремой пункта 6. Искомый перпендикуляр является прямой пересечения двух плоскостей, одна из которых проводится через точку А и данную прямую, другая проводится через точку А перпендикулярно данной прямой. Смотрите рисунок 2. Уравнение искомой прямой имеет вид:

динат, это точка лежащая на данной прямой. Запишем данную прямую в каноническом виде:

x2 y z .

Отсюда находим координаты её направляющего вектора:

Теперь мы можем записать уравнение искомого перпендикуляра:

Отсюда находим каноническое и параметрическое уравнение перпендикуляра:

16

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 23, с.22

Теперь найдем точку пересечения В этого перпендикуляра и данной прямой. Точка В и будет проекцией точки А на данную прямую. Запишем данное уравнение в параметрической форме и воспользуемся теоремой пункта 3:

x 2k

y k .z k

Решаем систему:

вующее параметрическое уравнение, находим координаты проекции точки А на данную прямую:

B 4 ; 2 ; 2 .3 3 3

п.4. Задачи Задачи для аудиторного решения 23

1. Составить уравнение прямой, проходящей через точку М(2; 0; –3), и

2.Составить уравнение движения точки, которая двигается прямолинейно и равномерно из точки М(3; –1; –5) в направление вектора

17

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 23, с.22

s ( 2; 6; 3) со скоростью v 21.

3. Найдите параметрическое уравнение прямой:

4. Найдите каноническое уравнение прямой:

5.Составить каноническое и параметрическое уравнения прямой, про-

ходящей через точки: а) (1; –2; 1), (3; 1; –1); б) (3; 1; 0), (1; 0; –3).

6.Найдите острый угол между прямыми:

Задачи повышенного уровня сложности 23

13. Найти расстояние между скрещивающимися прямыми

18

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 23, с.22

x 2t 4, y t 4, z 2t 1, x 4t 5, y 3t 5, z 5t 5.

15.Найдите уравнение перпендикуляра, опущенного из точки А(2; –2;

1)на прямую x 2t 1, y 3t 2 , z 2t 3 .

16.Найдите уравнение прямой, проходящей через точку А(–4; –5; 3),

17. Найдите параметрическое уравнение общего перпендикуляра пря-

мых x 3t 7, y 4 2t, z 3t 4 и x 1 t, y 2t 8, z t 12 .

Домашнее задание 23. Уравнение прямой в пространстве

1.Даны вершины треугольника А(3; 6; –7), В(–5; 2; 3) и С(4; –7; –2). Составить каноническое и параметрическое уравнения его медианы, проведенной из вершины С. Задайте найденное уравнение медианы пересечением плоскостей.

2.Выясните взаимное расположение двух данных прямых. Если они пересекаются, найдите координаты точки пересечения; если параллельные или скрещивающиеся – найдите расстояние между ними:

Самостоятельная работа 23

Вариант 1.

1.Определение канонического уравнения прямой в координатном пространстве Oxyz.

2.Найдите параметрическое уравнение прямой, проходящей через

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 23, с.22

Вариант 2.

1.Определение параметрического уравнения прямой в координатном пространстве Oxyz.

2.Найдите каноническое уравнение прямой, проходящей через точки А(4; –7; –2) и В(–5; 2; 3).

1.Определение уравнения линии в координатном пространстве Oxyz.

2.Через вершину С(4; –7; –2) треугольника АВС проведите прямую (найдите её уравнение), параллельную стороне АВ, если А(3; 6; –7),

В(–5; 2; 3).

3.Найдите каноническое уравнение прямой x 1 t, y 9t, z 1.

Вариант 4.

1.Определение параметрического уравнения линии в координатном пространстве Охуz.

2.Через вершину А(3; 6; –7) треугольника АВС проведите прямую (найдите её уравнение), параллельную стороне ВС, если В(–5; 2; 3),

С(4; –7; –2).

3.Найдите уравнение перпендикуляра, проведенного из точки А(1; 2;

3)к оси Ох.

п.5. Вопросы и задачи для самоконтроля 23 Обозначения

1.Обозначение направляющего вектора прямой в пространстве.

2.Обозначение расстояния между двумя параллельными или скрещивающимися прямыми.

Определения

1.Определение уравнения линии в пространстве.

2.Определение параметрического уравнения линии в пространстве.

3.Определение направляющего вектора прямой.

4.Определение параметрического уравнения прямой в пространстве.

5.Определение канонического уравнения прямой в пространстве.

6.Определение уравнения прямой, проходящей через две точки.

7.Определение перпендикуляра, проведенного из данной точки на данную прямую.

8.Определение длины перпендикуляра, проведенного из данной точ-

20

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 23, с.22

ки на данную прямую.

9.Определение общего перпендикуляра двух скрещивающихся прямых.

Теоремы

1.Параметрическое уравнение прямой в пространстве.

2.Каноническое уравнение прямой в пространстве.

3.Взаимное расположение двух прямых в пространстве, заданных каноническими уравнениями.

4.Взаимное расположение двух прямых в пространстве, заданных параметрическими уравнениями.

5.Формула расстояния между двумя параллельными прямыми.

6.Формула расстояния между двумя скрещивающимися прямыми.

7.Прямая в пространстве, как результат пересечения двух плоскостей.

8.Приведение канонического уравнения прямой к уравнению прямой, заданной пересечением двух плоскостей.

9.Уравнение перпендикуляра, проведенного из данной точки на данную прямую.

10.Теорема об уравнении общего перпендикуляра двух скрещивающихся прямых.

11.Уравнение прямой, проходящей через данную точку, и пересекающая две данные прямые.

Тест 23

1.Составить каноническое уравнение прямой, проходящей через точку М(2; 0; –3), и параллельной вектору a (2; 3; 5) .

2.Составить каноническое уравнение прямой, проходящей через точку М(0; 0; 3), и параллельной оси Ох.

3.Составить каноническое уравнение прямой, проходящей через точ-

6.Составить каноническое уравнение прямой, проходящей через точ-

ки А(1; –2; 1) и В(3; 1; –1).

21

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 23, с.22

22

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 24, с.21

Практическое занятие 24 Прямая в пространстве и плоскость

Теорминимум: взаимное расположение прямой в пространстве и плоскости, угол между прямой и плоскостью, точка встречи прямой с плоскостью, проекция точки на плоскость, проекция точки на прямую, расстояние между параллельными прямой и плоскостью, связка и пучок плоскостей, решение основных задач на прямую в пространстве и плоскость.

п.1. Теория п.1.1. Связка и пучок плоскостей

Определение. Связкой плоскостей называется множество всех плоскостей, имеющих одну общую точку, которая называется центром связки.

Теорема. Пусть 1 : A1x B1y C1z D1 0 ,

2 : A2 x B2 y C2 z D2 0 , 3 : A3 x B3 y C3z D3 0

–три плоскости в ПДСК Охуz, имеющие единственную общую точку

Mo . Тогда уравнение

(A1x B1y C1z D1 ) (A2 x B2 y C2 z D2 )(A3x B3 y C3z D3 ) 0 ,

где , , R – произвольные действительные параметры одновременно не равные нулю, есть уравнение связки плоскостей с центром связки в точке Mo .

Теорема. Уравнение

A(x xo ) B(y yo ) C(z zo ) 0 ,

где А, В и С произвольные действительные параметры, одновременно не равные нулю, является уравнением связки плоскостей с центром связки в точке Mo (xo , yo ,zo ) .

Определение. Пучком плоскостей называется множество всех плоскостей пересекающихся по одной и той же прямой, называемой осью пучка.

Теорема. Пусть

1 : A1x B1y C1z D1 0 и 2 : A2 x B2 y C2 z D2 0

1

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 24, с.21

– две плоскости, пересекающиеся по прямой L. Тогда уравнение

(A1x B1y C1z D1 ) (A2 x B2 y C2 z D2 ) 0 ,

где , R – произвольные действительные параметры одновременно не равные нулю, есть уравнение пучка плоскостей с осью пучка L.

произвольной прямой в пространстве, и пусть m 0 . Тогда уравнение

является уравнением пучка плоскостей, осью которого является данная прямая L.

п.1.2. Взаимное расположение 3-х плоскостей

Возможны следующие случаи взаимного расположения трех плоскостей в пространстве:

1)все три плоскости совпадают;

2)две плоскости совпадают, а третья параллельна им;

3)две плоскости совпадают, а третья не параллельна им;

4)все три плоскости параллельны друг другу;

5)две плоскости параллельные, а третья пересекает их;

6)все три плоскости пересекаются по одной прямой, т.е. находятся в одном пучке плоскостей;

7)все три плоскости попарно пересекаются по трем параллельным прямым (случай треугольной «трубы»);

8)все три плоскости пересекаются в одной точке.

Теорема. Пусть даны общие уравнения трех плоскостей:

1 : A1x B1 y C1z D1 0 , 2 : A2 x B2 y C2 z D2 0 ,

3 : A3 x B3 y C3 z D3 0 , ni (Ai ; Bi ;Ci ), i 1, 2,3 – их соответст-

вующие нормальные векторы. Тогда:

1) если n1 || n2 || n3 , то все три плоскости совпадают или попарно па-

раллельные, или две из них совпадают, а третья параллельна им (в этом случае определяется взаимное расположение каждой пары плоскостей по отдельности);

2) если среди трех нормальных векторов n1 , n2 , n3 имеются ровно два

2

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 24, с.21

коллинеарных, то две плоскости пересекаются, а третья либо совпадает с одной из них, либо параллельна одной из них (в этом случае также по отдельности определяется взаимное расположение каждой пары плоскостей);

3) если среди трех нормальных векторов n1 , n2 , n3 нет коллинеарных,

аих смешанное произведение равно нулю, n1 n2 n3 0 , то плоскости пересекаются либо по одной прямой, и в этом случае система уравнений

A1x B1y C1z D1 0A2 x B2 y C2 z D2 0

является уравнением этой прямой, либо плоскости пересекаются по трем параллельным прямым (образуя треугольную «трубу»), и в этом случае система

A x B y C z D 0

1 1 1 1

A2 x B2 y C2 z D2 0A3 x B3 y C3 z D3 0

не имеет решений; 4) если смешанное произведение нормальных векторов не равно нулю

n1 n2 n3 0 , то плоскости пересекаются в одной точке, координаты которой являются единственным решением последней системы из трех уравнений.

п.1.3. Взаимное расположение прямой в пространстве и плоскости

Возможны три случая взаимного расположения прямой в пространстве и плоскости:

1)прямая лежит на плоскости;

2)прямая параллельна плоскости;

3)прямая пересекает плоскость в некоторой точке.

Определение. Точка пересечения прямой и плоскости называется точкой встречи прямой с плоскостью.

Теорема. Пусть плоскость задана общим уравнением

: Ax By Cz D 0 ,

апрямая L задана каноническим или параметрическим уравнениями

3

Головизин В.В. ПЗ по курсу «Алгебра и геометрия», УдГУ, Ижевск – 2010, ПЗ 24, с.21

вкоторых n (A, B, C) – координаты нормального вектора плоскости

, Mo (xo , yo , zo ) – координаты произвольной фиксированной точки

прямой L, s (m, n, p) – координаты её направляющего вектора. Тогда:

1) если n s Am Bn Cp 0 , то прямая L пересекает плоскость в точке, координаты которой можно найти из системы уравнений

Следствие. Если система (1) имеет единственное решение, то прямая пересекается с плоскостью; если система (1) не имеет решений, то прямая параллельная плоскости; если система (1) имеет бесконечно много решений, то прямая лежит на плоскости.

п.2. Список задач Список №1

1.Определить взаимное расположение прямой и плоскости.

2.Найти угол между прямой и плоскостью.

3.Найти точку встречи прямой с плоскостью.

4.Найти точки пересечения данной плоскости с координатными осями.

5.Найти каноническое уравнение прямой, проходящей через данную точку, и перпендикулярной данной плоскости.

6.Найти проекцию точки на плоскость.

7.Найти общее уравнение плоскости, проходящей через данную точ-

4