4. Моделирование системы управления нелинейного объекта с использованием линейных типовых регуляторов (пи-закон регулирования)

В большинстве случаев промышленные объекты, в том числе и рассматриваемый тип реактора, являются многомерными. Их состояние характеризуется несколькими величинами, значения которых определяются значениями входных переменных (ряд этих переменных являются возмущениями, другая часть может выступать в качестве регулирующих воздействий). Из всей совокупности переменных состояния измерению, контролю и регулированию подлежит только определенная часть. Эти переменные называются выходными. Регулирование многомерных объектов может быть НЕСВЯЗАННЫМ и СВЯЗАННЫМ. В первом случае каждая выходная переменная регулируется одним регулятором, воздействующим только на «свой» регулирующий орган; во втором случае каждый регулятор воздействует не только на свой регулирующий орган, но и на регулирующие органы других регулируемых величин.

Рис. 4. Функциональная схема автоматизации

Рис. 5. Структурная схема системы несвязного регулирования многомерного одноконтурного объекта.

4.1 Оценка параметров настроек регулятора

Поскольку объект по каналам регулирования характеризуется малым запаздыванием и является устойчивым, то целесообразно использовать ПИ-алгоритм регулирования:

.

При решении задач моделирования систем управления на ЭВМ необходимо иметь математическое описание объекта и регулятора, представленных в одинаковой форме – в виде обыкновенных дифференциальных уравнений. Преобразуем уравнение для регулятора в дифференциальную форму:

,

где - значение регулирующего воздействия в статике. Подставляя в данное уравнение значение ошибки регулирования из уравнения сумматора, получим уравнения работы регуляторов:

Найдем настройки регулятора по методу Циглера-Никольса для канала :

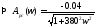
Построим фазочастотную характеристику:

Рис. 15. Фазочастотная характеристика.

Определим настройки ПИ-регулятора:

Аналогично найдем настройки для канала :

Получили:

Настройки регулятора уровня примем такими же, как и регулятора концентрации вещества А.

5. Моделирование системы управления линеаризованного объекта с использованием аппроксимирующей модели

Проведем моделирование линеаризованной системы в окрестности рабочей точки. Для этого примем передаточные функции, полученные при идентификации объекта управления и настройки регулятора, полученные при оценке параметров настроек регулятора.

Передаточная функция по каналу управления расход разбавителя – концентрация в реакторе имеет вид: W1(p)=k/(Tp+1)=-0.04/(380p+1), по каналу управления расход хладагента – температура в реакторе имеет вид: W2(p)=k/(Tp+1)=-7.29/(600p+1), по каналу управления расход на выходе из реактора – уровень в реакторе имеет вид: W3(p)=k/p=0.000036/p .

Моделирование возможно только по каналам управления, так как по каналам возмущения нет передаточных функций.

Моделирование проведем в среде MatLAB.

Рис. 16. Схема моделирования

Получим результаты моделирования, и оценим параметры качества регулирования:

Примем 50%-е изменение задания регулятору.

1. Процесс регулирования концентрации вещества B при изменении задания регулятору (CА= 0.112 моль/литр, Δ CА =0.056 моль/литр).

Рис. 17. Процесс регулирования концентрации вещества А при изменении задания регулятору (CА= 0.112 моль/литр, Δ CА =0.056 моль/литр).

Динамическая ошибка σ = 0.89%, время регулирования τр=600 мин.

2. Процесс регулирования концентрации вещества B при изменении задания регулятору (CА= 0.112 моль/литр, Δ CА =–0.056 моль/литр).

Рис.18. Процесс регулирования концентрации вещества А при изменении задания регулятору (CА= 0.112 моль/литр, Δ CА =–0.056 моль/литр).

Динамическая ошибка σ = 1.56%, Время регулирования τр=850 мин.

3. Процесс регулирования температуры в ректоре при изменении задания регулятору (t0=82.7790С, Δt0= 41.389 °C)

Рис.19. Процесс регулирования температуры в ректоре при изменении задания регулятору (t0=82.7790С, Δt0= 41.389 °C).

Динамическая ошибка σ = 0.76%, Время регулирования τр=1000 мин.

4. Процесс регулирования температуры в ректоре при изменении задания регулятору (t0=82.7790С, Δt0= -41.389 °C)

Рис.20. Процесс регулирования температуры в ректоре при изменении задания регулятору (t0=82.7790С, Δt0= -41.389 °C).

Динамическая ошибка σ = 21.89%, Время регулирования τр=1200 мин.

5. Процесс регулирования уровня в ректоре при изменении задания регулятору (L=0.889 м, ΔL= 0.4445 м)

Рис.21. Процесс регулирования уровня в ректоре при изменении задания регулятору (L=0.889 м, ΔL= 0.4445 м).

Динамическая ошибка σ = 11.15%, Время регулирования τр=1620 мин.

6. Процесс регулирования уровня в ректоре при изменении задания регулятору (L=0.889 м, ΔL=- 0.4445 м)

Рис.22. Процесс регулирования уровня в ректоре при изменении задания регулятору (L=0.889 м, ΔL= -0.4445 м).

Анализ переходных процессов показывает, что при 50%-х возмущениях выбранные настройки параметров регулятора обеспечивают удовлетворительное качество регулирования.