3. Оптимизация режима работы аппарата

В реакторе осуществляется экзотермическая реакция последовательного типа. Пусть целевым условием эффективности максимизации является степень превращения вещества А: . Поставим задачу оптимизации: при заданном составе исходного сырья и температурной зависимости констант скоростей определить среднее время пребывания и температуру в аппарате, обеспечивающие максимум степени превращения вещества А. Ввиду того, что нагрузка на аппарат задана (и), время пребывания определяется рабочим объемом аппарата –Vp. Аппарат работает в политропическом режиме, поэтому необходимо найти только оптимальный объем аппарата. В математической форме задача имеет вид:

, где ;

–степень превращения вещества А, Vp*, t* - оптимальное значение объема аппарата и температуры. В результате оптимизации варьировался объем аппарата в диапазоне 2001000 литров и температура в диапазоне 40900С. В качестве оптимальных значений варьируемых переменных выбраны значения:Vp=550 литров, t=82.7790С, которые обеспечивают

Решим эту задачу с помощью метода покоординатного спуска. Листинг программы приведен ниже.

Листинг программы моделирования вывода аппарата на статический режим

Аппарат работает в политропическом режиме, реакция - экзотермическая (хладагент жидкость)

1.Исходные данные:

теплоёмкость вещества, кдж/кгградК

теплоёмкость хладагента, кдж/кг градК

плотность вещества в аппарате и входных потоках, кг/л

плотность хладагента, кг/л

коэффициент теплопередачи, кдж / м мин градК

тепловой эффект реакции, кдж/моль

универсальная газовая постоянная, дж/моль градК

концентрация компонента А на входе, моль/л

расход на выходе из реактора V, л/мин

расход на входе в реактор V2, л/мин

расход на входе в реактор V1, л/мин

расход хладагента, л/мин

температура на входе в реактор t1, градС

температура на входе в реактор t2, градС

температура хладагента на входе, градС

2. Постоянные коэффициенты

3. Константа скорости

4. Вектор-функция правых частей дифференциальных уравнений модели

5. Начальные условия и условия интегрирования

6. Решение дифференциальных уравнений модели

концентрация компонента А

Vp*=550 объем реактора

степень превращения по Ca

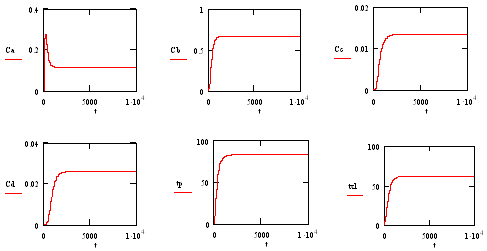
Рис. 3. Процесс вывода аппарата на статический режим

а) изменение концентрации компонента А

б) изменение концентрации компонента В

в) изменение концентрации компонента С

г) изменение концентрации компонента D

д) изменение температуры в реакторе

е) изменение температуры хладагента

При значении величины объема реактора Vp*=550 литров, оптимальное значение температуры t* = 82.7790C

Приняв полученные значения параметров, полученных в ходе оптимизации, в качестве начальных условий системы уравнений (Листинг 1), получили кривые разгона в виде прямых линий, таким образом, убедились, что оптимизация проведена корректно.

Рис 3. Процесс вывода аппарата на статический режим

а) изменение концентрации компонента А

б) изменение концентрации компонента В

в) изменение концентрации компонента С

г) изменение концентрации компонента D

д) изменение температуры в реакторе

е) изменение температуры хладагента