
Несобственные интегралы I рода
Пусть ![]() определена
и непрерывна на множестве от
определена
и непрерывна на множестве от ![]() и
и ![]() .
Тогда:
.
Тогда:
Если
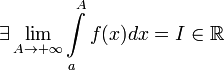 ,
то используется обозначение
,
то используется обозначение 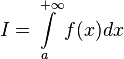 и
интеграл называется несобственным
интегралом Римана первого рода.
В этом случае
и
интеграл называется несобственным
интегралом Римана первого рода.
В этом случае  называется
сходящимся.
называется
сходящимся.Если не существует конечного
 (
( или
или  ),
то интеграл
),
то интеграл  называется
расходящимся к
называется
расходящимся к  ,
или просто расходящимся.
,
или просто расходящимся.
Пусть ![]() определена
и непрерывна на множестве от
определена
и непрерывна на множестве от ![]() и
и ![]() .
Тогда:
.
Тогда:
Если
 ,
то используется обозначение
,
то используется обозначение  и
интеграл называется несобственным
интегралом Римана первого рода.
В этом случае
и
интеграл называется несобственным
интегралом Римана первого рода.
В этом случае  называется
сходящимся.
называется
сходящимся.Если не существует конечного
 (
(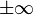 или
или  ),
то интеграл
),
то интеграл  называется
расходящимся к
называется
расходящимся к 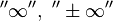 ,
или просто расходящимся.
,
или просто расходящимся.
Если
функция ![]() определена
и непрерывна на всей числовой прямой,
то может существовать несобственный
интеграл данной функции с двумя
бесконечными пределами интегрирования,
определяющийся формулой:
определена
и непрерывна на всей числовой прямой,
то может существовать несобственный
интеграл данной функции с двумя
бесконечными пределами интегрирования,
определяющийся формулой:
![]() ,
где с — произвольное число.
,
где с — произвольное число.
Геометрический смысл несобственного интеграла I рода
Несобственный интеграл первого рода выражает площадь бесконечно длинной криволинейной трапеции.
Примеры
![]()
Несобственные интегралы II рода
Пусть ![]() определена
на
определена
на ![]() ,
терпит бесконечный разрыв в точке x=a
и
,
терпит бесконечный разрыв в точке x=a
и ![]() .
Тогда:
.
Тогда:
Если
 ,
то используется обозначение
,
то используется обозначение  и
интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся.
и
интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся.Если
 или
или  ,
то обозначение сохраняется, а
,
то обозначение сохраняется, а  называется
расходящимся к
называется
расходящимся к  ,
или просто расходящимся.
,
или просто расходящимся.
Пусть ![]() определена
на
определена
на ![]() ,
терпит бесконечный разрыв при x=b и
,
терпит бесконечный разрыв при x=b и ![]() .
Тогда:
.
Тогда:
Если
 ,
то используется обозначение
,
то используется обозначение  и
интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся.
и
интеграл называется несобственным
интегралом Римана второго рода.
В этом случае интеграл называется
сходящимся.Если
 или
или  ,
то обозначение сохраняется, а
,
то обозначение сохраняется, а  называется
расходящимся к
называется
расходящимся к  ,
или просто расходящимся.
,
или просто расходящимся.
Если
функция ![]() терпит
разрыв во внутренней точке
терпит
разрыв во внутренней точке ![]() отрезка
отрезка ![]() ,
то несобственный интеграл второго рода
определяется формулой:
,
то несобственный интеграл второго рода
определяется формулой:
![]()
Геометрический смысл несобственных интегралов II рода
Несобственный интеграл второго рода выражает площадь бесконечно высокой криволинейной трапеции
Пример

Отдельный случай
Пусть
функция ![]() определена
на всей числовой оси и имеет разрыв в
точках
определена
на всей числовой оси и имеет разрыв в
точках ![]() .
.
Тогда
можно найти несобственный интеграл ![]()
признак
сходимости Абеля:
![]() 1.
пусть функции f(x) и g(x) определены
в промежутке
1.
пусть функции f(x) и g(x) определены
в промежутке ![]() ,
причём f(x) интегрируема
в этом промежутке, т.е. интеграл
,
причём f(x) интегрируема
в этом промежутке, т.е. интеграл  сходится
(условно или абсолютно);
сходится
(условно или абсолютно);
![]() 2. g(x) монотонна
и ограничена:
2. g(x) монотонна
и ограничена: ![]() .
Тогда
интеграл
.
Тогда
интеграл  сходится.
сходится.
![]() признак
сходимости Дирихле:
признак
сходимости Дирихле:
![]() 1.
пусть функция f(x) интегрируема
в любом конечном промежутке [a, b],
и интеграл по этому промежутку ограничен
(как функция верхнего
предела b):
1.
пусть функция f(x) интегрируема
в любом конечном промежутке [a, b],
и интеграл по этому промежутку ограничен
(как функция верхнего
предела b):  ;
;
![]() 2. g(x) монотонно
стремится к нулю при
2. g(x) монотонно
стремится к нулю при ![]() :
: ![]() .
Тогда
интеграл
.
Тогда
интеграл  сходится.
сходится.
![]() Применим,
например, признак Дирихле к
Применим,
например, признак Дирихле к  . Здесь f(x)
= cos x, g(x)
= 1/x, условия
признака выполнены, поэтому интеграл
сходится условно.
. Здесь f(x)
= cos x, g(x)
= 1/x, условия
признака выполнены, поэтому интеграл
сходится условно.
2



Принцип обобщенной индукции
Пусть X – вполне упорядоченное относительно < множество, а S(х) – некоторое высказывание, касающееся элемента х из X. Если требуется доказать справедливость S(х) для всех х, принадлежащих X, то необходимо:
1) доказать, что справедливо S(х0), где х0 – наименьший элемент в X;
2) доказать для всех х в X, удовлетворяющих условию х0 < х, что если справедливо S (у) для всех у < х, то справедливо и S(х).
Отметим, что если X – множество положительных целых чисел, а отношение < имеет обычный смысл, то принцип обобщенной индукции идентичен принципу строгой индукции
Чтобы убедиться в действенности принципа обобщенной индукции как метода доказательства, предположим, что S(х) – некоторое высказывание, для которого уже доказаны оба положения. Мы хотим сделать вывод о том, что S(х) справедливо для любых х в X. Предположим, что это не так. Пусть множество А = {х : х принадлежит X и S(х) ложно}. Если S(х) не справедливо для всех х в X, то А – непустое подмножество X. Так как X вполне упорядочено, то известно, что А содержит наименьший элемент а0. По определению это наименьший элемент X, для которого S(х) не справедливо. Таким образом, S(у) справедливо для всех у (если они есть), удовлетворяющих условию у < а0. Если а0 – наименьший элемент в X, то S(а0) справедливо, что следует из первого положения. В противном случае из справедливости S(у) для всех у < а0 и второго положения вытекает, что S(а0) справедливо. Но это противоречит предположению, что а0 принадлежит А и S(а0) ложно. Единственный способ устранить это противоречие – считать А пустым множеством, т.е. в X нет элементов, для которых высказывание S(х) ложно.
