1. Определенный интеграл

Пусть функция  определена на отрезке , .

Разобьем отрезок  точками  на n частичных отрезков  ; в каждом из частичных отрезков ,  выберем произвольную точку  и вычислим значение функции в этой точке: ; найдем произведения , где  – длина частичного отрезка , ; составим сумму

, (1)

которая называется интегральной суммой функции y = f(x) на отрезке[а, b]. С геометрической точки зрения интегральная сумма  представляет собой сумму площадей прямоугольников, основаниями которых являются частичные отрезки , а высоты равны  соответственно (рис. 1). Обозначим через  длину наибольшего частичного отрезка;найдем предел интегральной суммы, когда .

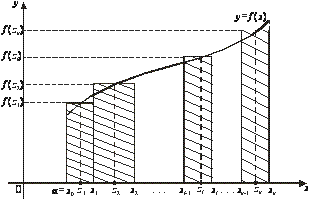
Рис. 1

Определение. Если существует конечный предел интегральной суммы (1) и он не зависит ни от способа разбиения отрезка  на частичные отрезки, ни от выбора точек  в них, то этот предел называется определенным интегралом от функции  на отрезке  и обозначается .

Таким образом, .

В этом случае функция  называется интегрируемой на . Числа а и b называются соответственно нижним и верхним пределами интегрирования,  – подынтегральной функцией,  – подынтегральным выражением,  – переменной интегрирования; отрезок  называется промежутком интегрирования.

Теорема 1. Если функция  непрерывна на отрезке , то она интегрируема на этом отрезке.

Геометрический смысл определенного интеграла

Пусть на отрезке  задана непрерывная неотрицательная функция . Криволинейной трапецией называется фигура, ограниченная сверху графиком функции y = f(x), снизу – осью Ох, слева и справа – прямыми x = a и x = b (рис. 2).

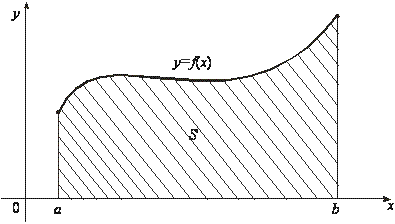
Рис. 2

Определенный интеграл 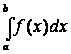 от неотрицательной функции  с геометрической точки зрения численно равен площади криволинейной трапеции, ограниченной сверху графиком функции , слева и справа – отрезками прямых  и , снизу – отрезком  оси Ох.

Свойства определённого интеграла

        Свойство 1. Производная от определённого интеграла по верхнему пределу равна подынтегральной функции, в которую вместо переменной интегрирования подставлено значение верхнего предела. То есть 

        Свойство 2. Определённый интеграл от суммы функций равен сумме неопределённых интегралов 

        Свойство 3. Постоянный множитель можно выносить за знак определённого интеграла 

        Свойство 4. Если на отрезке     , где, функциииудовлетворяют условию, то

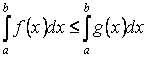        Свойство 5. Если     и- наименьшее и наибольшее значения функциина отрезкеи, то

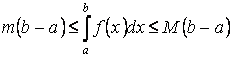        Свойство 6. Если поменять местами верхний и нижний пределы интегрирования, то определённый интеграл изменит знак 

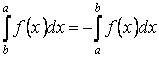      Свойство 7. Для любых трёх чисел     справедливо равенство

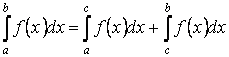если только все три интеграла существуют.          Свойство 8 (Теорема о среднем). Если функция     непрерывна на отрезке, то на этом отрезке найдётся такая точка, что справедливо равенство:

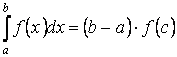
Суммы Дарбу и их свойства.Пусть функция , определённая на отрезке , ограничена на этом отрезке и пусть - разбиение отрезка , (i=1,n). Обозначим, ,  , .                    (5) Назовём и соответственно верхней и нижней суммами Дарбу для функции при заданном разбиении отрезка . Заметим, что  эти суммы не зависят от выборки .Рассмотрим свойства сумм Дарбу.

                                                      С в о й с т в о  1.

   Для любой выборки  справедливы неравенства.                                                     (6) ○ Так как для любого , выполняются неравенстватоСкладывая эти неравенства, получаем   .                           (7) Согласно определению сумм Дарбу и интегральной суммы утверждения (7) и (6) равносильны.

                                                     С в о й с т в о  2.

Спараведливы равенства  ,        (8) .       (9) ○ Докажем утверждение (8). Согласно определению точной верхней грани нужно доказать, что выполняются следующие условия: . Первое из этих условий выполняется в силу (6). Докажем второе условие. Так как , то по определению точной верхней грани :. Умножая  -е неравенство на и складывая все полученные неравенства, находим  , Где - выборка. Итак, утверждение (8) доказано. Аналогично доказывается, что справедливо и утверждение (9).●Следующее свойство сумм Дарбу связано с ещё одним понятием для разбиений. Назовём разбиение  продолжением (измельчением) разбиения , если каждая точка разбиения является точкой разбиения . Иначе говоря, Разбиение либо совпадает с разбиением , либо получено из добавлением по крайней мере одной новой точки.                                           С в о й с т в о  3.

Если разбиение  -  продолжение разбиения , то(10) т.е. при измельчении разбиения нижняя сумма Дарбу не уменьшается, а верхняя не увеличивается. ○ Для доказательства неравенств (10) достаточно рассмотреть случай, когда разбиение получается из разбиения добавлением только одной точки . пусть и - отрезки, на которые точка разбивает отрезок , а и - длины этих отрезков; тогда . Обозначим , . Очевидно, что , . В суммах и равны все соответствующие слагаемые, за исключением тех, которые связаны с отрезком . Поэтому+ ,  где  , . Следовательно,+ , т.е.  . Аналогично доказывается неравенство . Отсюда, используя неравенство (см.(6)), получаем цепочку неравенств (10).

                                            С в о й с т в о  4.

Для любых разбиений и справедливо неравенство         (11) ○ Пусть разбиение  является продолжением как разбиения , так и  разбиения (в качестве можно взять и добавить к нему те точки разбиения , которые не входят в ). Из неравенств (10) при , получаем. Полагая в (10) = и = , находим . Объединяя полученные неравенства, имеем, Откуда следует неравенство (11).●

                                              С в о й с т в о  5.

Существуют числа  , Удовлетворяющие для любых разбиений и отрезка условию (12) Эти числа называют соответственно нижним и верхним интегралами Дарбу от функции на отрезке . ○ Из неравенства (11) по теореме об отделимости числовых множеств следует, что существует и (супремум и инфимум по всевозможным разбиениям отрезка и для любых разбиений и выполняется неравенство (12).● свойства 1-5 справедливы для любой ограниченной на отрезке функции.

Критерий интегрируемости функции

Полезным для дальнейшего является понятие колебания функции  на отрезке : 

В частности, 

Следовательно,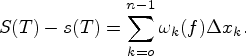 

Сформулируем необходимое и достаточное условие интегрируемости функции на отрезке .

Теорема 1 (критерий Римана). Для того чтобы ограниченная функция  была интегрируемой на отрезке , необходимо и достаточно, чтобы для любого  нашлось такое разбиение  отрезка , при котором или 

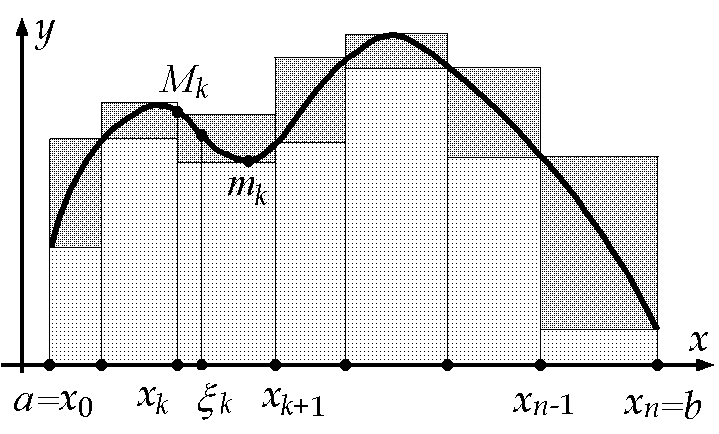
Замечание 1. Из этого условия следует, что интегрируемость функции  равносильна тому, что для любого  найдется разбиение отрезка , при котором график функции  можно поместить в "змейку'', составленную из прямоугольников общей площади меньше  

Доказательство. Необходимость. Из определения интегрируемости функции  на  следует, что для любого  найдется  такое, что для всех разбиений , мелкость которых , и для всех выполняется условие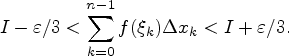 

Переходя к  и  в этих неравенствах по ,  и воспользовавшись свойством 1 сумм Дарбу, получим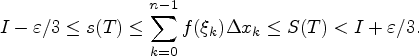 

Отсюда 

Достаточность. Пусть  произвольно и  -- такое разбиение отрезка , при котором . По свойствам  имеем

Отсюда, по условию теоремы,

Следовательно, ввиду произвольности , имеем

Докажем теперь, что функция  интегрируема на  и интеграл от нее равен числу . Возьмем произвольное  , тогда по лемме Дарбу существует  такое, что для любого разбиения  отрезка  мелкостью  выполняется 

В силу того, что для любого  

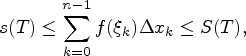
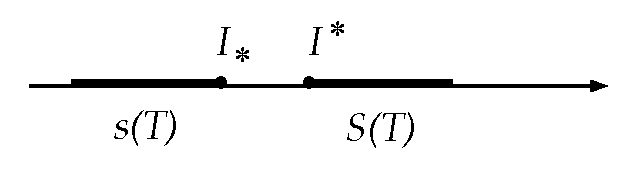
из неравенства (9.5.1) имеем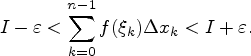 

Определённый интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий:

• Предел a или b (или оба предела) являются бесконечными;

• Функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a, b].