
Содержание
Задача № 1…………………………………………………………………………5
Задача № 2…………………………………………………………………………9
Задача № 3………………………………………………………………………..12
Задача № 4………………………………………………………………………..13
Основная часть
Задача № 1
По приводимым ниже данным рассчитать линейное регрессионное уравнение связи между годовым объёмом валовой продукции, приходящимся в среднем на одно предприятие, и размерами предприятий по стоимости основных фондов (млн. руб.):
|
|
Группы основных предприятий фондов по размеру (млн. руб.) |
|
|||
|
|
0,5 - 3,5 |
3,5 - 6,5 |
6,5 - 9,5 |
9,5 - 12,5 |
Итого |
|
Годовой объём валовой продукции на одно предприятие (млн. руб.) |
2,2 |
8,8 |
10,1 |
16,2 |
6,0 |
|
Число предприятий |
14 |
4 |
5 |
2 |
25 |
Решение:
Графический метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают значения результативного признака Y, а по оси абсцисс - факторного признака X.
Совокупность точек результативного и факторного признаков называется полем корреляции.
На основании поля корреляции можно выдвинуть гипотезу о том, что связь между всеми возможными значениями X и Y носит линейный характер.
Линейное уравнение регрессии имеет вид y = bx + a + ε
Здесь ε - случайная ошибка (отклонение, возмущение). Так как отклонения εi для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то по наблюдениям xi и yi можно получить только оценки параметров α и β.
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где ei – наблюдаемые значения (оценки) ошибок εi, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β - используют МНК (метод наименьших квадратов). Метод наименьших квадратов дает наилучшие оценки параметров уравнения регрессии, если выполняются определенные предпосылки относительно случайного члена (ε) и переменной (x).
Критерий МНК можно записать так:
S = ∑(yi - y*i)2 → min
Система нормальных уравнений.
a•n + b∑x = ∑y
a∑x + b∑x2 = ∑y•x
Для решения возьмём средние значения основных фондов предприятий.
0,5 - 3,5 млн. руб. – 2 млн. руб.
3,5 - 6,5 млн. руб. – 5 млн. руб.
6,5 - 9,5 млн. руб. – 8 млн. руб.
9,5 – 12,5млн. руб. – 11 млн. руб.
Для данных система уравнений имеет вид:
4a + 26 b = 37.3
26 a + 214 b = 307.4
Из первого уравнения выражаем а и подставим во второе уравнение:
Получаем коэффициенты регрессии: b = 1.44, a = -0.0567
Уравнение регрессии:
y = 1.44 x - 0.0567
1. Параметры уравнения регрессии.
Выборочные средние.
Выборочные дисперсии:
Среднеквадратическое отклонение
-
Коэффициент корреляции (Ковариация)
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными. Их критерии оцениваются по шкале Чеддока:
0.1 < rxy < 0.3: слабая;
0.3 < rxy < 0.5: умеренная;
0.5 < rxy < 0.7: заметная;
0.7 < rxy < 0.9: высокая;
0.9 < rxy < 1: весьма высокая;
В нашем примере связь между признаком Y фактором X весьма высокая и прямая.
1.2. Уравнение регрессии (оценка уравнения регрессии)
Линейное уравнение регрессии имеет вид y = 1.44 x -0.0567
Коэффициентам уравнения линейной регрессии можно придать экономический смысл.
Коэффициент регрессии b = 1.44 показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y повышается в среднем на 1.44.
Коэффициент a = -0.0567 формально показывает прогнозируемый уровень у, но только в том случае, если х=0 находится близко с выборочными значениями.
Подставив в уравнение регрессии соответствующие значения х, можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения.
Связь между у и х определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе - обратная). В нашем примере связь прямая.
1.3. Коэффициент эластичности
Средний коэффициент эластичности E показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения.
Коэффициент эластичности находится по формуле:
В нашем примере коэффициент эластичности больше 1. Следовательно, при изменении Х на 1%, Y изменится более чем на 1%, Х существенно влияет на Y.
Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном значении остальных независимых переменных:
т.е. увеличение x на величину среднеквадратического отклонения Sx приведет к увеличению среднего значения Y на 0.97 среднеквадратичного отклонения Sy.
1.4. Ошибка аппроксимации.
Средняя ошибка аппроксимации - среднее отклонение расчетных значений от фактических:
Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем подборе уравнения регрессии к исходным данным.
Поскольку ошибка больше 7%, то данное уравнение не желательно использовать в качестве регрессии.
1.5. Эмпирическое корреляционное отношение
Эмпирическое корреляционное отношение вычисляется для всех форм связи и служит для измерение тесноты зависимости. Изменяется в пределах [0;1].
где
Индекс корреляции.
Для линейной регрессии индекс корреляции равен коэффициенту корреляции rxy = 0.9736.
Полученная величина свидетельствует о том, что фактор x существенно влияет на y.
Для любой формы зависимости теснота связи определяется с помощью множественного коэффициента корреляции:
Данный коэффициент отражает тесноту связи и точность модели, может использоваться при любой форме связи переменных. При построении однофакторной корреляционной модели коэффициент множественной корреляции равен коэффициенту парной корреляции rxy. В отличие от линейного коэффициента корреляции он характеризует тесноту нелинейной связи и не характеризует ее направление. Изменяется в пределах [0;1].
1.6. Коэффициент детерминации
Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.
R2= 0.97362 = 0.9478
т.е. в 94.78 % случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - высокая. Остальные 5.22 % изменения Y объясняются факторами, не учтенными в модели.
|
x |
y |
x 2 |
y 2 |
x • y |
y(x) |
(yi-ycp) 2 |
(y-y(x))2 |
(xi-xcp)2 |
|y - yx|:y |
|
2 |
2.2 |
4 |
4.84 |
4.4 |
2.83 |
50.77 |
0.4 |
20.25 |
0.29 |
|
5 |
8.8 |
25 |
77.44 |
44 |
7.16 |
0.28 |
2.69 |
2.25 |
0.19 |
|
8 |
10.1 |
64 |
102.01 |
80.8 |
11.49 |
0.6 |
1.93 |
2.25 |
0.14 |
|
11 |
16.2 |
121 |
262.44 |
178.2 |
15.82 |
47.27 |
0.14 |
20.25 |
0.0235 |
|
26 |
37.3 |
214 |
446.73 |
307.4 |
37.3 |
98.91 |
5.16 |
45 |
0.63 |
Задача № 2
Используя критерии Вальда, Сэвиджа, Гурвица ( = 0,5), найти оптимальные стратегии, соответствующие каждому из критериев для игры, представляемой матрицей:
5 2 8 4
С
=
2 3 4 12
8 5 3 10
1 4 2 8 .
Решение:
Критерий Вальда:
По критерию Вальда за оптимальную принимается чистая стратегия, которая в наихудших условиях гарантирует максимальный выигрыш, т.е.
a = max(min aij)
Критерий Вальда ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации.
|
Ai |
П1 |
П2 |
П3 |
П4 |
min(aij) |
|
A1 |
5 |
2 |
8 |
4 |
2 |
|
A2 |
2 |
3 |
4 |
12 |
2 |
|
A3 |
8 |
5 |
3 |
10 |
3 |
|
A4 |
1 |
4 |
2 |
8 |
1 |
Выбираем из (2; 2; 3; 1) максимальный элемент max=3
Вывод: выбираем стратегию N=3.
Критерий Севиджа:
Критерий минимального риска Севиджа рекомендует выбирать в качестве оптимальной стратегии ту, при которой величина максимального риска минимизируется в наихудших условиях, т.е. обеспечивается:
a = min(max rij)
Критерий Сэвиджа ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации.
Находим матрицу рисков.
Риск – мера несоответствия между разными возможными результатами принятия определенных стратегий. Максимальный выигрыш в j-м столбце bj = max(aij) характеризует благоприятность состояния природы.
1. Рассчитываем 1-й столбец матрицы рисков.
r11 = 8 - 5 = 3; r21 = 8 - 2 = 6; r31 = 8 - 8 = 0; r41 = 8 - 1 = 7;
2. Рассчитываем 2-й столбец матрицы рисков.
r12 = 5 - 2 = 3; r22 = 5 - 3 = 2; r32 = 5 - 5 = 0; r42 = 5 - 4 = 1;
3. Рассчитываем 3-й столбец матрицы рисков.
r13 = 8 - 8 = 0; r23 = 8 - 4 = 4; r33 = 8 - 3 = 5; r43 = 8 - 2 = 6;
4. Рассчитываем 4-й столбец матрицы рисков.
r14 = 12 - 4 = 8; r24 = 12 - 12 = 0; r34 = 12 - 10 = 2; r44 = 12 - 8 = 4;
|
Ai |
П1 |
П2 |
П3 |
П4 |
|
A1 |
3 |
3 |
0 |
8 |
|
A2 |
6 |
2 |
4 |
0 |
|
A3 |
0 |
0 |
5 |
2 |
|
A4 |
7 |
1 |
6 |
4 |
Результаты вычислений оформим в виде таблицы.
|
Ai |
П1 |
П2 |
П3 |
П4 |
max(aij) |
|
A1 |
3 |
3 |
0 |
8 |
8 |
|
A2 |
6 |
2 |
4 |
0 |
6 |
|
A3 |
0 |
0 |
5 |
2 |
5 |
|
A4 |
7 |
1 |
6 |
4 |
7 |
Выбираем из (8; 6; 5; 7) минимальный элемент min=5
Вывод: выбираем стратегию N=3.
Критерий Гурвица:
Критерий Гурвица является критерием пессимизма - оптимизма. За (оптимальную принимается та стратегия, для которой выполняется соотношение:
max(si)
где si = y min(aij) + (1-y)max(aij)
При y = 1 получим критерий Вальде, при y = 0 получим – оптимистический критерий (максимакс).
Критерий Гурвица учитывает возможность как наихудшего, так и наилучшего для человека поведения природы. Как выбирается y? Чем хуже последствия ошибочных решений, тем больше желание застраховаться от ошибок, тем y ближе к 1.
Рассчитываем si.
s1 = 0.5•2+(1-0.5)•8 = 5
s2 = 0.5•2+(1-0.5)•12 = 7
s3 = 0.5•3+(1-0.5)•10 = 6.5
s4 = 0.5•1+(1-0.5)•8 = 4.5
|
Ai |
П1 |
П2 |
П3 |
П4 |
min(aij) |
max(aij) |
y min(aij) + (1-y)max(aij) |
|
A1 |
5 |
2 |
8 |
4 |
2 |
8 |
5 |
|
A2 |
2 |
3 |
4 |
12 |
2 |
12 |
7 |
|
A3 |
8 |
5 |
3 |
10 |
3 |
10 |
6.5 |
|
A4 |
1 |
4 |
2 |
8 |
1 |
8 |
4.5 |
Выбираем из (5; 7; 6.5; 4.5) максимальный элемент max=7
Вывод: выбираем стратегию N=2.
Таким образом, в результате решения статистической игры по различным критериям чаще других рекомендовалась стратегия A3.
Задача № 3
Определить размер оптимальной партии заказа, оптимальное число поставок в год, оптимальный интервал между поставками и средний уровень текущего запаса при следующих условиях: затраты на организацию заказа равны С1 = 6 тыс. рублей, а на хранение единицы продукции в запасе в течение года - С2 = 480 рублей. Общий расход продукции за год Q = 2500 единиц.
Решение:
Размер оптимальной партии заказа рассчитаем по формуле Уилсона:
Sопт. = √2*О*Ст/Сх, где
Sопт. - размер оптимальной партии;
О - величина оборота;
Ст - затраты на организацию заказа (транспортировку);
Сх - затраты на хранение продукции.
Sопт. = √2*2500 шт.*6000 руб./480 руб.
Sопт. =√62500 = 250 шт.
Оптимальное число поставок в год рассчитаем по формуле:
N=О/ Sопт., где
N - оптимальное число поставок в год.
N = 2500 шт./250 шт. = 10.
Оптимальный интервал между поставками найдём по формуле:
I = 365 дн./N, где
I - оптимальный интервал между поставками.
I = 365 дн. /10 = примерно 36 дн.
Средний уровень текущего запаса определим по формуле:
AIL = Q/2, где
AIL - средний уровень текущего запаса.
AIL = 250 шт./2 = 125 шт.
Задача № 4
На рис. приведён сетевой график. Продолжительность работ в днях указана рядом с графическим изображением каждой работы.
Необходимо:
1) Пронумеровать события.
2) Выделить критический путь и найти его длину.
3) Определить резервы времени каждого события.
4) Определить полные резервы времени некритических работ.
5) Определить коэффициенты напряжённости работ.
6) Построить линейный график сетевой модели.






 11 13
11 13
 5 10
5 10
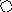
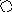



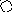


 6 11 17 25 14
6 11 17 25 14







32 12 13 9
8






21 7
Решение:
Все вычисления будем заносить в таблицу.
Перечень работ и их продолжительность перенесем во вторую и третью графы. При этом работы следует записывать в графу 2 последовательно: сначала начиная с номера 1, затем с номера 2 и т.д.
Во второй графе поставим число, характеризующее количество непосредственно предшествующих работ (КПР) тому событию, с которого начинается рассматриваемая работа.
Так, для работы (4,6) в графу 1 поставим число 2, т.к. на номер 4 оканчиваются 2 работы: (1,4),(2,4).
Далее заполняем графы 4 и 5. Для работ, имеющих цифру 0 в графе 2, в графу 4 также заносятся нули, а их значения в графе 5 получаются в результате суммирования граф 3 и 4.
Для заполнения следующих строк графы 4, т.е. строк начиная с номера 2, просматриваются заполненные строки графы 5, содержащие работы, которые оканчиваются на этот номер, и максимальное значение переносится в графу 4 обрабатываемых строк.
Этот процесс повторяется до тех пор, пока не будет заполнена последняя строка таблицы.
Заполнение графы 4:
Графы 6 и 7 заполняются обратным ходом, т.е. снизу вверх. Для этого просматриваются строки, оканчивающиеся на номер последнего события, и из графы 5 выбирается максимальная величина, которая записывается в графу 7 по всем строчкам, оканчивающимся на номер последнего события (т.к. tр(i)= tп(i)).
Процесс повторяется до тех пор, пока не будут заполнены все строчки по графам 6 и 7.
Заполнение графы 7:
Содержимое графы 8 равно разности граф 6 и 4 или граф 7 и 5.
|
Работа (i,j) |
Количество предшествующих работ |
Продолжительность tij |
Ранние сроки: начало tijР.Н. |
Ранние сроки: окончание tijР.О. |
Поздние сроки: начало tijП.Н. |
Поздние сроки:окончание tijП.О. |
Резервы времени: полный tijП |
Резервы времени: свободный tijС.В. |
Резервы времени: событий Rj |
|
(1,2) |
0 |
6 |
0 |
6 |
-72 |
-66 |
-72 |
0 |
-72 |
|
(1,4) |
0 |
8 |
0 |
8 |
-36 |
-28 |
-36 |
30 |
-66 |
|
(2,3) |
1 |
11 |
6 |
17 |
-66 |
-55 |
-72 |
0 |
-72 |
|
(2,4) |
1 |
32 |
6 |
38 |
-60 |
-28 |
-66 |
0 |
-66 |
|
(3,5) |
1 |
17 |
17 |
34 |
-55 |
-38 |
-72 |
0 |
-72 |
|
(4,6) |
2 |
21 |
38 |
59 |
-28 |
-7 |
-66 |
0 |
-66 |
|
(4,7) |
2 |
12 |
38 |
50 |
-25 |
-13 |
-63 |
9 |
-72 |
|
(5,7) |
1 |
25 |
34 |
59 |
-38 |
-13 |
-72 |
0 |
-72 |
|
(5,8) |
1 |
13 |
34 |
47 |
51 |
64 |
17 |
17 |
0 |
|
(6,9) |
1 |
7 |
59 |
66 |
-7 |
0 |
-66 |
-66 |
0 |
|
(7,8) |
2 |
5 |
59 |
64 |
59 |
64 |
0 |
0 |
0 |
|
(7,9) |
2 |
13 |
59 |
72 |
-13 |
0 |
-72 |
-72 |
0 |
|
(7,10) |
2 |
14 |
59 |
73 |
60 |
74 |
1 |
1 |
0 |
|
(8,10) |
2 |
10 |
64 |
74 |
64 |
74 |
0 |
0 |
0 |
1) графы 1 и 3 заполняются на основе исходных данных.
2) в графе 2 записывается количество предшествующих работ по сетевому графику или определяется из графы 1 по числу работ, имеющих второй цифрой в коде ту, с которой начинается данная работа.
3) в графе 4 раннее начало работ, выходящих из исходного события, а раннее окончание этих работ равно их продолжительности (гр. 5). Раннее начало последующих работ определяется путем выбора максимального из сроков раннего окончания предшествующих работ. Количество сравниваемых сроков равно количеству предшествующих работ графы 2. Раннее начало последующих работ можно определить после того, как найдено раннее окончание предшествующих. В свою очередь раннее окончание каждой работы находится как сумма величин раннего начала и продолжительности данной работы;
4) продолжительность критического пути определяется после заполнения граф 4 и 5 как максимальная величина из сроков раннего окончания работ, которые ведут к завершающему событию 9;
5) найденная величина критического пути ТKP дням заносится в графу 7 для всех работ, ведущих к завершающему событию. Затем заполнение ведется снизу вверх. Находятся все работы, следующие за рассматриваемой, и определяются разности между поздним окончанием этих работ и их продолжительностями. Минимальная из величин заносится в графу 7;
6) в графе 6 позднее начало работы определяется как разность позднего окончания этих работ и их продолжительности (из значений графы 7 вычитаются данные графы 3);
7) в графе 8 полный резерв времени работы определяется разностью между значениями граф 7 и 5. Если он равен нулю, то работа является критической;
8) в графе 10 резерв времени событий j определяется как разность позднего окончания работы, заканчивающегося событием j графы 7, и ранним началом работы, начинающимся событием j;
9) значение свободного резерва времени работы определяется как разность значений графы 10 и данных графы 8 и указывает на расположение резервов, необходимых для оптимизации.
Критический путь: (7,8)(8,10)
Продолжительность критического пути: 74.
