Вариант № 5
1. Найти коэффициент линейной корреляции между признаками X и Y, распределение которых даётся следующей таблицей:
|
Х |
1 |
2 |
3 |
4 |
5 |
mx |
|
1 |
2 |
- |
- |
- |
- |
2 |
|
2 |
1 |
1 |
2 |
- |
- |
4 |
|
3 |
- |
2 |
2 |
1 |
- |
5 |
|
4 |
- |
- |
- |
2 |
2 |
4 |
|
my |
3 |
3 |
4 |
3 |
2 |
15 |
Y2. Найти решение игры, заданной матрицей:
4 3
С = 2 4
0 5 графическим методом.
1 6
3. Даны 5 работ, выполняемых в системе, состоящей из двух станков. Затраты времени указаны в таблице. Требуется найти оптимальный (в смысле min Тобр.) порядок проведения этих работ.
|
Работы (в произвольной нумерации) |
I |
II |
III |
IV |
V |
|
Продолжительность выполнения на первом станке |
6 |
0 |
5 |
8 |
2 |
|
Продолжительность выполнения на втором станке |
3 |
2 |
4 |
6 |
1 |
4. На рис. приведён сетевой график. Продолжительность работ в днях указана рядом с графическим изображением каждой работы.
Необходимо:
1) Пронумеровать события.
2) Выделить критический путь и найти его длину.
3) Определить резервы времени каждого события.
4) Определить полные резервы времени некритических работ.
5) Построить линейный график сетевой модели.
9 14
8 9
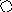
6 10 7 5 15
3 2 3 7
7
10 5
Вариант № 6
1. Пусть зависимость признака Y от признака Х характеризуется следующей таблицей:
|
Х |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Y |
0,5 |
0,5 |
1,5 |
3,5 |
6,5 |
10,5 |
15,5 |
Выровнять зависимость Y от Х по параболе у = ах2+ вх + с. Найти параметры этой зависимости, пользуясь методом наименьших квадратов.
2. Для матричной игры, заданной матрицей:
7 6 7 5
C
=
6 7 9 8
5 8 4 6 ,
записать соответствующую прямую и двойственную к ней задачу линейного программирования.
3. Определить размер оптимальной партии заказа, оптимальное число поставок в год, оптимальный интервал между поставками и средний уровень текущего запаса при следующих условиях: затраты на организацию заказа равны 60 тыс. руб., а на хранение единицы продукции в запасе в течение года - 520 руб. Общий расход продукции за год 1200 единиц.
4. На рис. приведён сетевой график. Продолжительность работ в днях указана рядом с графическим изображением каждой работы.
Необходимо:
1) Пронумеровать события.
2) Выделить критический путь и найти его длину.
3) Определить резервы времени каждого события.
4) Определить полные и свободные резервы времени некритических работ.
5) Построить линейный график сетевой модели.
25
8
9 10 3
6 12 4
5 4 8 18
1
4
16
15