
Вариант № 1
1. Пусть зависимость признака Y от признака Х характеризуется следующей таблицей:






 Х
2
1 0
1 2 3
Х
2
1 0
1 2 3

Y 2 3 3 1 3,5 8
Предполагая, что теоретически у = ах2 + bх + с, найти параметры этой зависимости, пользуясь методом наименьших квадратов.
2. Найти оптимальные стратегии игроков и цену игры, заданной матрицей:
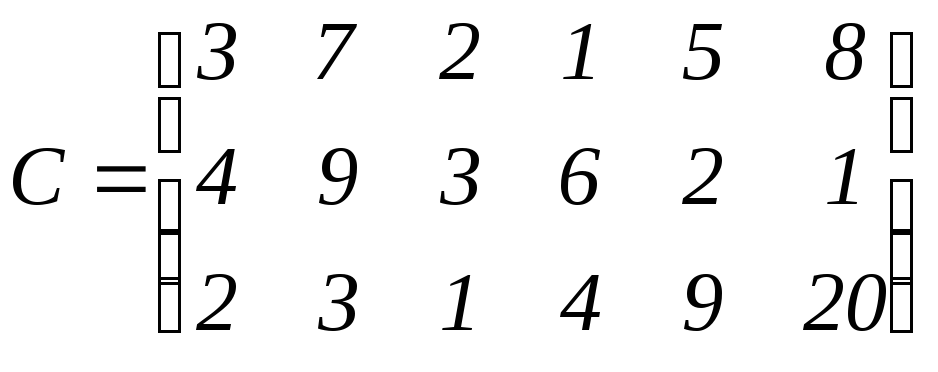
, пользуясь упрощением платёжной матрицы и приведя матрицу С к размеру, позволяющему решить задачу геометрически.
3. Требуется определить оптимальный размер поставки мелко-сортовой стали (пруток 12 мм) машиностроительному заводу при следующих условиях: годовая потребность - Q = 1000 тонн, условно-постоянные транспортно-заготовительные расходы на один заказ С1 = 550 рублей, издержки по содержанию запасов С2 = 400 рублей в год, потери из-за дефицита установлены исходя из необходимости замены прутка диаметром 12 мм прутком диаметром 14 мм, что составляет убыток 1350 рублей на тонну.
4. На рис. приведён сетевой график. Продолжительность работ в днях указана рядом с графическим изображением каждой работы.
Необходимо:
Пронумеровать события.
Выделить критический путь и найти его длину.
Определить резервы времени каждого события.
Определить полные резервы времени некритических работ.
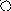
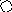
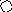
 5 6 9
5 6 9







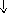 3
7 5
3
7 5
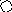
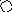
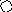


 5
3 5
5
3 5
 4
8 6
4
8 6
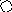
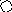
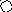
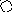



8 4 7
Вариант № 2
1. Пусть зависимость признака Y от признака Х характеризуется следующей таблицей:







 Х
1 2 3 4 5 6 7
Х
1 2 3 4 5 6 7

Y 0,5 0,5 1,5 3,5 6,5 10,5 15,5
Выровнять зависимость Y от Х по параболе у = ах2 + вх + с, т.е. найти а, в, с, пользуясь методом наименьших квадратов.
2. Найти решение игры, заданной матрицей:
![]() ,
т.е. найти оптимальные стратегии и
цену игры
,
т.е. найти оптимальные стратегии и
цену игры
3. Требуется определить оптимальный размер поставки мелко-сортовой стали (пруток 12 мм) машиностроительному заводу при следующих условиях: годовая потребность - Q = 550 тонн, условно-постоянные транспортно-заготовительные расходы на один заказ С1 = 375 рублей, издержки по содержанию запасов С2 = 255 рублей в год, потери из-за дефицита установлены исходя из необходимости замены прутка диаметром 12 мм прутком диаметром 14 мм, что составляет убыток 850 рублей на тонну.
4. На рис. приведён сетевой график. Продолжительность работ в днях указана рядом с графическим изображением каждой работы.
Необходимо:
1) Пронумеровать события.
2) Выделить критический путь и найти его длину.
3) Определить резервы времени каждого события.
4) Определить полные резервы времени некритических работ.
5) Построить линейный график сетевой модели.


 4
4




 7
7
8 6
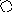
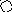

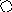
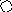
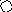 5 9 8 7 8
5 9 8 7 8










3 2 10 5 7
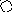


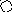


3 4
