Билет №5 Вопрос №2
Активные RC фильтры. Типы фильтров. Аппроксимация АЧХ ФНЧ. Фильтры Баттерворта и Чебышева.
Электрический фильтр представляет собой частотно-избирательное устройство, пропускающее сигналы в требуемой полосе частот, называемой полосой пропускания, и задерживающее сигналы других частот, относящихся к полосе задерживания. В зависимости от полосы частот прохождения сигнала фильтры с одной полосой пропускания классифицируются на фильтры нижних частот (ФНЧ), верхних частот (ФВЧ) и полосно-пропускающие (полосовые). Существуют и другие типы фильтров, такие, как всепропускающие, частотовыделяющие (узкополосные) и частотоподавляющие (режекторные). Другая классификация фильтров основана на тех положениях теории цепей, по которым они рассчитываются. Она включает фильтры по характеристическим параметрам и фильтры по рабочим параметрам. Также выделяют пассивные и активные фильтры. Примером пассивного фильтра является LC-фильтр, а примером активного –RC-фильтр.
Рассматриваемые активные RC-фильтры относятся к классу линейных электрических цепей с сосредоточенными и постоянными во времени параметрами.
Аппроксимация АЧХ – фильтров.
1)
- нормирование частоты
2)Норм. передачи:
M
1
Ω
1
Нужно перейти от
к самому коэффициенту. Для этого
приравниваем к 0 знаменатель и находим
корни. По ним восстанавливаем полиномы
Баттерворта.
Полиномы Баттерворта (сомножители
степени
)
|
n |
Сомножители |
|
1 |
(1+p) |
|
2 |
(1+1,4142p + p2) |
|
3 |
(1+p)(1+p+p2) |
|
4 |
(1+0,7654p+p2)(1+1,847p+p2) |
M1
M3 ,
Ω3
Чаще всего указывают не значение |M|,
а величинуa=-20lg(M)
,
По виду полинома, стоящего в знаменателе коэффициента передачи, различают фильтры Баттерворта, Чебышева, Весселя и др.
Фильтры Баттерворта, или фильтры с максимально плоской АЧХ
Этот фильтр во многих отношениях обеспечивает определённый компромисс. Он обладает максимально плоской АЧХ в полосе пропускания, но это достигается за счёт линейности ФЧХ и плавности нарастания затухания. Однако крутизна затухания фильтра Баттерворта достаточно хорошая, и поскольку он обладает приемлемой импульсной характеристикой, обеспечивает отличную универсальную аппроксимацию идеальной характеристики фильтра. Этот фильтр является одним из наиболее употребляемых типов фильтров.
Фильтры Чебышева.
Если же крутизна нарастания затухания, особенно в районе частоты среза, является более важным параметром, чем прямолинейность характеристики в полосе пропускания, то часто используется фильтр с характеристикой Чебышева. Он характеризуется возрастающей длительностью переходного процесса при воздействии на него ступенчатого сигнала и проектируется с заранее определённым размахом колебаний коэффициента передачи (т.е. равноволновым) в полосе пропускания, например от 0,01 до 3 дБ. Отсутствие гладкой характеристики в полосе пропускания дает определенные преимущества, а именно обеспечивается высокая скорость нарастания затухания вблизи края полосы пропускания. За исключением диапазона частот, вблизи полосы пропускания характеристическая кривая вне её идёт параллельно кривой характеристике фильтра Баттерворта эквивалентного порядка.
Существуют таблицы, как и для Баттерворта.
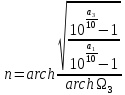
- Коэффициент передачи
в оп. форме.Максимальная степень полинома в знаменателе коэффициента передачи определяет порядок фильтра.
Скорость спада АЧХ за пред. Полосы пропускания nlg20
Как фильтры Баттерворта, так и фильтры Чебышева нижних частот обеспечивают бесконечное затухание только на бесконечной частоте, т.е. вес нули передачи расположены в бесконечности. На любой другой частоте некоторые сигналы будут проходить через фильтр, т.е. даже в полосе задерживания. Если же на неопределённой частоте в полосе задерживания требуется бесконечное подавление, то можно использовать характеристику инверсного фильтра Чебышева. В полосе пропускания колебания коэффициента передачи отсутствуют, но они существуют в полосе задерживания, и затухание на определённых частотах (так называемых полюсах затухания) становится бесконечным.